Провод, свёрнутый в форме спирали, называется катушкой (обмоткой). Катушка индуктивности по устройству напоминает обычную катушку ниток. Только в катушке индуктивности на сердечник (каркас) наматывают не нитки, а много витков изолированного провода.
Главным параметром катушки индуктивности является её индуктивность L. Повторите понятие "индуктивность", в разделе "Явление самоиндукции".
Термин “индуктивность”в электротехнике может означать:
1) параметр проводника (катушки), характеризующий его свойства в отношении величины наводимой в нём ЭДС самоиндукции;
2) собственно катушку, обладающую некоторой индуктивностью.
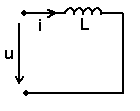
На рис. 51 показано условное графическое обозначение катушки индуктивности. К катушке приложено синусоидальное (переменное) напряжение U.
Рис. 51. Условное обозначение катушки индуктивности L. К катушке приложено переменное напряжение.
Катушкой индуктивности в электротехнике часто называют обмотку трансформатора или электродвигателя.
Через катушку индуктивности, показанную на рис. 51, проходит переменный ток I. Он создает вокруг катушки переменное магнитное поле. Это поле наводит в катушке ЭДС самоиндукции eL. Величина ЭДС самоиндукции, наводимой в катушке, зависит от индуктивности катушки L и скорости изменения тока в цепи 
I/ 
t.
В соответствии с правилом Ленца, ЭДС самоиндукции препятствует протеканию тока в цепи. Препятствие протеканию тока означает, что катушка индуктивности обладает сопротивлением, которое называется индуктивным.
Индуктивное сопротивление XL можно вычислить по формуле:
(Ом), где:
f - частота приложенного напряжения;
L - индуктивность катушки (Генри).
Из формулы следует, что индуктивное сопротивление зависит от частоты f приложенного напряжения. С увеличением частоты индуктивное сопротивление катушки увеличивается.
Ток в цепи катушки индуктивности можно определить по закону Ома:
При повышении частоты приложенного напряжения U индуктивное сопротивление растёт, а ток в цепи уменьшается.
Катушка индуктивности относится к классу реактивных элементов. К реактивным относятся элементы, в которых происходит обратимое преобразование энергии. В катушке периодически повторяются процессы накопления энергии в магнитном поле катушки и возвращении накопленной энергии генератору.
Мощность, выделяющаяся в катушке, называется реактивной и определяется по формуле:
,
где "вар" – вольт-ампер реактивный.
Ток в катушке не совпадает по фазе с напряжением, приложенным к ней. Ток отстает от напряжения по фазе на угол π/2 рад (90 градусов).
Рис. 52. Ток в катушке индуктивности отстаёт по фазе от напряжения
Пример 11. Идеальная индуктивность в цепи синусоидального тока
В сеть с действующим значением напряжения 120В частотой f = 50 Гц включена катушка с индуктивностью L= 127 мГн. Определить ток, протекающий через катушку и выделяющуюся в ней реактивную мощность.
Решение.
Идеальная катушка индуктивности обладает только одним параметром – индуктивностью L. Активное сопротивление провода, которым она намотана, не учитывается.
Индуктивность катушки приведена в условии задачи в миллигенри (мГн). В расчётных формулах следует все величины выражать в основной размерности. Поэтому, переведём индуктивность из миллигенри в генри. Приставка "милли" означает одну тысячную долю
127 мГн = 127/1000 Гн = 0,127 Гн.
Индуктивное сопротивление катушки:
ХL=2pfL= 2p · 50 · 0,127 = 40 Ом.
Ток в катушке, по закону Ома:
I= U/XL = 120 /40 = 3 А.
В катушке выделяется реактивная мощность
Q=U · I =120 · 3 = 360 вар.
