Математическая запись синусоидальной величины

     Математически синусоидальное напряжение может быть записано в виде выражения:

Аналогичный вид имеет запись для синусоидального тока или ЭДС.

    Математическое выражение позволяет вычислить мгновенное значение синусоидальной величины в данный момент времени. Для вычисления нужно знать амплитудное значение синусоидальной величины U_m (или I_m), её угловую частоту ω и время t, прошедшее с начала периода.

    Если начальная фаза синусоиды не равна нулю, нужно дополнительно учесть величину угла ψ (пси) в радианах. См. рис. 44.

 

Графическое изображение синусоидальных величин.

Начальная фаза

Для анализа работы схем, работающих на переменном токе, часто используются графики и диаграммы. Синусоидальные величины можно изображать двумя способами:

1. на волновой диаграмме;

2. на векторной диаграмме.

    Волновые диаграммы называются так потому, что график синусоиды напоминает волну. Все графики синусоидального тока, которые вы видели ранее, относятся к этому типу.

    Волновые диаграммы строятся в прямоугольной системе координат. По вертикальной оси откладывается мгновенное значение тока, (или напряжения, или ЭДС). По горизонтальной оси откладывается фазовый угол ωt. Он показывает на какой угол в радианах повернется рамка генератора за время t.

    Вспомните, что полная синусоида генерируется за один оборот рамки генератора. Это соответствует углу поворота рамки на 360 градусов или 2π радиан. Таким образом, по горизонтальной оси, начало синусоиды соответствует углу в ноль радиан, а конец синусоиды – углу 2π радиан. Напомним, что число π=3,14.

    На рис. 43 показана волновая диаграмма для синусоидального тока. Здесь начало положительного полупериода синусоиды совпадает с началом координат.

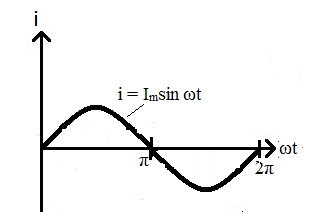
Рис. 43. Синусоидальная величина отображена на волновой диаграмме.

Начальная фаза синусоидальной величины равна нулю

 

    Не всегда начало синусоиды совпадает с началом координат. Чтобы учесть смещение начала синусоиды относительно начала координат, вводят понятие начальной фазы.

    Начальной фазой называется угол ψ (пси), на который начало синусоиды смещено относительно начала координат. На рис. 43 начальная фаза равна нулю. Синусоиды, для которых начальная фаза ψ не равна нулю, показаны на рис. 44.

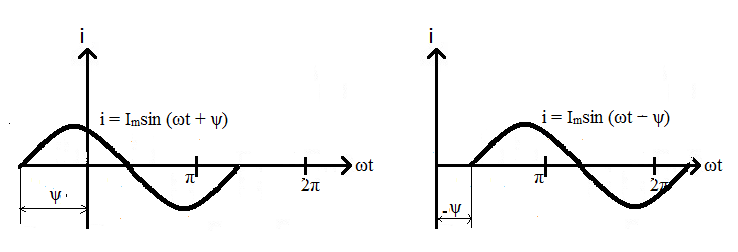
Рис. 44. Начальная фаза синусоиды не равна нулю

       Заметьте, что знак начальной фазы может быть как положительным, так и отрицательным. Это зависит от того, в какую сторону смещена синусоида, относительно начала координат.

    Запомните какой знак начальной фазы соответствует смещению синусоиды в каждую сторону.

    На графиках отображено математическое выражение для синусоиды., соответствующее графику. Видно, что в математическом выражении учитывается знак начальной фазы.

 

Векторные диаграммы

Синусоидальную величину можно изобразить вектором (рис. 45) в прямоугольной системе координат. На векторных диаграммах линии осей координат, обычно, не изображаются, а лишь подразумеваются. На рис. 46, для лучшего понимания, оси координат X и Y показаны. В дальнейшем они отображены не будут.

Рис. 45. Вектор

Длина вектора в масштабе пропорциональна действующему или амплитудному значению.

Вектор на диаграмме обозначается буквой (I, U или E). Буква ставится вблизи стрелки вектора.

При построении векторной диаграммы обязательно указывается масштаб, как показано на рис. 45. На рис. 45 показано, что один сантиметр длины вектора соответствует десяти вольтам. Масштаб всегда указывается на 1 сантиметр. Цифра выбирается произвольной, но всегда «круглой», например 20 или 50. Недопустимо значение, скажем 37,2В в 1см. Длину вектора в см. можно узнать разделив значение напряжения или тока, полученное в расчётах в на цифру масштаба.  

Векторы на диаграммах вращаются против часовой стрелки, вокруг своего начала, со скоростью ω. Направление вращения – против часовой стрелки.

Естественно, на рисунке векторы вращаться не могут. Сказанное о вращении векторов следует понимать следующим образом. На диаграмме векторы отображены для данного момента времени. В следующий момент времени их нужно отобразить повернувшимися на определённый угол по направлению вращения. Величина угла поворота соответствует скорости углу поворота рамки генератора, вырабатывающего электроэнергии.

 

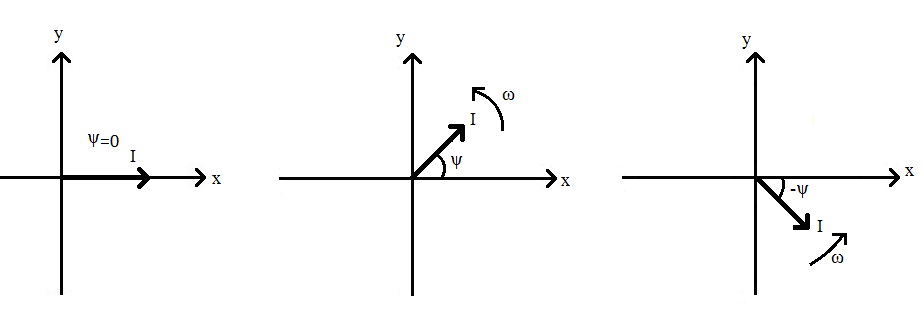
Рис. 46. Изображение токов в виде вектора

На рис. 46, в виде векторов, показаны синусоидальные величины с различной начальной фазой ψ. Начальная фаза векторов на рис. 46 соответствуют синусоидам на рисунках 43 и 44.

Сдвиг по фазе

 

Понятие сдвига по фазе возникает, если на одном графике отображаются сразу две синусоидальные величины, например два тока, два напряжения или же напряжение и ток. Понятие сдвига по фазе применяется только для синусоидальных величин одинаковой частоты.

Углом сдвига по фазе φ (фи) называется угол, на который смещены относительно друг друга начала двух синусоид. Значение угла фи может быть в интервале от нуля до π радиан (от нуля до180 градусов).

Две синусоидальные величины могут совпадать по фазе, не совпадать по фазе или находится в противофазе.

Сдвиг по фазе можно отобразить как на волновой, так и на векторной диаграмме. На рисунках 47, 48 и 49 показаны некоторые возможные случаи сдвига по фазе.

Синусоидальные величины совпадают по фазе. На рис. 47 токи i₁ и  i₂ совпадают по фазе. Это означает, что они начинаются в один момент и с течением времени изменяются синхронно: оба возрастают или оба уменьшаются. На векторной диаграмме оба вектора направлены в одну сторону. Угол φ сдвига по фазе между синусоидальными величинами равен нулю.

 

Рис. 47. Синусоидальные величины совпадают по фазе

 

    Синусоидальные величины не совпадают по фазе.  На рис. 48 показано, что токи i₁ и  i₂ не совпадают по фазе (смещены по фазе). Видно, что синусоиды токов начинаются в разные моменты времени. Угол сдвига по фазе φ (на данном графике) составляет π/2 радиан (90 градусов). Вспомним, что величина сдвига по фазе может находится в пределах от нуля до π радиан (от нуля до180 градусов).

    Можно сказать, что ток i₂ отстаёт по фазе от тока i₁ на угол π/2 радиан (90 градусов). Можно сказать и наоборот: ток i₁ опережает по фазе ток i₂ на угол π/2 радиан (90 градусов).

Рис. 48. Синусоидальные величины не совпадают по фазе

       На векторной диаграмме токи направлены друг к другу под углом φ.

 

    Синусоидальные величины находятся в противофазе.  На рис. 49 токи i₁ и  i₂ изменяются в противофазе. В момент, когда один ток проходит положительный полупериод, другой проходит отрицательный и наоборот. Если один ток нарастает со знаком плюс, то другой – со знаком минус.

    Угол φ сдвига по фазе между токами равен π радиан или 180 градусов. На векторной диаграмме противофазные векторы токов направлены в противоположные стороны.

Рис. 49. Синусоидальные величины изменяются в противофазе