3.1 Для оценки достижений студента используется
балльно-рейтинговая система:
· В каждом семестре студент должен выполнить домашнюю контрольную работу из двух частей. После её проверки студент получает баллы (рейтинг)
| Код | Вид оценочного средства | Максимальный балл | Зачтённая работа, баллы | Незачёт, баллы |
| Дз-3 Часть 1 | Домашняя контрольная работа (ДКР) | 20 | 11– 20 | 0 – 10 |
| Дз-3 Часть 2 | ДКР | 20 | 11– 20 | 0 – 10 |
| Э-2 | Экзамен | 60 | 26 – 60 | 0 – 25 |
· 
Допуском до экзамена является набранные за семестр 25 баллов при зачтённой каждой части контрольной работы. При недопуске студент исправляет ошибки в своей работе либо выполняет дополнительные задания для набора не менее 25 баллов;
· На экзамене в каждом билете имеется по 6 практических задач, каждая оценивается по 10 баллов, на их выполнение даётся 2 часа. Допускается использование дополнительной литературы. Для получения оценок 4 и 5 требуется ответить на несколько теоретических вопросов без применения литературы;
· При наборе на экзамене менее 26 баллов экзамен является несданным и выставляется неудовлетворительная оценка (независимо от набранных в семестре баллов);
· Оценкой за семестр является общий суммарный рейтинг в виде суммы баллов, накопленных за семестр, и полученных на экзамене. Оценка выставляется при наборе не менее 60 баллов с указанием этой суммы и соответствующей оценки.
| Оценка по 5 бальной шкале | Зачет | Сумма баллов по дисциплине | Оценка (ECTS) | Градация |
| 5 (отлично) | Зачтено | 90-100 | А | Отлично |
| 4 (хорошо) | 85-89 | В | Очень хорошо | |
| 75-84 | С | Хорошо | ||
| 70-74 |
D | Удовлетворительно | ||
| 3 (удовлетворительно) | 65-69 | |||
| 60-64 | Е | Посредственно | ||
| 2 (неудовлетворительно) | Не зачтено | Ниже 60 | F | Неудовлетворительно |
Вопросы экзамена
1. Область нескольких переменных, окрестность точки. Открытая и замкнутая области нескольких переменных. Функции нескольких переменных (ФНП): определение, способы задания. Геометрический смысл Z=f(x,y), линии уровня.
2. Предел ФНП в точке. Непрерывность ФНП в точке. Основные свойства непрерывных ФНП.
3. Определение частной производной ФНП, правила их вычисления. Геометрический смысл частных производных для Z=f(x,y). Уравнение касательной плоскости и нормали.
4. Полный дифференциал ФНП, связь с Δf, инвариантность его формы. Полная производная по переменной t. Производная неявной функции.
5. Производная по направлению. Градиент функции: определение, правила вычисления, связь с производной по направлению и с линией (поверхностью) уровня.
6. Частные производные высших порядков. Теорема о смешанных производных ФНП. Дифференциалы высших порядков для ФНП, их коэффициенты для f(x, y) (треугольник Паскаля и бином Ньютона). Формула Тейлора для ФНП. Приближенные вычисления.
7. Точки экстремума ФНП. Необходимое условие экстремума. Достаточное условие экстремума в общем виде и для f(x, y), характер экстремума.
8. Условный экстремум ФНП. Метод множителей Лагранжа и метод подстановки.
9. Нахождение наибольшего и наименьшего значений ФНП в замкнутой ограниченной области (план).
10. Общие понятия теории обыкновенных дифференциальных уравнений (ДУ): ДУ, его решение, общее и частное решения, начальные и краевые условия, интегральная кривая, задача Коши. Теорема Коши для ДУ первого порядка.
11. ДУ с разделенными и разделяющимися переменными, их решения. Сведение текстовой задачи к решению ДУ на примере задачи о распаде радия и о непрерывном растворении соли (или другой задачи).
12. Однородные функции двух переменных. Общий вид и правило интегрирования однородных диф. уравнений. Уравнения, приводящиеся к однородным, их интегрирование.
13. Линейные ДУ первого порядка, методы Бернулли и Лагранжа для их интегрирования.
14. Уравнение Бернулли, его интегрирование непосредственно и сведением к линейному ДУ.
15. Уравнение в полных дифференциалах: общий вид, правило интегрирования и физический смысл (потенциальность плоского векторного поля).
16. Методы Эйлера и изоклин приближенного построения интегральных кривых.
17. Решение ДУ в виде степенного ряда, два способа нахождения его коэффициентов;
18. ДУ второго порядка. Случаи ДУ, допускающих понижение порядка.
19. Линейное ДУ второго порядка: общий вид, свойства решений, структура общего решения.
20. Линейная зависимость системы функций. Определитель Вронского. Теорема о связи определителя Вронского с линейной зависимостью решений линейного однородного ДУ. Фундаментальная система решений и общее решение при этом.
21. Линейное однородное ДУ с постоянными коэффициентами: общий вид, метод Эйлера его решения, характеристическое уравнение. Общее решение линейного ДУ при известных корнях характеристического уравнения:
а) корни действительные, различные;
б) корни кратные;
в) корни комплексные, сопряженные.
22. Нахождение частного решения линейного неоднородного ДУ при неоднородности специального вида (метод подбора):
а) Pn (x); б) Pn (x). eax;в) eax . (Acos (bx) + Bsin (bx)); г) Сумма функций.
Нахождение коэффициентов предполагаемого решения.
23. Нахождение частного решения линейного неоднородного ДУ методом вариации постоянных.
24. ДУ, описывающее механические колебания. Случаи свободных, затухающих, вынужденных колебаний. Случай резонанса.
25. Каноническая и нормальная формы системы ДУ. Решение системы ДУ, общее и частное решения. Начальные условия. Теорема о существовании и единственности решения системы ДУ.
26. Сведение ДУ к системе ДУ в нормальной форме, системы ДУ к одному дифференциальному уравнению (метод исключения).
27. Системы линейных уравнений, свойства решений однородных систем и неоднородных систем ДУ. Определитель Вронского системы ДУ, его свойства. ФСР системы ЛОДУ.
28. Нахождение решений линейной однородной системы методом исключения.
29. Нахождение решений линейной однородной системы с помощью собственных векторов.
30. Нахождение решений линейной неоднородной однородной системы методом вариации постоянных.
3.3ПРИМЕР ЭКЗАМЕНАЦИОННОГО БИЛЕТА 
Справочник
· Интеграл является несобственным первого рода (НИ1), если f (x) непрерывна и хотя бы один из частичных пределов на концах промежутка интегрирования бесконечен;
· От непрерывной функции f (x) НИ1 вида 
сходится, если существует конечный предел 
;
· Необходимое условие сходимости НИ1: 
.
Из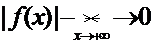 
следует расходимость ряда;
· Если 
, то
А) Из сходимости следует сходимость 
;
Б) Из расходимости следует расходимость ;
· Если 
, то и сходятся либо расходятся одновременно;
· Если 
, то сходится при 
, при 
он расходится;
· Если интеграл сходится и сходится 
, то сходимость абсолютная; при расходимости сходимость исходного интеграла условная;
· Для несобственного интеграла второго рода (НИ2)функция f (x) имеет на отрезке интегрирования точки, где её предел бесконечен либо не существует;
· НИ2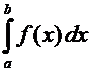 
с одной особой точкой х=а сходится, если существует конечный предел 
;
· Если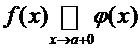 
, то и сходятся либо расходятся одновременно;
· Если 
, то НИ2 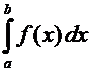сходится при 
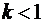, при 
он расходится;
· Числовой ряд 
,
− частичная сумма ряда;
· Если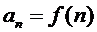 
− общий член ряда, то записывают 
, 
;
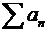· Ряд сходится, если существует конечное число 
,
тогда S− сумма ряда, 
;
· Геометрическая прогрессия со знаменателем q 
,
она сходится только при 
,
её частичная сумма 
даёт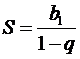 
;
· Необходимое условие сходимости 
.
Из 
следует расходимость ряда;
· Для знакоположительных рядов (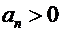
) выполнено
1) Признак Даламбера: если существует 
,
то 
;
2) Признак Коши (радикальный): если существует 
,
то 
;
Напоминание: 
;
3) Интегральный признак: Если найдётся непрерывная функция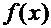 
, что выполнено 
, то числовой ряд 
и несобственный интеграл 
одновременно сходятся либо одновременно расходятся;
4) Признак эквивалентности: Эквивалентные знакоположительные ряды одновременно сходятся либо одновременно расходятся. Если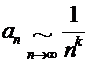 
, то при 
ряд сходится, при 
ряд расходится;
· Знакопеременный ряд сходится абсолютно, если ряд сходится и сходится ряд 
. Если сходится, но ряд расходится, то ряд сходится условно и можно подобрать перестановку и (или) группировку его элементов, при которой сумма ряда станет заданным произвольно числом;
· Теорема Лейбница: Если 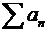знакочередующийся,
То А) При выполнении ряд сходится;
Б) Для сходящегося ряда выполнено 
;
В) Знак разности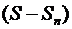 
совпадает со знаком числа 
;
· Функциональный ряд 
является степенным с центром сходимости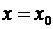 
. Внутри интервала сходимости 
он сходится и вне такого интервала расходится.
· Радиус сходимости степенного ряда
а) 
; б)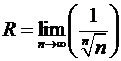 
;
· Ряд Тейлора 
, где 
;
· Основные разложения Маклорена в степенной ряд (
):
1) 
;
2) 
;
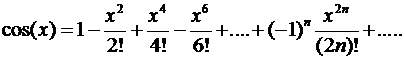3) 
;
4) 
;
5) 
· Теорема Коши: Если дифференциальное уравнение (ДУ) имеет вид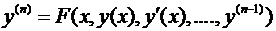 
, где F непрерывная функция и в некоторой области существуют и конечны производные 
,
ТО для всякого начального условия из такой области найдётся решение ДУ и такое решение единственно;
· ДУ с разделяющимися переменными, если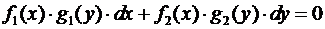 
, для него общий интеграл 
, частный интеграл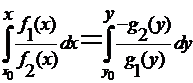 
;
· Функция однороднаяизмерения k, если 
. При однородности нулевого измерения 
;
· Однородное ДУ имеет вид 
, где 
однородные одинакового измерения. Его можно представить в виде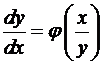 
.
Выполнив замену 
, получим
уравнение с разделяющимися переменными, в его общем решении
или в общем интеграле выполняется обратная замена;
· Линейное ДУ 
. Метод Бернулли: ищем решение в виде 
и требуем выполнения 
т.е. 
, тогда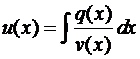 
;
· Уравнение Бернулли 
. Уравнение интегрируется методом Бернулли либо сведением к линейному ДУ заменой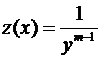 
;
· ДУ в полных дифференциалах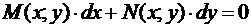 
при выполнении 
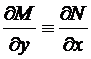, его общее решение 
, где функция 
находится из условий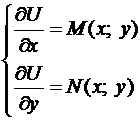 
;
· Уравнение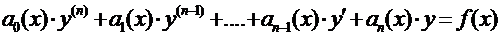 
при 
является Линейным Однородным ДУ (ЛОДУ), в противном случае ЛНДУ;
· Определитель Вронского для функций 
находится 
;
· Для n решений ЛОДУвыполнено:
1) Они линейно независимы 
;
2) Они линейно зависимы 
;
· Если дано ЛОДУ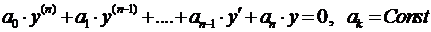 
, то характеристическое уравнение 
.
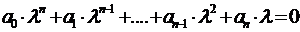· Если 
, то 
,
А)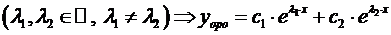 
;
Б)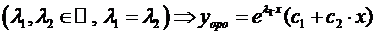 
;
В)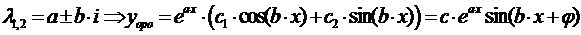 
,
, 
;
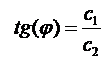· Если дано ЛНДУ 
то решение ищем в зависимости от корней характ-го ур-я
| Вид неоднородности | Вид решения 
|
| 
 − кратность корня 
|
| 
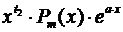
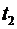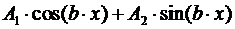
 − кратность корня 
|
| 
 − кратность корня 
|
| 
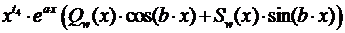 − кратность корня 
|
|  − кратность корня ,
|
|  ,
где  − решение при неодн-ти 
− решение при неодн-ти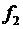 
|
− известный многочлен степени n и А - известное число,
− многочлен, для которого применяем метод неопределенных коэффициентов. Для этого предполагаемую функцию и её производные подставляем в исходное ДУ и приравниваем коэффициенты при соответствующих степенях правой и левой частей уравнения. Решение полученной системы и есть коэффициенты в решении;
· После нахождения 
записывают общее решение для ЛНДУ в виде 
. После этого учитывается начальное условие и выделяется частное решение при подстановке необходимых 
;
· Метод вариации постоянных: Для ЛНДУ ищем решение соответствующего ЛОДУ и находим фундаментальную систему решений (ФСР) 
. Тогда можно искать решение неоднородного уравнения в виде 
, где для производных неизвестных функций 
выполнено 
· Система дифференциальных уравнений 
с двумя искомыми функциями 
и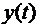 
имеет порядок 
(сумма старших порядков производных). В каноническом виде она записывается 
. К нормальному виду перейдём с увеличением числа искомых функций
, 
, 
;
· Решение системы ДУ методом исключения 
1) 
; 2)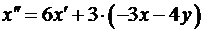 
, 
;
2) 
;
3) 
,
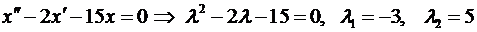общее решение 
;
4) 
,
;
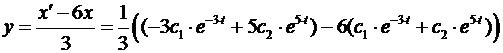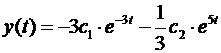5) Общее решение системы 
или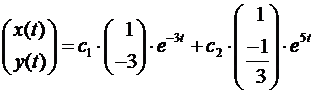 
т.е. собственные числа 
и 
, их собственные векторы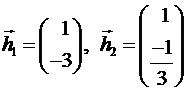 
и коллинеарные им векторы;
· Виды интегральных кривых (траекторий) и точки покоя для линейной однородной системы 2-го порядка с постоянными коэффициентами (в зависимости от собственных чисел) эффициентами внородной системы с постоянными аходим фундаментальную систему решений (ФСР)
1) 
действительные числа одного знака. Получаем искривленные параболы с общей вершиной, их ось задаёт один из собственных векторов (с наибольшим 
). Точка покоя ─ узел.
1.1) При 
точки удаляются от вершины с возрастанием
параметра t (времени), узел неустойчивый;
1.2) При 
точки приближаются к вершине с
возрастанием времени, узел устойчивый;
2) действительные числа разных знаков,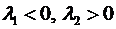 
. Получаем искривленные гиперболы с общим центром, для которых собственные векторы задают асимптоты. Их точки удаляются от центра и с возрастанием параметра t (времени)приближаются к оси, заданной вектором 
(с положительным 
). Точка покоя ─ седло;
3) 
чисто мнимые. Получаем множество искривленных эллипсов с общим центром в начале координат и осями по собственным векторам. Точка покоя ─ центр;
4) 
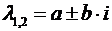комплексно-сопряженные. Получаем множество спиралей с бесконечным числом витков. Точка покоя ─ фокус.
4.1) Если 
, то при вращении вокруг центра точки
удаляются от него с возрастанием времени,
фокус неустойчивый;
4.2) Если 
, то при вращении вокруг центра точки
приближаются к нему с возрастанием времени,
фокус устойчивый;
5) При 
получаем множество прямых, параллельных между собой и собственному вектору 
.
5.1) При 
с возрастанием времени точки удаляются в обоих направлениях от прямой, заданной вектором ;
5.2)При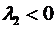 
с возрастанием времени точки приближаются в обоих направлениях к прямой, заданной вектором ;
Рекомендуемая литература
5.1 Основная литература:
1. 517(075)Ш 63
Шипачев, В. С. Высшая математика: учеб. пособие для бакалавров / В. С. Шипачев. - 8-е изд., перераб. и доп. - М.: Юрайт, 2012. - 447 с. - (Бакалавр, Базовый курс). - Рек. М-вом образования и науки РФ. - ISBN 978-5-9916-2031-4: 316-91.
Кол-во экземпляров: всего - 10
2. 517(075)Б 74
Богомолов Н. В. Математика: учеб.для бакалавров / Н. В. Богомолов, П. И. Самойленко. - 5-е изд., перераб. и доп. - М.: Юрайт, 2013. - 396 с. - (Бакалавр, Базовый курс). - Допущено М-вом образования и науки РФ.
- ISBN 978-5-9916-2568-5: 336-55.
Кол-во экземпляров: всего – 15
3. Фролов С.В. Высшая математика [ Электронный ресур с]: учеб. пособие/ Фролов С.В., Багаутдинова А.Ш.— [ Электрон. текстовые данные ]— СПб.: ГИОРД, 2012. — 616 c.— Режим доступа: ЭБС «IPRbooks», по паролю
4. Туганбаев А. А. Основы высшей математики: учеб.пособие для ВПО/А. А. Туганбаев. – 1-е изд. [ Электронный ресурс] — СПб.: Лань, 2011. — 491 с.
- Режим доступа «ЭБС ЛАНЬ»
5.2 дополнительная литература:
5. 517(075) Б 50
Бермант А. Ф. Краткий курс математического анализа: учеб.для вузов / А. Ф. Бермант, И. Г. Араманович. - 10-е изд., стер. - СПб.; М.; Краснодар: Лань, 2003. - 736 с. - (Учебники для вузов, Специальная литература). - Библиогр.: с. 736.
- ISBN 5-8114-0499-9: 280-00.
Кол-во экземпляров: всего – 30
6. 517(075) Д 17
Данко П. Е. Высшая математика в упражнениях и задачах: учеб.пособие для вузов: в 2 ч. Ч. 2 / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. - 6-е изд. - М.: Оникс 21 век: Мир и Образование, 2003. - 416 с.: ил. - С решениями. - ISBN 5-329-00528-0: 72-00. - ISBN 5-94666-009-8: 65-00. - ISBN 5-329-00327-X.
Кол-во экземпляров: всего – 52
7. 517 З-17
Зайцев И. А. Высшая математика: [учеб.пособие] / И. А. Зайцев. - 4-е изд., стер. - М.: Дрофа, 2005. - 398 с.: ил. - (Высшее образование). - Библиогр.: с. 392. - Рек. М-вом образования РФ для с.-х. вузов. - ISBN 5-7107-9071-0: 146-85.
Кол-во экземпляров: всего - 25
Методическое обеспечение
8. Золотарёв А.П. «Числовые и функциональные ряды». Учебно-методическое пособие по курсу «Математика». – Новоуральск, изд. НТИ, 2005. – 26 с.
5.4 Информационное обеспечение (включая перечень ресурсов информационно-телекоммуникационной сети «Интернет»)
1 http://nsti.ru
2 научная библиотека e-librari
3 ЭБС «Лань»
4 ЭБС «IPRbooks»
Орлов Ю.В. Учебно-методический комплекс (УМК)
дисциплины«Математика, 3 семестр». Учебно-методическое пособие для бакалавров заочной формы обучениянаправления 38.03.02 «Менеджмент».
– Новоуральск, изд. НТИ НИЯУ МИФИ, 2015. – 56 с.
