
Поиск:
Рекомендуем:
 Почему я выбрал профессую экономиста
Почему я выбрал профессую экономиста
 Почему одни успешнее, чем другие
Почему одни успешнее, чем другие
 Периферийные устройства ЭВМ
Периферийные устройства ЭВМ
 Нейроглия (или проще глия, глиальные клетки)
Нейроглия (или проще глия, глиальные клетки)
Категории:
Профессиональные компетенции
|
|
|
|

Поиск: Рекомендуем:  Почему я выбрал профессую экономиста
Почему я выбрал профессую экономиста
 Почему одни успешнее, чем другие
Почему одни успешнее, чем другие
 Периферийные устройства ЭВМ Периферийные устройства ЭВМ
 Нейроглия (или проще глия, глиальные клетки) Нейроглия (или проще глия, глиальные клетки)
Категории:
|
Профессиональные компетенции
| ||
| ПК-8 | владением навыками количественного и качественного анализа информации при принятии управленческих решений, построения экономических, финансовых и организационно-управленческих моделей путем их адаптации к конкретным задачам управления |
Контрольная работа

Вариант №1 (№1- 3б., №2 – 4 б., №3 – 7б., №4 – 6 б.)
№1 Для функции нескольких переменных 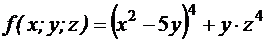 найти все частные производные первого порядка и вычислить их в точке М(1; 2; -1).
найти все частные производные первого порядка и вычислить их в точке М(1; 2; -1).
 №2 Для функции
№2 Для функции  изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
№3 Исследовать на локальные экстремумы функцию
 , найти её наибольшее и наименьшее значения в треугольнике АВС.
, найти её наибольшее и наименьшее значения в треугольнике АВС.
№4
Составить задачу линейного программирования о нахождении оптимального плана производства изделий К и М с наибольшей прибылью при ограничении по запасам сырья.
| Сырье | Расход на единицу | Запасы (кг) | |
| К | М | ||
| С1 | 2 | 2 | 200 |
| С2 | 2 | 8 | 320 |
| Прибыль (у.е.) с единицы | 4 | 3 | |
Графическим методом найти оптимальный план и максимальную прибыль. Составить двойственную задачу, решить её и проанализировать двойственные оценки сырья.
Вариант №2 (№1- 3б., №2 – 4 б., №3 – 7б., №4 – 6 б.)
№1 Для функции нескольких переменных  найти все частные производные первого порядка и вычислить их в точке М(1; 2; 1).
найти все частные производные первого порядка и вычислить их в точке М(1; 2; 1).
 №2 Для функции
№2 Для функции  изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
№3 Исследовать на локальные экстремумы функцию
 , найти её наибольшее и наименьшее значения в треугольнике АВС.
, найти её наибольшее и наименьшее значения в треугольнике АВС.
№4
Составить задачу линейного программирования о нахождении оптимального плана производства изделий К и М с наибольшей прибылью при ограничении по запасам сырья.
| Сырье | Расход на единицу | Запасы (кг) | |
| К | М | ||
| С1 | 2 | 2 | 400 |
| С2 | 4 | 1 | 160 |
| Прибыль (у.е.) с единицы | 10 | 12 | |
Графическим методом найти оптимальный план и максимальную прибыль. Составить двойственную задачу, решить её и проанализировать двойственные оценки сырья.
Вариант №3 (№1- 3б., №2 – 4 б., №3 – 7б., №4 – 6 б.)
№1 Для функции нескольких переменных  найти все частные производные первого порядка и вычислить их в точке М(0; 2; 1).
найти все частные производные первого порядка и вычислить их в точке М(0; 2; 1).
 №2 Для функции
№2 Для функции  изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
№3 Исследовать на локальные экстремумы функцию
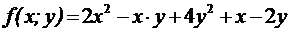 , найти её наибольшее и наименьшее значения в треугольнике АВС.
, найти её наибольшее и наименьшее значения в треугольнике АВС.
№4
Составить задачу линейного программирования о нахождении оптимального плана производства изделий К и М с наибольшей прибылью при ограничении по запасам сырья.
| Сырье | Расход на единицу | Запасы (кг) | |
| К | М | ||
| С1 | 2 | 2 | 400 |
| С2 | 4 | 1 | 160 |
| Прибыль (у.е.) с единицы | 10 | 12 | |
Графическим методом найти оптимальный план и максимальную прибыль. Составить двойственную задачу, решить её и проанализировать двойственные оценки сырья.
Вариант №4 (№1- 3б., №2 – 4 б., №3 – 7б., №4 – 6 б.)
№1 Для функции нескольких переменных  найти все частные производные первого порядка и вычислить их в точке М(1; 2; -1).
найти все частные производные первого порядка и вычислить их в точке М(1; 2; -1).
 №2 Для функции
№2 Для функции  изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
№3 Исследовать на локальные экстремумы функцию
 , найти её наибольшее и наименьшее значения в треугольнике АВС.
, найти её наибольшее и наименьшее значения в треугольнике АВС.
№4
Составить задачу линейного программирования о нахождении оптимального плана производства изделий К и М с наибольшей прибылью при ограничении по запасам сырья.
| Сырье | Расход на единицу | Запасы (кг) | |
| К | М | ||
| С1 | 5 | 1 | 600 |
| С2 | 2 | 2 | 400 |
| Прибыль (у.е.) с единицы | 10 | 20 | |
Графическим методом найти оптимальный план и максимальную прибыль. Составить двойственную задачу, решить её и проанализировать двойственные оценки сырья.
Вариант №5 (№1- 3б., №2 – 4 б., №3 – 7б., №4 – 6 б.)
№1 Для функции нескольких переменных  найти все частные производные первого порядка и вычислить их в точке М(1; 2; -1).
найти все частные производные первого порядка и вычислить их в точке М(1; 2; -1).
 №2 Для функции
№2 Для функции  изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
№3 Исследовать на локальные экстремумы функцию
 , найти её наибольшее и наименьшее значения в треугольнике АВС.
, найти её наибольшее и наименьшее значения в треугольнике АВС.
№4
Составить задачу линейного программирования о нахождении оптимального плана производства изделий К и М с наибольшей прибылью при ограничении по запасам сырья.
| Сырье | Расход на единицу | Запасы (кг) | |
| К | М | ||
| С1 | 1 | 4 | 160 |
| С2 | 2 | 2 | 200 |
| Прибыль (у.е.) с единицы | 4 | 3 | |
Графическим методом найти оптимальный план и максимальную прибыль. Составить двойственную задачу, решить её и проанализировать двойственные оценки сырья.
Вариант №6 (№1- 3б., №2 – 4 б., №3 – 7б., №4 – 6 б.)
№1 Для функции нескольких переменных  найти все частные производные первого порядка и вычислить их в точке М(1; 1; -1).
найти все частные производные первого порядка и вычислить их в точке М(1; 1; -1).
 №2 Для функции
№2 Для функции  изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
№3 Исследовать на локальные экстремумы функцию
 , найти её наибольшее и наименьшее значения в треугольнике АВС.
, найти её наибольшее и наименьшее значения в треугольнике АВС.
№4
Составить задачу линейного программирования о нахождении оптимального плана производства изделий К и М с наибольшей прибылью при ограничении по запасам сырья.
| Сырье | Расход на единицу | Запасы (кг) | |
| К | М | ||
| С1 | 4 | 4 | 800 |
| С2 | 5 | 1 | 600 |
| Прибыль (у.е.) с единицы | 30 | 20 | |
Графическим методом найти оптимальный план и максимальную прибыль. Составить двойственную задачу, решить её и проанализировать двойственные оценки сырья.
Вариант №7 (№1- 3б., №2 – 4 б., №3 – 7б., №4 – 6 б.)
№1 Для функции нескольких переменных  найти все частные производные первого порядка и вычислить их в точке М(2; 1; -1).
найти все частные производные первого порядка и вычислить их в точке М(2; 1; -1).
 №2 Для функции
№2 Для функции  изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
№3 Исследовать на локальные экстремумы функцию
 , найти её наибольшее и наименьшее значения в треугольнике АВС.
, найти её наибольшее и наименьшее значения в треугольнике АВС.
№4
Составить задачу линейного программирования о нахождении оптимального плана производства изделий К и М с наибольшей прибылью при ограничении по запасам сырья.
| Сырье | Расход на единицу | Запасы (кг) | |
| К | М | ||
| С1 | 1 | 5 | 600 |
| С2 | 5 | 1 | 600 |
| Прибыль (у.е.) с единицы | 14 | 20 | |
Графическим методом найти оптимальный план и максимальную прибыль. Составить двойственную задачу, решить её и проанализировать двойственные оценки сырья.
Вариант №8 (№1- 3б., №2 – 4 б., №3 – 7б., №4 – 6 б.)
№1 Для функции нескольких переменных  найти все частные производные первого порядка и вычислить их в точке М(2; 1; -1).
найти все частные производные первого порядка и вычислить их в точке М(2; 1; -1).
 №2 Для функции
№2 Для функции  изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
№3 Исследовать на локальные экстремумы функцию
 , найти её наибольшее и наименьшее значения в треугольнике АВС.
, найти её наибольшее и наименьшее значения в треугольнике АВС.
№4
Составить задачу линейного программирования о нахождении оптимального плана производства изделий К и М с наибольшей прибылью при ограничении по запасам сырья.
| Сырье | Расход на единицу | Запасы (кг) | |
| К | М | ||
| С1 | 4 | 4 | 800 |
| С2 | 5 | 1 | 600 |
| Прибыль (у.е.) с единицы | 20 | 20 | |
Графическим методом найти оптимальный план и максимальную прибыль. Составить двойственную задачу, решить её и проанализировать двойственные оценки сырья.
Вариант №9 (№1- 3б., №2 – 4 б., №3 – 7б., №4 – 6 б.)
№1 Для функции нескольких переменных  найти все частные производные первого порядка и вычислить их в точке М(1; 2; -1).
найти все частные производные первого порядка и вычислить их в точке М(1; 2; -1).
 №2 Для функции
№2 Для функции  изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
№3 Исследовать на локальные экстремумы функцию
 , найти её наибольшее и наименьшее значения в треугольнике АВС.
, найти её наибольшее и наименьшее значения в треугольнике АВС.
№4
Составить задачу линейного программирования о нахождении оптимального плана производства изделий К и М с наибольшей прибылью при ограничении по запасам сырья.
| Сырье | Расход на единицу | Запасы (кг) | |
| К | М | ||
| С1 | 10 | 90 | 900 |
| С2 | 9 | 2 | 198 |
| Прибыль (у.е.) с единицы | 10 | 20 | |
Графическим методом найти оптимальный план и максимальную прибыль. Составить двойственную задачу, решить её и проанализировать двойственные оценки сырья.
Вариант №10 (№1- 3б., №2 – 4 б., №3 – 7б., №4 – 6 б.)
№1 Для функции нескольких переменных  найти все частные производные первого порядка и вычислить их в точке М(2; 1; -1).
найти все частные производные первого порядка и вычислить их в точке М(2; 1; -1).
 №2 Для функции
№2 Для функции  изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
№3 Исследовать на локальные экстремумы функцию
 , найти её наибольшее и наименьшее значения в треугольнике АВС.
, найти её наибольшее и наименьшее значения в треугольнике АВС.
№4
Составить задачу линейного программирования о нахождении оптимального плана производства изделий К и М с наибольшей прибылью при ограничении по запасам сырья.
| Сырье | Расход на единицу | Запасы (кг) | |
| К | М | ||
| С1 | 2 | 2 | 400 |
| С2 | 10 | 2 | 1200 |
| Прибыль (у.е.) с единицы | 20 | 20 | |
Графическим методом найти оптимальный план и максимальную прибыль. Составить двойственную задачу, решить её и проанализировать двойственные оценки сырья.
Вариант №11 (№1- 3б., №2 – 4 б., №3 – 7б., №4 – 6 б.)
№1 Для функции нескольких переменных  найти все частные производные первого порядка и вычислить их в точке М(1; 2; -1).
найти все частные производные первого порядка и вычислить их в точке М(1; 2; -1).
 №2 Для функции
№2 Для функции  изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
№3 Исследовать на локальные экстремумы функцию
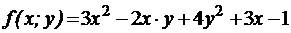 , найти её наибольшее и наименьшее значения в треугольнике АВС.
, найти её наибольшее и наименьшее значения в треугольнике АВС.
№4
Составить задачу линейного программирования о нахождении оптимального плана производства изделий К и М с наибольшей прибылью при ограничении по запасам сырья.
| Сырье | Расход на единицу | Запасы (кг) | |
| К | М | ||
| С1 | 3 | 3 | 300 |
| С2 | 2 | 2 | 180 |
| Прибыль (у.е.) с единицы | 10 | 20 | |
Графическим методом найти оптимальный план и максимальную прибыль. Составить двойственную задачу, решить её и проанализировать двойственные оценки сырья.
Вариант №12 (№1- 3б., №2 – 4 б., №3 – 7б., №4 – 6 б.)
№1 Для функции нескольких переменных  найти все частные производные первого порядка и вычислить их в точке М(1; 1; -1).
найти все частные производные первого порядка и вычислить их в точке М(1; 1; -1).
 №2 Для функции
№2 Для функции  изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
№3 Исследовать на локальные экстремумы функцию
 , найти её наибольшее и наименьшее значения в треугольнике АВС.
, найти её наибольшее и наименьшее значения в треугольнике АВС.
№4
Составить задачу линейного программирования о нахождении оптимального плана производства изделий К и М с наибольшей прибылью при ограничении по запасам сырья.
| Сырье | Расход на единицу | Запасы (кг) | |
| К | М | ||
| С1 | 5 | 1 | 600 |
| С2 | 1 | 1 | 200 |
| Прибыль (у.е.) с единицы | 10 | 15 | |
Графическим методом найти оптимальный план и максимальную прибыль. Составить двойственную задачу, решить её и проанализировать двойственные оценки сырья.
Вариант №13 (№1- 3б., №2 – 4 б., №3 – 7б., №4 – 6 б.)
№1 Для функции нескольких переменных 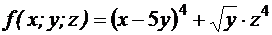 найти все частные производные первого порядка и вычислить их в точке М(1; 1; -1).
найти все частные производные первого порядка и вычислить их в точке М(1; 1; -1).
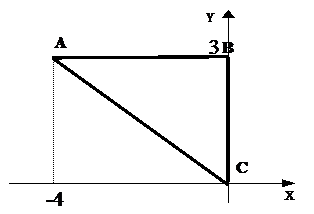 №2 Для функции
№2 Для функции  изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
№3 Исследовать на локальные экстремумы функцию
 , найти её наибольшее и наименьшее значения в треугольнике АВС.
, найти её наибольшее и наименьшее значения в треугольнике АВС.
№4
Составить задачу линейного программирования о нахождении оптимального плана производства изделий К и М с наибольшей прибылью при ограничении по запасам сырья.
| Сырье | Расход на единицу | Запасы (кг) | |
| К | М | ||
| С1 | 6 | 6 | 600 |
| С2 | 2 | 8 | 320 |
| Прибыль (у.е.) с единицы | 2 | 5 | |
Графическим методом найти оптимальный план и максимальную прибыль. Составить двойственную задачу, решить её и проанализировать двойственные оценки сырья.
Вариант №14 (№1- 3б., №2 – 4 б., №3 – 7б., №4 – 6 б.)
№1 Для функции нескольких переменных  найти все частные производные первого порядка и вычислить их в точке М(1; 1; -1).
найти все частные производные первого порядка и вычислить их в точке М(1; 1; -1).
 №2 Для функции
№2 Для функции  изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
№3 Исследовать на локальные экстремумы функцию
 , найти её наибольшее и наименьшее значения в треугольнике АВС.
, найти её наибольшее и наименьшее значения в треугольнике АВС.
№4
Составить задачу линейного программирования о нахождении оптимального плана производства изделий К и М с наибольшей прибылью при ограничении по запасам сырья.
| Сырье | Расход на единицу | Запасы (кг) | |
| К | М | ||
| С1 | 5 | 1 | 600 |
| С2 | 1 | 1 | 200 |
| Прибыль (у.е.) с единицы | 10 | 15 | |
Графическим методом найти оптимальный план и максимальную прибыль. Составить двойственную задачу, решить её и проанализировать двойственные оценки сырья.
Вариант №15 (№1- 3б., №2 – 4 б., №3 – 7б., №4 – 6 б.)
№1 Для функции нескольких переменных 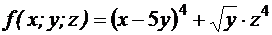 найти все частные производные первого порядка и вычислить их в точке М(1; 1; -1).
найти все частные производные первого порядка и вычислить их в точке М(1; 1; -1).
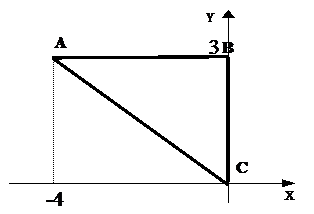 №2 Для функции
№2 Для функции  изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
№3 Исследовать на локальные экстремумы функцию
 , найти её наибольшее и наименьшее значения в треугольнике АВС.
, найти её наибольшее и наименьшее значения в треугольнике АВС.
№4
Составить задачу линейного программирования о нахождении оптимального плана производства изделий К и М с наибольшей прибылью при ограничении по запасам сырья.
| Сырье | Расход на единицу | Запасы (кг) | |
| К | М | ||
| С1 | 6 | 6 | 600 |
| С2 | 2 | 8 | 320 |
| Прибыль (у.е.) с единицы | 2 | 5 | |
Графическим методом найти оптимальный план и максимальную прибыль. Составить двойственную задачу, решить её и проанализировать двойственные оценки сырья.
Вариант №16 (№1- 3б., №2 – 4 б., №3 – 7б., №4 – 6 б.)
№1 Для функции нескольких переменных  найти все частные производные первого порядка и вычислить их в точке М(1; 1; -1).
найти все частные производные первого порядка и вычислить их в точке М(1; 1; -1).
 №2 Для функции
№2 Для функции  изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
изобразить линии уровня, в точках А(1; 2), В(-1; 3), С(-2; -2) изобразить направления её наибольшего возрастания. В точке А найти значение производной по направлению к точке В.
№3 Исследовать на локальные экстремумы функцию
 , найти её наибольшее и наименьшее значения в треугольнике АВС.
, найти её наибольшее и наименьшее значения в треугольнике АВС.
№4
Составить задачу линейного программирования о нахождении оптимального плана производства изделий К и М с наибольшей прибылью при ограничении по запасам сырья.
| Сырье | Расход на единицу | Запасы (кг) | |
| К | М | ||
| С1 | 5 | 1 | 600 |
| С2 | 1 | 1 | 200 |
| Прибыль (у.е.) с единицы | 10 | 15 | |
Графическим методом найти оптимальный план и максимальную прибыль. Составить двойственную задачу, решить её и проанализировать двойственные оценки сырья.

Вариант №1
№1 Для каждого дифференциального уравнения
а) Определить его вид;
б) Найти общее решение (общий интеграл);
в) При указанных начальных условиях решить задачу Коши
1)  , у (1)=2;
, у (1)=2;
2)  , p =1 при s =1;
, p =1 при s =1;
3)  .
.
№2 Найти решение линейных уравнений

№3 Найти общее и частное решения дифференциального уравнения
 ;
;
№4 Дана система линейных дифференциальных уравнений

Методом исключения общее решение системы, записать его в векторном виде; Указать собственные числа и собственные векторы; Изобразить интегральные кривые такой в окрестности точки покоя и исследовать её на устойчивость; Найти частное решение системы при указанных начальных условиях;
Вариант №2
№1 Для каждого дифференциального уравнения
а) Определить его вид;
б) Найти общее решение (общий интеграл);
в) При указанных начальных условиях решить задачу Коши
1)  , у (1)= -1;
, у (1)= -1;
2)  , t =1 при s =1;
, t =1 при s =1;
3) 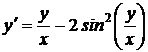 .
.
№2 Найти решение линейных уравнений
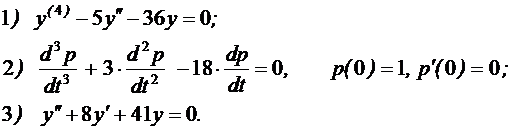
№3 Найти общее и частное решения дифференциального уравнения
 ;
;
№4 Дана система линейных дифференциальных уравнений

Методом исключения общее решение системы, записать его в векторном виде; Указать собственные числа и собственные векторы; Изобразить интегральные кривые такой в окрестности точки покоя и исследовать её на устойчивость; Найти частное решение системы при указанных начальных условиях;
Вариант №3
№1 Для каждого дифференциального уравнения
а) Определить его вид;
б) Найти общее решение (общий интеграл);
в) При указанных начальных условиях решить задачу Коши
1)  ;
;
2) 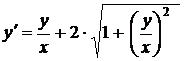 , у =1 при х =1;
, у =1 при х =1;
3)  , p =1 при t =
, p =1 при t = 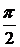 .
.
№2 Найти решение линейных уравнений

№3 Найти общее и частное решения дифференциального уравнения
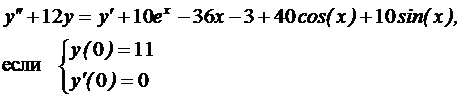 ;
;
№4 Дана система линейных дифференциальных уравнений

Методом исключения общее решение системы, записать его в векторном виде; Указать собственные числа и собственные векторы; Изобразить интегральные кривые такой в окрестности точки покоя и исследовать её на устойчивость; Найти частное решение системы при указанных начальных условиях;
Вариант №4
№1 Для каждого дифференциального уравнения
а) Определить его вид;
б) Найти общее решение (общий интеграл);
в) При указанных начальных условиях решить задачу Коши
1)  , у (0)=2;
, у (0)=2;
2)  , h =1 при t =1;
, h =1 при t =1;
3)  .
.
№2 Найти решение линейных уравнений
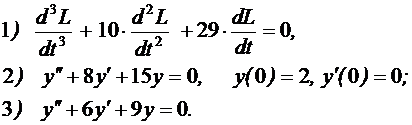
№3 Найти общее и частное решения дифференциального уравнения
 ;
;
№4 Дана система линейных дифференциальных уравнений

Методом исключения общее решение системы, записать его в векторном виде; Указать собственные числа и собственные векторы; Изобразить интегральные кривые такой в окрестности точки покоя и исследовать её на устойчивость; Найти частное решение системы при указанных начальных условиях;
Вариант №5
№1 Для каждого дифференциального уравнения
а) Определить его вид;
б) Найти общее решение (общий интеграл);
в) При указанных начальных условиях решить задачу Коши
1)  , у =0 при х =1;
, у =0 при х =1;
2)  ;
;
3) 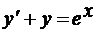 , у (1)= e.
, у (1)= e.
№2 Найти решение линейных уравнений

№3 Найти общее и частное решения дифференциального уравнения
 ;
;
№4 Дана система линейных дифференциальных уравнений

Методом исключения общее решение системы, записать его в векторном виде; Указать собственные числа и собственные векторы; Изобразить интегральные кривые такой в окрестности точки покоя и исследовать её на устойчивость; Найти частное решение системы при указанных начальных условиях;
Вариант №6
№1 Для каждого дифференциального уравнения
а) Определить его вид;
б) Найти общее решение (общий интеграл);
в) При указанных начальных условиях решить задачу Коши
1)  , y (1)=2;
, y (1)=2;
2)  ;
;
3)  , y =0 при х =0.
, y =0 при х =0.
№2 Найти решение линейных уравнений
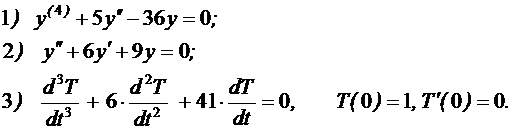
№3 Найти общее и частное решения дифференциального уравнения
 ;
;
№4 Дана система линейных дифференциальных уравнений

Методом исключения общее решение системы, записать его в векторном виде; Указать собственные числа и собственные векторы; Изобразить интегральные кривые такой в окрестности точки покоя и исследовать её на устойчивость; Найти частное решение системы при указанных начальных условиях;
Вариант №7
№1 Для каждого дифференциального уравнения
а) Определить его вид;
б) Найти общее решение (общий интеграл);
в) При указанных начальных условиях решить задачу Коши
1)  ;
;
2)  , у(1)=2;
, у(1)=2;
3)  , p =3 t =0.
, p =3 t =0.
№2 Найти решение линейных уравнений

№3 Найти общее и частное решения дифференциального уравнения
 ;
;
№4 Дана система линейных дифференциальных уравнений

Методом исключения общее решение системы, записать его в векторном виде; Указать собственные числа и собственные векторы; Изобразить интегральные кривые такой в окрестности точки покоя и исследовать её на устойчивость; Найти частное решение системы при указанных начальных условиях;
Вариант №8
№1 Для каждого дифференциального уравнения
а) Определить его вид;
б) Найти общее решение (общий интеграл);
в) При указанных начальных условиях решить задачу Коши
1)  ,
,  ;
;
2)  ;
;
3)  , y (0)=2.
, y (0)=2.
№2 Найти решение линейных уравнений

№3 Найти общее и частное решения дифференциального уравнения
 ;
;
№4 Дана система линейных дифференциальных уравнений

Методом исключения общее решение системы, записать его в векторном виде; Указать собственные числа и собственные векторы; Изобразить интегральные кривые такой в окрестности точки покоя и исследовать её на устойчивость; Найти частное решение системы при указанных начальных условиях;
Вариант №9
№1 Для каждого дифференциального уравнения
а) Определить его вид;
б) Найти общее решение (общий интеграл);
в) При указанных начальных условиях решить задачу Коши
1)  ;
;
2)  , y =2 x =1;
, y =2 x =1;
3)  , y (1)= e + 1.
, y (1)= e + 1.
№2 Найти решение линейных уравнений
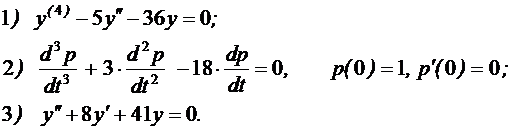
№3 Найти общее и частное решения дифференциального уравнения
 ;
;
№4 Дана система линейных дифференциальных уравнений

Методом исключения общее решение системы, записать его в векторном виде; Указать собственные числа и собственные векторы; Изобразить интегральные кривые такой в окрестности точки покоя и исследовать её на устойчивость; Найти частное решение системы при указанных начальных условиях;
Вариант №10
№1 Для каждого дифференциального уравнения
а) Определить его вид;
б) Найти общее решение (общий интеграл);
в) При указанных начальных условиях решить задачу Коши
1)  ,
,  ;
;
2)  , y (1)= -2;
, y (1)= -2;
3) 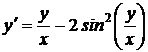 .
.
№2 Найти решение линейных уравнений

№3 Найти общее и частное решения дифференциального уравнения
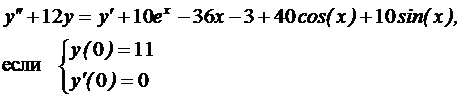 ;
;
№4 Дана система линейных дифференциальных уравнений

Методом исключения общее решение системы, записать его в векторном виде; Указать собственные числа и собственные векторы; Изобразить интегральные кривые такой в окрестности точки покоя и исследовать её на устойчивость; Найти частное решение системы при указанных начальных условиях;
Вариант №11
№1 Для каждого дифференциального уравнения
а) Определить его вид;
б) Найти общее решение (общий интеграл);
в) При указанных начальных условиях решить задачу Коши
1)  ;
;
2) 
3)  .
.
№2 Найти решение линейных уравнений
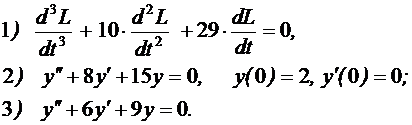
№3 Найти общее и частное решения дифференциального уравнения
 ;
;
№4 Дана система линейных дифференциальных уравнений

Методом исключения общее решение системы, записать его в векторном виде; Указать собственные числа и собственные векторы; Изобразить интегральные кривые такой в окрестности точки покоя и исследовать её на устойчивость; Найти частное решение системы при указанных начальных условиях;
Вариант №12
№1 Для каждого дифференциального уравнения
а) Определить его вид;
б) Найти общее решение (общий интеграл);
в) При указанных начальных условиях решить задачу Коши
1)  ;
;
2)  ;
;
3)  ;
;
№2 Найти решение линейных уравнений

№3 Найти общее и частное решения дифференциального уравнения
 ;
;
№4 Дана система линейных дифференциальных уравнений

Методом исключения общее решение системы, записать его в векторном виде; Указать собственные числа и собственные векторы; Изобразить интегральные кривые такой в окрестности точки покоя и исследовать её на устойчивость; Найти частное решение системы при указанных начальных условиях;
Вариант №13
№1 Для каждого дифференциального уравнения
а) Определить его вид;
б) Найти общее решение (общий интеграл);
в) При указанных начальных условиях решить задачу Коши
1)  ;
;
2)  ;
;
3)  .
.
№2 Найти решение линейных уравнений
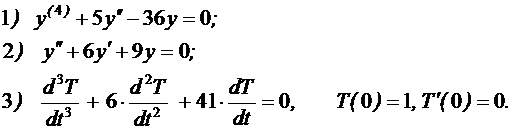
№3 Найти общее и частное решения дифференциального уравнения
 ;
;
№4 Дана система линейных дифференциальных уравнений

Методом исключения общее решение системы, записать его в векторном виде; Указать собственные числа и собственные векторы; Изобразить интегральные кривые такой в окрестности точки покоя и исследовать её на устойчивость; Найти частное решение системы при указанных начальных условиях;
Вариант №14
№1 Для каждого дифференциального уравнения
а) Определить его вид;
б) Найти общее решение (общий интеграл);
в) При указанных начальных условиях решить задачу Коши
1)  ;
;
2)  ;
;
3)  .
.
№2 Найти решение линейных уравнений

№3 Найти общее и частное решения дифференциального уравнения
 ;
;
№4 Дана система линейных дифференциальных уравнений

Методом исключения общее решение системы, записать его в векторном виде; Указать собственные числа и собственные векторы; Изобразить интегральные кривые такой в окрестности точки покоя и исследовать её на устойчивость; Найти частное решение системы при указанных начальных условиях;
Вариант №15
№1 Для каждого дифференциального уравнения
а) Определить его вид;
б) Найти общее решение (общий интеграл);
в) При указанных начальных условиях решить задачу Коши
1)  ;
;
2) 
3) 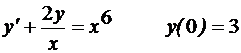 .
.
№2 Найти решение линейных уравнений

№3 Найти общее и частное решения дифференциального уравнения
 ;
;
№4 Дана система линейных дифференциальных уравнений

Методом исключения общее решение системы, записать его в векторном виде; Указать собственные числа и собственные векторы; Изобразить интегральные кривые такой в окрестности точки покоя и исследовать её на устойчивость; Найти частное решение системы при указанных начальных условиях;
Вариант №16
№1 Для каждого дифференциального уравнения
а) Определить его вид;
б) Найти общее решение (общий интеграл);
в) При указанных начальных условиях решить задачу Коши
1)  , y (1)=-1;
, y (1)=-1;
2)  , y =1 при x =2;
, y =1 при x =2;
3)  .
.
№2 Найти решение линейных уравнений
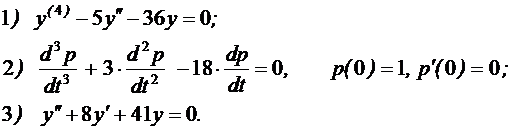
№3 Найти общее и частное решения дифференциального уравнения
 ;
;
№4 Дана система линейных дифференциальных уравнений

Методом исключения общее решение системы, записать его в векторном виде; Указать собственные числа и собственные векторы; Изобразить интегральные кривые такой в окрестности точки покоя и исследовать её на устойчивость; Найти частное решение системы при указанных начальных условиях;
|
|
|
|
|
|
Дата добавления: 2018-10-14; Мы поможем в написании ваших работ!; просмотров: 355 | Нарушение авторских прав
Лучшие изречения: