В ОТКРЫТЫХ ПРИЗМАТИЧЕСКИХ РУСЛАХ
Существует много способов расчета кривых свободной поверхности. Их можно разделить на две группы в зависимости от подхода к принятию 
и соответствующих им значений 
. Согласно первому подходу задаются постоянным значением 
и вычисляют по (17.10) , согласно второму задаются значениями ,a вычисляют по (17.10), причем могут получиться и не целые числа.
Способ И. И. Агроскина. Значение задано, 
; a=ah/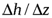 
.
Тогда по (17.10)
.
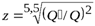Учитывая, что
;
получаем
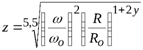. (17.21)
Далее по (17.8)
.
Индекс нуль, как и ранее, соответствует равномерному движению. Для различных форм живого сечения выражения для и 
имеют различный вид.
Трапецеидальное поперечное сечение. Как известно из (16.24), 
. Тогда
,
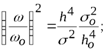
где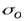 
-характеристика живого сечения при равномерном движении, т. е. при 
и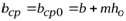 
.
Подставив полученные выражения для 
и 
в (17.21), найдем
Если учесть, что 
может быть принят приблизительно равным 0,2, то 
. Тогда становится ясным, почему принят 
.
Обозначим
(17.22)
тогда
. (17.23)
В каждой задаче выражения 
- постоянная величина.
Параметр по (17.8) с учетом 
, и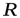 
, выраженных через ширину трапеции по дну 
,
, (17.24)
где 
- коэффициент шероховатости.
Здесь обозначено
. (17.25)
Значения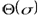 
, вычисленные по (17.25) при 
затабулированы.
Выражение 
в каждой задаче - постоянная величина.
Параболическое поперечное сечение. В этом случае 
и 
. Тогда из (17.21) при этом же =5,5 (что даст возможность использовать те же значения при =5,5, что и для трапеций), если обозначить
, (17.26)
Получим
.
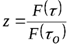Параметр 
для параболического русла найдется вновь по (17.8) с учетом соотношений между элементами такого русла:
. (17.27)
Соответственно 
. В каждой задаче 
и 
- постоянные величины.
Обращает на себя внимание однотипность выражений для и при расчетах по Агроскину в руслах с различной формой поперечного сечения. Величина равна частному от деления функции 
, 
на постоянное в каждой задаче значение той же функции, но при равномерном движении, т. е. 
, 
. Параметр кинетичности равен произведению 
на линейный параметр в степени 
, т. е. 
, и на функцию 
характеристики живого сечения, т. е. ,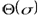 
. Наличие таблиц существенно облегчает выполнение расчетов. Изменение в пределах 
незначительно сказывается на длине рассчитываемых кривых свободной поверхности.
В заключение укажем, что, принимая другие целые значения , не равные единице, например 2; 3; 4, получим при 
при 
; при 
и т.д. И тогда можно непосредственно выполнить интегрирование, т. е., не применяя таблиц, найти необходимые значения функций 
или 
или 
. Определив в каждом случае, найдем длину кривой свободной поверхности.
Длина кривой свободной поверхности независимо от выбранного значения получится практически одной и той же. Связано это с тем, что при разных значения , как было показано, будут различными. Различными будут и значения, и значения функций 
при 
, при 
и при 
, которые определяются в зависимости от принятого значения 
.
Способ Б. А. Бахметева. Б. А Бахметевым было установлено, что для многих форм поперечного сечения русл (для которых расходная характеристика 
является монотонно возрастающей функцией глубины 
) существует показательная зависимость
, (7.28)
где 
и 
- две произвольно взятые глубины в данном поперечном сечении русла; 
и 
- соответствующие им расходные характеристики.
Эта зависимость - приближенная и строгого теоретического обоснования не получила, но она находит довольно широкое применение и дает вполне удовлетворительные результаты. Величина называется гидравлическим показателем русла. Приближенно считается, что гидравлический показатель русла постоянен для данного поперечного сечения русла и не зависит от глубины. Однако это справедливо лишь для некоторых русл. К ним относятся узкие прямоугольные русла (), широкие (
) прямоугольные (
) и некоторые другие.
Для прямоугольных, трапецеидальных и параболических русл (кроме широких и узких) при показатель определяется по вытекающему из (17.28) выражению
,
где 
- средняя глубина на рассчитываемом участке; 
- расходная характеристика при этой глубине.
Так как для указанных русл показатель зависит от глубины, то выбор именно таких величин (
и 
, и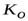 
) дает необходимую точность при расчетах.
Для русл с замкнутым и составным поперечным сечением зависимость (17.28) вообще неприменима.
При расчетах по способу Б. А. Бахметева длина кривых свободной поверхности определяется по (17.15), (17 17) и (17.19) при уклонах дна 
и соответственно.
По Б. А. Бахметеву при , приняв в (17.28) глубины 
и 
, имеем 
, 
или 
. Далее
.
Длина кривой свободной поверхности определяется по (17.15), функция 
- по (17.16); 
; 
.
При 
и длина кривой свободной поверхности определяется по (17.17), а функция - по (17.18), 
- фиктивная нормальная глубина при равномерном движении с расходом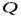 
в русле с уклоном 
.
При длина 
определяется по (17.19), по (17.20), в качестве произвольного положительного уклона здесь принят 
,a 
; 
.
Гидравлический показатель русла определяется при 
(17.29); при
,
где 
; при
,
где 
.
Последовательность расчета кривых свободной поверхности в открытых призматических руслах. При расчете кривых свободной поверхности чаще всего необходимо найти значения глубин в различных створах, разбивающих рассчитываемую кривую на участки, и, суммируя длины отдельных участков, найти длину кривой свободной поверхности, т. е. построить кривую.
При расчете сначала определяются нормальная глубина и критическая глубина (если необходимо, то и критический уклон ). Затем в результате анализа устанавливается тип кривой свободной поверхности, асимптоты этой кривой, определяются граничные глубины. При этом могут быть известны обе граничные глубины из гидравлического расчета сооружения (например, верхняя и нижняя глубины для кривой подпора 
). В других случаях из гидравлического расчета сооружения известна лишь одна глубина, а вторая назначается так, чтобы она, например, отличалась от нормальной глубины на 1-3 % (рис. 17.2, 17.3, 17.7).
После определения граничных глубин весь участок кривой свободной поверхности разбивается на ряд расчетных участков. Последовательно переходя от одного участка к другому, вычисляя глубину на одной границе участка при известной глубине на другой границе участка и длину участка кривой свободной поверхности, можно выполнить расчет всей кривой подпора или спада.
