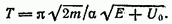Речной поток
Изучение речного потока и его свойств необходимо судоводителю для правильного определения направления и скорости течения, горизонтов и уклонов потока, внутренних течений в потоке, действия их на судно и т. д.
Если мысленно разрезать реку поперек течения вертикальной плоскостью, перпендикулярной к плоскости поверхности воды, то площадь сечения, ограниченная дном, берегом и поверхностью воды, называется живым сечением. Количество воды, проходящее через живое сечение в течение одной секунды, называется расходом воды. Скорость течения зависит от глубины и формы русла и распределяется по живому сечению неравномерно. Так, например, характер течения на прямых участках отличается от течения в закруглениях, а течение на перекатах — от течения на плесе и т. д.
В разных местах живого сечения скорость течения различна (рис. 9). В любом живом сечении максимальная скорость течения находится над самым глубоким местом около поверхности воды или несколько ниже ее, примерно до одной трети глубины от поверхности воды. От точки живого сечения, отстоящей на одну треть от поверхности воды, скорость течения уменьшается ко дну реки и от середины реки к берегам.
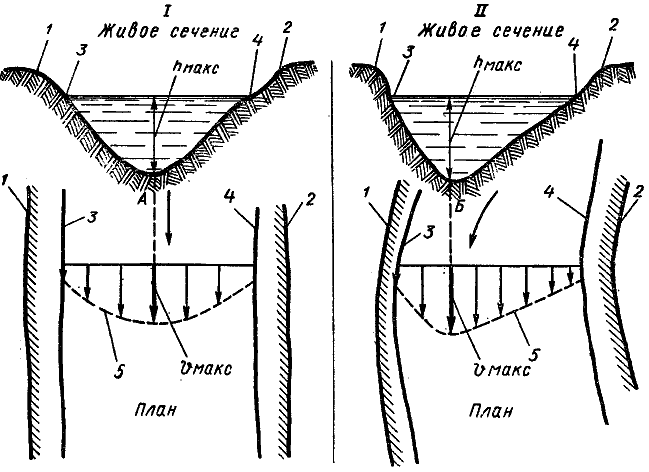 Рис. 9. Распределение поверхностных скоростей течения в плане: / — симметричное русло; 11 — несимметричное русло. 1 — бровка правого берега; 2 — бровка левого берега; 3 — правый урез воды; 4 — левый урез воды; 5 — распределение скоростей течения в плане
Рис. 9. Распределение поверхностных скоростей течения в плане: / — симметричное русло; 11 — несимметричное русло. 1 — бровка правого берега; 2 — бровка левого берега; 3 — правый урез воды; 4 — левый урез воды; 5 — распределение скоростей течения в плане
Таким образом, наибольшая скорость течения в прямых; русла находится в середине симметричного русла, а в криволинейных участках — ближе к вогнутому берегу.
Если на отрезке реки, состоящем из криволинейных и прямых участков, мысленно сделать некоторое количество живых сечений, а точки максимальных скоростей течения каждого живого сечения соединить линией, то получим ось динамического потока —стрежень, который близко подходит к вогнутости берегов (если они вогнуты) и идет посередине в прямых участках.
Умение распознать направление и линию стрежня очень важно для судоводителя любого судна.
3. Внутренние течения в потоке
В живом сечении изгибов русла под действием центробежной силы внутреннее течение направлено по наклонному дну к мелкому выпуклому берегу, а на поверхности течения — к вогнутому глубокому берегу (рис. 10). Поэтому лед в половодье и течение постоянно размывают вогнутые берега, течение увлекает наносы к выпуклым берегам, где они и оседают. Кроме того, внутреннее течение влияет на повышение уровня воды у вогнутого берега.
Внутреннее течение смежных живых сечений на изгибах русла реки образует винтообразное течение в потоке, направленное к яру, поверхностное течение которого называется прижимным течением. Оно сносит судно с курса в сторону вогнутого берега.
 Рис. 10. Внутреннее течение на изгибе русла: 1 — направление течения на поверхности — прижимное течение; 2 — направление течения на дне — донное течение
Рис. 10. Внутреннее течение на изгибе русла: 1 — направление течения на поверхности — прижимное течение; 2 — направление течения на дне — донное течение
При переходе от кривизны одного направления к другой (обращенной в другую сторону) винтообразное течение в изгибе
Русла меняет направление. На прямолинейном участке соединяющем эти два изгиба, винтообразное течение сначала рассеивается, а затем при новом изгибе снова сходится.
Одномерное движение
Одномерным называют движение системы с одной степенью свободы. Наиболее общий вид лагранжевой функции такой системы, находящейся в постоянных внешних условиях, есть
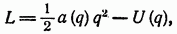
где  -некоторая функция обобщенной координаты q. В частности, если q есть декартова координата (назовем ее х),
-некоторая функция обобщенной координаты q. В частности, если q есть декартова координата (назовем ее х),
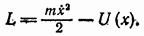
Соответствующие этим лагранжевым функциям уравнения движения интегрируются в общем виде. При этом нет даже необходимости выписывать самое уравнение движения, а следует исходить сразу из его первого интеграла — уравнения, выражающего закон сохранения энергии. Так, для функции Лагранжа (11,2) имеем:
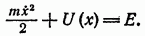
Это есть дифференциальное уравнение первого порядка, интегрирующееся путем разделения переменных. Имеем:
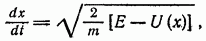
откуда
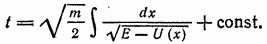
Роль двух произвольных постоянных в решении уравнения движения играют здесь полная энергия Е и постоянная интегрирования  .
.
Поскольку кинетическая энергия — величина существенно положительная, то при движении полная энергия всегда больше потенциальной, т. е. движение может происходить только в тех областях пространства, где 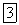 .
.
Пусть, например, зависимость  имеет вид, изображенный на рис. 6. Проведя на этом же графике горизонтальную прямую, соответствующую заданному значению полной энергии, мы сразу же выясним возможные области движения.
имеет вид, изображенный на рис. 6. Проведя на этом же графике горизонтальную прямую, соответствующую заданному значению полной энергии, мы сразу же выясним возможные области движения. 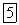 в изображенном на рис. 6 случае движение может происходить лишь в области АВ или в области справа от С.
в изображенном на рис. 6 случае движение может происходить лишь в области АВ или в области справа от С.
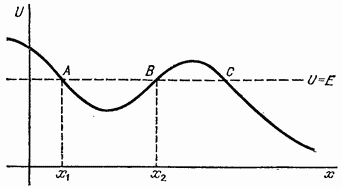
Рис. 6
Точки, в которых потенциальная энергия равна полной
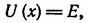
определяют границы движения. Они являются точками остановки, поскольку в них скорость обращается в нуль. Если область движения ограничена двумя такими точками, то движение происходит в ограниченной области пространства; оно является, как говорят, финитным. Если же область движения не ограничена или ограничена лишь с одной стороны, — движение инфинитно, частица уходит на бесконечность.
Одномерное финитное движение является колебательным — частица совершает периодически повторяющееся движение между двумя границами (на рис. 6 в потенциальной яме АВ между точками  ). При этом согласно общему свойству обратимости (стр. 18) время движения от
). При этом согласно общему свойству обратимости (стр. 18) время движения от  до
до  равно времени обратного движения от
равно времени обратного движения от  до
до  Поэтому период колебаний Т, т. е. время, за которое точка пройдет от
Поэтому период колебаний Т, т. е. время, за которое точка пройдет от  до
до  и обратно, равен удвоенному времени прохождения отрезка
и обратно, равен удвоенному времени прохождения отрезка  или согласно (11,3)
или согласно (11,3)
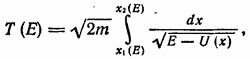
причем пределы  являются корнями уравнения (11.4) при данном значении Е. Эта формула определяет период движения в зависимости от полной энергии частицы.
являются корнями уравнения (11.4) при данном значении Е. Эта формула определяет период движения в зависимости от полной энергии частицы.
Задачи
1. Определить период колебаний плоского математического маятника (точка  на конце нити длиной I в поле тяжести) в зависимости от их амплитуды.
на конце нити длиной I в поле тяжести) в зависимости от их амплитуды.
Решение Энергия маятника 
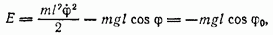
где  — угол отклонения нити от вертикали;
— угол отклонения нити от вертикали;  — максимальный угол отклонения. Вычисляя период как учетверенное время прохождения интервала углов от нуля до
— максимальный угол отклонения. Вычисляя период как учетверенное время прохождения интервала углов от нуля до  находим:
находим:
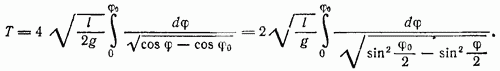
Подстановкой  этот интеграл приводится к виду
этот интеграл приводится к виду 
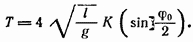
где
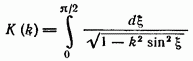
— так называемый полный эллиптический интеграл первого рода. При  (малые колебания) разложение функции
(малые колебания) разложение функции  дает:
дает:
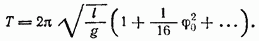
Первый член этого разложения отвечает известной элементарной формуле.
2, Определить период колебаний в зависимости от энергии при движении частицу массы  в полях с потенциальной энергией:
в полях с потенциальной энергией:
а) 
Ответ:
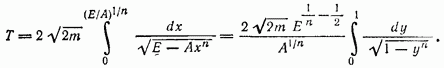
Подстановкой  интеграл приводится к так называемому
интеграл приводится к так называемому  -интеграу Эйлера; который выражается через Т-функции
-интеграу Эйлера; который выражается через Т-функции
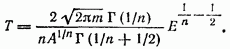
Зависимость Т от Е соответствует закону механического подобия (10.2), (10,3).
б) 
Ответ:
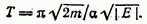
в) 
Ответ: