Проекцией вектора силы на ось называется скалярная величина, равная со знаком плюс или минус длине отрезка оси, заключённого между проекциями начала и конца данного вектора. Проекция считается положительной, если направление отрезка совпадает с положительным направлением оси, и отрицательной ― в противном случае.
Из рисунка видно, что проекции вектора силы на параллельные и одинаково направленные оси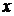 
и 
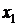будут одинаковы. Поэтому проекция 
равна с соответствующим знаком катету 
в прямоугольном треугольнике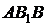 
:
.
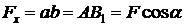Заметим, что эта формула остаётся справедливой и в случае, когда 
― тупой угол. В самом деле
.
Таким образом, проекция вектора силы на ось равна произведению модуля силы на косинус угла между силой и положительным направлением оси, причём
Очевидно, проекция вектора 
на ось 
равна с соответствующим знаком катету 
в прямоугольном треугольнике :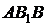
Алгебраическим моментом любой силы плоской системы сил относительно точки (центра), называется скалярная величина, равная со знаком плюс или минус произведению модуля силы на плечо.
mO (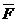
)= 
Fh
Договоримся о следующем правиле знаков
|
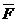
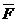
О О
mO(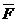)> 0 mO(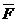) < 0
Перпендикуляр опущенный с центра моментов на линию действия силы называется плечом силы 
относительно 0.
Момент силы относительно точки равен нулю, если линия действия силы проходит через центр моментов (отсутствует плечо).
Если тело находится в равновесии под действием произвольной плоской системы сил, то силы, действующие на тело, должны удовлетворять трем условиям равновесия, которые можно записать в трех различных формах:
1-я (основная) форма условий равновесия.
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы сумма проекций всех сил на каждую из двух координатных осей и сумма моментов сил относительно любой точки, лежащей в плоскости действия сил, были равны нулю, то есть
∑ 
k =0; ∑ 
k =0; ∑ m 0 ( 
k) = 0.
2-я форма условий равновесия,
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы сумма моментов всех сил относительно каждой из двух произвольных точек, лежащих в плоскости действия сил, и сумма проекций всех сил на ось, не перпендикулярную к прямой, проходящей через эти точки, были равны нулю, то есть
∑mA ( k) = 0; ∑mB ( k) = 0; ∑ k =0.
3-я форма условий равновесия.
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы сумма моментов всех сил относительно каждой из трех произвольных точек в плоскости действия сил, не лежащих за одной прямой, была равна нулю, то есть
∑ mA ( k) = 0; ∑ mB ( k) = 0; ∑ mC ( k) = 0
Заметим, что число неизвестных в уравнениях равновесия произвольной плоской системы сил должно быть не более трех, чтобы задача была статически определимой.
Условия равновесия плоской системы параллельных сил можно записать в двух формах:
1-я (основная) форма условий равновесия.
Для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы сумма проекций всех сил на ось, параллельную силам, и сумма моментов всех сил относительно любой точки, лежащей в плоскости действия сил, были равны нулю, то есть
∑ k = 0; ∑ m 0 ( k) = 0.
2-я форма условий равновесия.
Для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы сумма моментов всех сил относительно каждой из двух произвольных точек, лежащих в плоскости действия сил так, что прямая, проходящая через эти точки, не параллельна силам, была равна нулю, то есть
∑ mA ( k) = 0; ∑ mB ( k) = 0.
Число неизвестных в этих уравнениях должно быть не более двух.
Методические указания к решению задач
Последовательность операций, указанных в практическом занятии № I, сохраняется и при решении задач на равновесие плоской системы сил.
Если в задаче заранее неизвестно направление какой-нибудь реакции, то эту реакцию следует представить в виде двух составляющих, направленных параллельно координатным осям в их положительную сторону.
Если в ходе решения задачи обнаружится, что величина какой-нибудь составляющей получится отрицательной, то это означает, что ее действительное направление противоположно выбранному на рисунке.
При решении задач желательно составлять такие уравнения равновесия, в каждое из которых входила бы только одна неизвестная величина. Для этого оси координат следует направлять перпендикулярно к неизвестным силам. За центр моментов следует брать точку пересечения линий действий двух неизвестных сил.
При решении задач на равновесие плоской системы параллельных сил ось координат целесообразно выбирать параллельно действующим силам, а центр моментов - на линии действия неизвестной силы.
Договоримся впредь не изображать на отдельном рисунке объект, освобожденный от связей. Все действующие силы будем указывать на рисунке с изображением данной конструкции.
Задача № 1 Из практикума № 7 (4.15 М)
Однородная балка АВ весом Р= 100 Н прикреплена к стене шарниром А и удерживается в равновесии под углом α = 450 к вертикали при помощи троса, перекинутого через блок С и несущего груз G. Ветвь троса ВС образует с вертикалью угол β =300. В точке D к балке подвешен груз Q весом 200Н.
О п р е д е л и т ь вес груза G и реакции шарнира А, пренебрегая трением, если В D = 
АВ.
Дано:
Р= 100 Н
α = 45 0
β =300.
Q = 200Н
В D = АВ
Определить: G, 
Р е ш е н и е
1. Объект равновесия: балка АВ.
Применяем аксиому связей
Всякое несвободное тело можно освободить от связей, заменив их действие реакциями, и рассматривать тело как свободное, находящееся под действием приложенных сил и реакций связи.
2. Силовая схема свободного объекта:
а) активные силы: 
- сила тяжести, приложенная посередине балки;
б) реакции связей: в точке А - ШНО (цилиндрический шарнир). Поскольку 
А заранее неизвестна по величине и направлению, то будем реакцию А изображать в виде двух составляющих 
А 
А, в точках В и D гибкая связь Реакции гибкой связи - 
, 
.
Даем характеристику системы:
S( , 
, 
А, А ) - произвольная плоская система сил, три неизвестных, можем составить три уравнения равновесия, задача является статически определимой
3. Условия равновесия.
Воспользуемся 1-й формой условий равновесия плоской системы сил. За центр моментов выберем точку А, работаем с правой системой координат.
∑ k = 0; – G sinβ + XA = 0;
∑ k = 0; G cosα – Q – P+ YA = 0;
∑mB ( k) = 0; - G AB sin(α + β) + Q 
sin α + P ∙ 
sinα = 0.
4. Решение уравнений.
Из последнего уравнения находим
G = (Q sin α + P ∙ sinα)/ sin (α + β); G = 146 кН.
Из второго уравнения получаем
YA = - G cosα + Q + P; YA = 173 кН.
Из первогоуравнения следует
XA = G sinβ; XA =73 кН.
