МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
Механические колебания – периодически повторяющиеся движения точки в 2-х противоположных направлениях.
Период – промежуток времени, в течение которого система совершает одно полное колебание:
, где N – число полных колебаний за время t.
Частота – число колебаний в единицу времени:
, 
, 
.
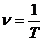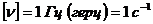Циклическая частота:
, 
.
Гармонические колебания – колебания, которые происходят по закону синуса (косинуса):
x = xmcos (ωt + φ 0), где
x – смещение тела от точки равновесия,
xm – амплитуда колебаний (максимальное смещение),
φ0 – начальная фаза,
(ω t + φ 0) – фаза колебания.
Скорость при φ0=0
υ=x´=-ωxmsinωt.
Ускорение при φ0=0
a=υ´=-ω2xmcosωt.
Свободные колебания – это колебания в системе под действием внутренних сил.
Математический маятник – материальная точка, подвешенная на невесомой нерастяжимой нити.
Период колебаний математического маятника:
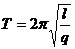, где l – длина маятника.
Период колебания пружинного маятника:
, где k – жёсткость пружины.
Вынужденные колебания – колебания, возникающие под действием периодически меняющейся внешней силы.
Механические волны – распространяющиеся колебания в упругой среде с течением времени.
Скорость волны – расстояние, которое за единицу времени проходит любая точка волновой поверхности.
Длина волны – расстояние, на которое волна распространяется за период:
λ=νT, [λ] =1м.
Контрольные вопросы
1. В каком положении на колеблющееся тело действует наибольшая возвращающаяся сила. Максимуму потенциальной или кинетической энергии они соответствуют.
2. Чем отличаются собственные колебания от свободных?
3. Что можно сказать о числовом значении скорости и ускорения в крайних положениях колеблющейся точки.
4. Колебание маятника в чесах относится к незатухающим. Чем это объясняется?
5. При каком условии возникает механический резонанс?
6. На Луне ускорение свободного падения в 6 раз меньше, чем на Земле. Как измениться период колебания математического маятника, если его перенести с Земли на Луна?
Примеры решения задач
Задача 1. Сколько колебаний совершает математический маятник длиной 4,9м за время 5мин?
| Дано: l =4,9м t=5мин | СИ: 3×102с |
| n -? |
Решение:
Период колебаний определяется по формуле 
Искомое число колебаний находим из отношения
Задача 2. Вертикально подвешенная пружина растягивается прикрепленным к ней грузом на величину D l =0,8см. Чему равен период свободных колебаний груза?
| Дано: D l= 0,8см | СИ: 8×10-3м |
| T -? |
Решение:
Период колебаний груза, прикрепленного к пружине, определяется формулой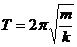 
На груз действует сила тяжести F Т. и сила упругости F упр . Условие равновесия груза – равенство сил по модулю: F Т.= F упр ., или
mg = k D l, отсюда 
Следовательно, 
Задача 3. Груз, прикрепленный к пружине, колеблется на горизонтальном гладком стержне. В некоторый начальный момент времени груз смещают от положения равновесия на 10см и отпускают. Определить координату груза через 1/8 периода колебаний.
Дано:
xm=10м
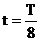
| СИ: 0,1м |
| x -? |
Решение:
Зависимость координат груза от времени выражается
x = xmcos 
× t,
поскольку 
и 
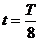, то 
;
Задача 4. Пользуясь графиком (рис.), запишите уравнение гармонических колебаний груза, закрепленного на пружине.
Решение:
Уравнение гармонических колебаний имеет вид: x = xm sin w t
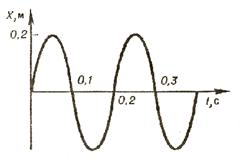По графику зависимости x (t) определяем, что амплитуда колебаний 0,2 м.
Для нахождения циклической частоты используем формулу 
; 
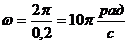
Тогда уравнение запишем x =0,2 sin 10 p t
Упражнения
1. Составить уравнение колебаний математического маятника, длина которого 2,45м, а амплитуда колебаний 10см.
Ответ: x=0,1 sin2t.
2. Колебание точки описывается уравнением x=0,05 cos20πt. Определить скорость точки через 1/60с после начала движения.
Ответ: -2,7м / с.
3. Определить ускорение свободного падения в некоторой местности, если нитяной маятник длиной 40см колеблется с той же частотой, что и пружинный массой 2000г на пружине с жёсткостью 49,1Н/м.
Ответ: 9,82м / с2.
4. К пружине динамометра подвесили груз, при этом указатель опустился на 2,5см. Какой будет частота колебания груза на этой пружине, если его вывести из состояния равновесия?
Ответ: 3,2Гц.
5. Координата груза маятника изменяется по закону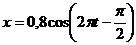 
. Изобразить колебания графически.
6. Один из маятников совершил 10 колебаний, а другой за то же время 6. Найти длину каждого маятника, если разность их длин 20см.
Ответ: 11,25см, 31,25см.
Самостоятельно
7. Записать уравнение гармонических колебаний по следующим данным: амплитуда 20см, начальная фаза π/4, частота колебаний 1Гц.
Ответ: 
8. Как относятся длины двух математических маятников, если за одно и тоже время один совершил 10 полных колебаний, а второй 20?
Ответ: l1/l2=4.
9. За какое время маятник отклонится от положения равновесия на половину амплитуды, если период его колебаний 3,6с?
Ответ: 0,3с.
10. Груз, массой 1000г, подвешен на пружине жёсткостью 0,1кН/м и совершает колебания с амплитудой 10см. Написать уравнение этих колебаний.
Ответ: x=0,1 sin10t.
11. Чему равна максимальная величина ускорения точки, движение которой описывается уравнением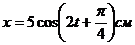 
.
Ответ: 0,2м / с2.
12. * Если к некоторому грузу, колеблющемуся на пружине, подвесить гирю 100г, то частота колебаний уменьшится в 1,4 раза. Какой массы груз был подвешен первоначально?
Ответ: 100г.
