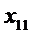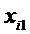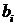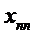Первую в истории оптимизационную задачу сформулировал Леонардо Фибоначчи, итальянский математик XIII века. Его задача "О гирях" посвящена проблеме взвешивания с помощью рычажных весов и создания оптимальной системы гирь для этой цели.
Задача о рюкзаке
Одно из первых упоминаний об этой задаче можно найти в статье Джорджа Балларда Мэтьюса, датированной 1897 годом.
Пусть имеется набор предметов, каждый из которых имеет два параметра – вес и ценность. И есть рюкзак, определенной вместимости. Задача заключается в том, чтобы собрать рюкзак с максимальной ценностью предметов внутри, соблюдая при этом весовое ограничение рюкзака. Дополнительно в задаче может быть оговорено максимальное количество предметов одного типа в рюкзаке (требование ассортимента).
В общем случае задача о рюкзаке бывает нескольких типов: простейший рюкзак (каждый предмет можно положить только в одном экземпляре), ограниченный рюкзак (каждый предмет кладется не более m раз), неограниченный рюкзак (каждый предмет можно укладывать сколько угодно раз), рюкзак с мультивыбором (все предметы разделены на S классов, обязательно вложить хотя бы один предмет каждого класса), мультипликативный рюкзак (имеется несколько рюкзаков, каждый со своей вместимостью) и многомерный рюкзак (у каждого предмета есть несколько характеристик, например, вес и объем, а у рюкзака – несколько ограничений).
Исходные данные к задаче представлены в табл. 15.2.
Табл. 15.2
| № предмета | Стоимость | Вес | Количество в рюкзаке |
| 1 | 
| 
| 
|
| 2 | 
| 
| 
|
| … | … | … | … |
| 
| 
| 
|
| … | … | … | … |
| 
| 
| 
|
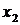
Здесь – количество предметов -го типа, которые нужно положить в рюкзак. – целое,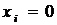 
для тех предметов, которые в рюкзак класть не имеет смысла, Суммарный вес вещей 
, суммарная их стоимость – 
.
В рассматриваемом случае должно соблюдаться условие 
, а также, при необходимости, 
, где m – максимальное количество вещей одного типа в рюкзаке, 
.
Целевая функция будет иметь вид 
.
Пример организации данных в таблице Microsoft Excel (целевая функция выделена красным) показан на рис. 15.11.
Рис. 15.11 Задача о рюкзаке
Транспортная задача
Эта задача была впервые формализована французским математиком Гаспаром Монжем в 1781 году.
Допустим, требуется составить план перевозок однородного груза таким образом, чтобы общая стоимость перевозок была минимальной. Исходные данные к задаче представлены в табл. 15.3.
Табл. 15.3
| Поставщики | Потребители | Запасы поставщиков | |||||||||
| 1 | 2 | … | j | … | n | ||||||
| 1 |
| 
|
| 
| … |
| 
| … |
| 
|
|
| 2 |
| 
|
| 
| … |
| 
| … |
| 
|
|
| … | … |
| … | … | … | … | … | ||||
| i |
| 
|
| 
| … |
| 
| … |
| 
|
|
| … | … | … | … | … | … | … | … | ||||
| m |
| 
|
| 
| … |
| 
| … |
| 
|
|
| Спрос потребителей |
|
| … |
| … |
| |||||
Здесь 
– количество единиц груза, которые нужно вывезти из i -го пункта отправления (
); 
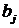– количество единиц груза, которое нужно привезти в j-й пункт назначения (
); – стоимость перевозки единицы груза из i -го пункта в j -й, зависит от расстояния между пунктами и некоторых других факторов. Обозначим через 
количество единиц груза для перевозки из i -го пункта в j -й. Тогда можно записать: общая (суммарная) стоимость перевозок 
; количество груза, вывозимого из i- го пункта 
; количество груза, доставляемого в j -й пункт 
. Количество вывезенного груза должно быть равно количеству принятого.
В рассматриваемом случае должны выполняться как минимум следующие условия (они будут ограничениями задачи): 
, 
; 
, 
; 
.
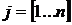Целевая функция представляет собой суммарную стоимость перевозок и имеет вид: 
.
Пример организации данных в таблице Microsoft Excel показан на рис. 15.12.
Рис. 15.12 Транспортная задача
Задача коммивояжера
Задача коммивояжёра (коммивояжёр – разъездной торговый агент) – одна из самых известных задач оптимизации, заключающаяся в отыскании самого выгодного маршрута, проходящего через указанные точки хотя бы по одному разу с последующим возвратом в исходную точку. Допустим, нам необходимо посетить каждую точку строго один раз. Исходные данные к задаче представлены в табл. 15.4.
Здесь – стоимость переезда из i -го пункта в j -й, зависит от расстояния между пунктами и некоторых других факторов. Обозначим через двоичную переменную факт переезда коммивояжера из пункта в пункт 
. 
, если перемещение имеет место, и 0, если нет. Тогда можно записать: общие (суммарные) затраты на разъезды 
.
Каждый из пунктов нужно посетить только один раз. Чтобы отследить этот факт, введем переменные – количество выездов из пункта i, , 
, и 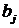– количество въездов в пункт j, 
, (). Величины и 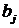должны быть равны 1 для всех i и j.
Решение задачи с такими условиями может привести к неверному результату, когда будет определено несколько непересекающихся оптимальных кольцевых маршрутов. Чтобы маршрут был один, приходится ввести еще одну проверку. Будем считать, что коммивояжер выезжает из пункта 1 (и возвращается в него же). Тогда можно ввести переменную 
, характеризующую очередность въезда в пункт j. Для пункта, в который коммивояжер приедет из пункта 1, 
будет равно 0, для следующего пункта – 1, и т.д. В этом случае существование единственного замкнутого маршрута будет описано условием 
, где 
, 
.
Табл. 15.4
| № пункта | № пункта | Количество въездов в пункт | |||||||||
| 1 | 2 | … | j | … | n | ||||||
| 1 |
| – |
|
| … |
|
| … |
|
|
|
| 2 |
|
|
| – | … |
|
| … |
|
|
|
| … | … |
| … | … | … | … | … | ||||
| i |
|
|
|
| … |
| – | … |
|
|
|
| … | … | … | … | … | … | … | … | ||||
| n |
| 
|
| 
| … |
| 
| … |
| – |
|
| Количество выездов из пункта |
|
| … |
| … |
| |||||
| Порядок посещения пункта | – |
| … |
| … |
| |||||
В рассматриваемом случае должны выполняться как минимум следующие условия (они будут ограничениями задачи): 
для всех 
; 
, ; 
, ; , , .
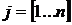Целевая функция представляет собой суммарные затраты на переезды и имеет вид: 
.
Пример организации данных в таблице Microsoft Excel показан на рис. 15.13.
Рис. 15.13 Задача коммивояжера
