2014-1. Все грани куба окрасили и этот куб распилили на тысячу кубиков одинакового размера. Сколько из них имеют хотя бы одну окрашенную грань?
♦ Ответ: 
Решение 1. Вычитаем из 
– общего числа кубиков 
число внутренних кубиков, у которых нет ни одной окрашенной грани.
Решение 2. Можно найти число кубиков с одной окрашенной гранью: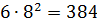 
, с двумя окрашенными гранями: 
, с тремя окрашенными гранями: 8. Хотя бы одну окрашенную грань имеют 
2014-2. Биссектриса угла треугольника делит противоположную сторону на части 
и 
. Разность двух других сторон равна 
. Найдите периметр треугольника.
♦ Ответ: 
если 
;
если 
если 
, где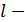 
любое число.
Если 
то треугольник равнобедренный. Пусть 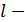его боковая сторона, тогда периметр равен 
Пусть 
Биссектриса делит противоположную сторону в отношении прилежащих сторон. Пусть 
коэффициент пропорциональности, тогда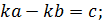 
. Полная запись ответа требует также эту формулу переписать для случая 
2014-3. Решите систему
♦ Ответ: (0; 0; 0), (-1;-1;-1)
Функция 
возрастающая, поэтому если 
, то
К равенству всех значений переменных приводит и предположение 
. Осталось решить уравнение 
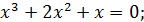
Ответ: (0; 0; 0), (–1;–1;–1).
2014-4. Пять красавиц ехали в Голливуд, каждая на своей машине. Англичанка ехала в синей машине. Итальянка была с собачкой. Египтянка была блондинкой. Испанка жевала Wrigleys. Немка ехала первой. В зелёной машине сосали конфеты. В голубой машине ехала шатенка. За жёлтой машиной ехала зелёная. Вторая машина была белая. В третьей машине глотали таблетки. Брюнетка была с котёнком. Во рту у рыжей торчала сигарета. В соседней с голубоволосой машине ехала лиса. Обезьяна ехала в машине соседней с шатенкой. С кем ехал попугай и кто пил кока-колу?
♦ Ответ: попугай ехал с египтянкой, а кока-колу пила немка
Решение можно начинать с таблицы. Некоторые клетки заполняются по условию задачи автоматически. Для пустой клетки высказываем предположение и анализ получившейся ситуации либо приводит к противоречию, либо приводит нас к убеждению, что так оно и есть. В результате получим такое заполнение таблицы:
| Националь-ность | Номер машины | Цвет машины | Цвет волос | Животное | Еда |
| Немка | 1 | голубой | Шатенка | обезьянка | кока-кола |
| Испанка | 2 | белый | голубоволосая | лиса | Wrigleys |
| Американка | 3 | синий | Брюнетка | котёнок | таблетки |
| Итальянка | 4 | жёлтый | Рыжая | собачка | сигарета |
| Египтянка | 5 | зелёный | Блондинка | попугай | конфеты |
2014-5. Докажите, что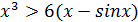 
для любых 
♦ Доказательство. Функция 
возрастающая (доказывается не так и просто!). Так как 
то выполняется неравенство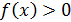 
для любых
2014-6. Найдите все значения параметра 
, при каждом из которых ни одно значение функции 
не принадлежит промежутку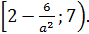 
♦ Ответ: 
Решение 1. Область значений 
функции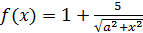 
не может находиться правее заданного промежутка, поэтому значения параметра находим из условия
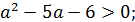
а так как , то
Решение 2. Значения параметра ищем из условия, что при них ни одно значение х не удовлетворяет цепочке неравенств
Пытаемся найти значения 
при которых для любого х выполняется неравенство
Для любого найдётся значение 
, при котором это неравенство не выполняется. Поэтому таких не существует.
Осталось найти значения при которых для любого х выполняется неравенство
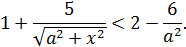
При 
имеем уже знакомое неравенство
Оно выполняется при фиксированном для всех х и даёт ответ
Так как область значений функции непрерывна, то случай, когда значения функции находятся и справа и слева от заданного промежутка, невозможен.
2014-7. Существуют ли многочлены 
и 
, для которых
при всех 
♦ Ответ: не существуют.
Равенство
невозможно, так как в нём слева рациональная дробь, а справа многочлен.
Можно сослаться на то, что два многочлена равны тогда и только тогда, когда равны все соответствующие коэффициенты. Равенство
невозможно, так как в нём слева многочлен степени 5, а слева степени 
2014-8. Решите уравнение
♦ Ответ: 
Решение 1. Перепишем уравнение в виде
Проявив наблюдательность, заметим, что его можно записать и так
с помощью функции
А так как эта функция оказалась возрастающей, то
Для его решения рассмотрим эквивалентное уравнение (возвели обе части в квадрат)
методом подбора найдём два корня и перепишем уравнение в виде
Решение уравнения свелось к решению квадратного уравнения
Решение 2. Перепишем уравнение в виде
Проявив наблюдательность, заметим, что
Отсюда,
Из первого уравнения
Далее как в первом решении.
2014-9. Математики известны как лучшие специалисты по информационной безопасности. Проявив упорство и наблюдательность, даже не зная криптографии, Вы должны, расшифровав текст, дать короткий и точный ответ на полученный вопрос
ПК ШП ПП ПШ ШШ ШК ПН НК ШИ ШК ШП КШ ИП УК КУ ИН КИ ШК ШН ШК ПН ПН ШУ ПП КУ ПН ШУ ПП КУ УК ИП ПН КП УН ШК ПН ШК ПУ ШН ПП УШ ШК ПШ ПП ШШ УК ПН НИ ШИ ШК ИП ПН ШУ КШ НН
♦ Ответ: расшифрованный текст:
ГЛАВНОЕ – ПОЛУЧИТЬ ХОРОШЕЕ МАТЕМАТИЧЕСКОЕ ОБРАЗОВАНИЕ. ПОЧЕМУ?
Проявив наблюдательность, заметим, что из букв текста складывается слово ПУШКИН. Соответствие букве сообщения пары букв наводит на мысль использовать систему координат. Каждой букве алфавита поставим в соответствие пару букв из таблицы:
| П | У | Ш | К | И | Н | |
| П | А | Б | В | Г | Д | Е |
| У | Ё | Ж | З | И | Й | К |
| Ш | Л | М | Н | О | П | Р |
| К | С | Т | У | Ф | Х | Ц |
| И | Ч | Ш | Щ | Ъ | Ы | Ь |
| Н | Э | Ю | Я | – | . | ? |
2014-10. Три шара радиуса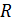 
касаются друг друга и заданной плоскости. Найдите радиус шара, который касается всех трёх шаров и плоскости.
♦ Ответ: 
Рассмотрим проекцию на касательную плоскость: 
проекции центров шаров,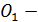 
проекция центра малого шара,
Проведём сечение через центр первого шара и малого шара перпендикулярно касательной плоскости. По теореме Пифагора
где 
радиус малого шара. Решив уравнение, найдём 
.
