8.1. В треугольнике 
высоты, опущенные на стороны 
и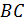 
, не меньше соответствующих сторон. Найдите углы этого треугольника.
♦ Пусть 
; 
Наклонная больше перпендикуляра, поэтому 
По условию 
Поэтому 
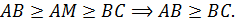Аналогично,
Получили 
треугольник прямоугольный и равнобедренный. Ответ: 
8.2. Найдите все пары целых чисел, для которых 
♦ Так как 
то возникают системы
Решим их. Ответ: (–5; –4), (–3; 0), (–5; 4), (5; 4), (5;–4), (3; 0).
8.3. При стрельбе по мишени спортсмен выбивал только по 8, 9 и 10 очков. Всего он сделал более 11 выстрелов и выбил 100 очков. Сколько выстрелов сделал спортсмен и какие были попадания?
♦ Ответ: 12 выстрелов при попаданиях 9 раз в 8, два раза в 9 и один раз в 10.
Пусть спортсмен выбил 
раз восьмёрку, 
раз девятку и 
раз десятку. 
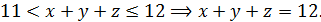Тогда 
.
8.4. Купец продал кафтан покупателю за 10 рублей. У него не было сдачи с 25 рублей. Он разменял 25-рублёвую купюру покупателя у соседа. Покупатель с покупкой ушёл. Сосед приходит: «Бумажка фальшивая». Пришлось купцу дать настоящую. Что потерял купец?
♦ Ответ: 15 + 25 = 40.
8.5. Лента, бесконечная вправо, разбита на клетки. На первой клетке сидит кузнечик. Из любой клетки кузнечик может перепрыгнуть либо на одну, либо на 2 клетки вправо. Сколькими способами кузнечик может добраться до десятой от начала клетки?
♦ Добраться до первой клетки можно одним способом – сидеть на месте. Существует только один способ добраться до второй клетки. До третьей клетки – 2 способа. До четвёртой – 3. До пятой – 5. В каждую следующую клетку кузнечик может попасть из попасть из предыдущей или либо перепрыгнув через неё поэтому число способов попасть в неё складывается из двух предыдущих чисел. Возникает последовательность 1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; … Ответ: 55.
9.1. Докажите, что уравнение 
не разрешимо в натуральных числах.
♦ Предположим, что нашлась тройка натуральных чисел, удовлетворяющих уравнению. Тогда все три равны друг другу не могут и без ограничения общности можно считать, что 
. Тогда 
или 
и сумма 
. Противоречие.
9.2. Функция называется нечётной, если 
для любого . Докажите, что 
функция нечётная.
♦ 
9.3. При каких значениях 
система 
не имеет решений?
♦ Ответ: 
При 
система несовместна 
Решим исходную систему при 
Вычтем из первого уравнения второе
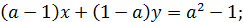
Решение 
системы существует при 
.
9.4. Сколькими способами можно разложить 5 монет различного достоинства по трём карманам?
♦ Ответ: 
. Каждую монету можно положить в любой карман тремя способами: в первый карман, во второй карман или в третий карман. Одну монету можно разложить тремя способами, две – девятью; три – 
четыре – 
; пять – 
способами.
9.5. Окружность с центром О вписана в прямоугольный треугольник 
, 
– еёпроекция на гипотенузу 
Найдите угол 
♦ Пусть 
точка касания окружности гипотенузой и 
радиус окружности. Тогда 
прямоугольный равнобедренны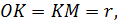й, 
и 
, аналогично, 
. Ответ. 
10.1. Решите в натуральных числах уравнение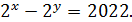 
♦ 
Ответ: 
10.2. Постройте квадрат, три вершины которого лежат на трёх данных параллельных прямых.
♦ Анализ. Даны три параллельные прямые 
и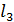 
(перечисляем снизу вверх). Предположим, что 
вершина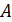 
искомого квадрата лежит на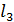 
, 
на , 
на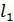 
. Вокруг вершины 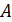повернём точку на 
по часовой стрелке. Тогда точка перейдёт в точку 
.
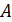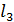Построение. Выберем произвольно точку на прямой . Повернём прямую по часовой стрелке на вокруг точки 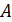. Полученная прямая пересечется с прямой 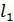в точке . Повернув точку в обратном направлении, на прямой 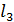получим точку . Равнобедренный прямоугольный треугольник 
достроим до квадрата . Квадрат искомый.
10.3. Окружность с центром О радиуса 
вписана в прямоугольный треугольник , – еёпроекция на гипотенузу Найдите радиус окружности, описанной около треугольника 
♦ радиус окружности, вписанной в треугольник 
точка касания окружности гипотенузой. Треугольник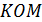 
прямоугольный равнобедренный, ,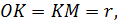 
; аналогично, 
Оказалось, что О – центр окружности, описанной около треугольника MCN. Ответ. 
10.4. Сто учеников сидят за круглым столом, причём более половины из них мальчики. Докажите, что какие-то два мальчика сидят друг напротив друга.
♦ Предположим противное, тогда в каждой из пятидесяти пар есть девочка. Мальчиков должно быть 
Противоречие с условием.
10.5. При каких значениях параметра система уравнений
имеет единственное решение?
♦ Ответ: 
Если 
решение системы, то 
тоже решение системы. Поэтому, если решение единственное, то 
т. е. получаем систему
которая распадается на две системы
и 
При 
исходная система, кроме 
, имеет ещё решения: 
. Докажем, что при 
кроме (0; 1), нет других решений системы
Из условия 
следует, что 
Первое из этих неравенств даёт 
Вместе с тем с тем, что 
это даёт нам 
Получили то же самое решение, т. е. оно единственное.
11.1 Докажите, что если число 
делится на 
, то 
простое
число.
♦ Предположим противное, что представимо в виде произведения двух натуральных чисел, 
Тогда 
, и присутствует среди множителей 
т. е. при некотором натурально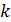м 
имеем
Единица делится на натуральное число, отличное от 1. Противоречие.
11.2. Числа 
и образуют решение системы
.
Докажите, что хотя бы одно из них равно .
♦ Из второго уравнения системы следует, что 
Поэтому
Так как 
то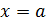 
или 
или 
11.3. Сторона основания правильной треугольной призмы 
равна 2, а диагональ боковой грани 
. Найдите угол между плоскостью 
и плоскостью основания.
♦ Если 
середина 
то 
и 
перпендикулярны следовательно, 
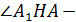линейный угол другранного угла с гранями 
и 
. Так как 
из треугольника 
и 
из треугольника 
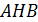, то 
. Ответ: 
11.4. Окружность вписана в прямоугольный треугольник , – еёпроекция на гипотенузу Найдите угол
♦ Введём обозначения: 
центр окружности, радиус, 
точка окружности, которая проектируется на 
, 
точка пересечения прямой 
со стороной 
точка касания окружности прямой 
Тогда 
Как отрезки касательных к окружности, проведённые из одной точки, 
А так как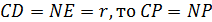 
. Треугольник 
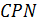равнобедренный с внешним углом 
при вершине Р. Поэтому 
. Аналогично, 
, поэтому 
Ответ.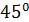 
Решение 2. Так как 
, то центр окружности, описанной около треугольника В ней центральный угол 
, поэтому вписанный угол 
11.5 При каких натуральных 
и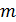 
имеет корни уравнение
?
♦ Ответ: уравнение имеет корни, если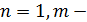 
любое натуральное число, или, если 
, или, если 
К уравнению 
применим метод дополнительного угла; введём угол, для которого
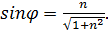
Тогда уравнение принимает вид
Уравнение имеет корни, если
Если 
, то это неравенство выполняется для любого натурального . Если 
то перепишем неравенство в виде 
или 
. Если 
, то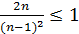 
и возможно только одно значение 
. При 
возможны или 
При 
возможно только .
