8.1. Докажите, что при натуральном  число
число  не может быть равно нулю.
не может быть равно нулю.
♦ Решение 1. Если бы такое  нашлось, то оно должно быть делителем числа 31 =
нашлось, то оно должно быть делителем числа 31 =  , т. е.
, т. е.  или
или  . Но они числа 31 не дают.
. Но они числа 31 не дают.
Решение 2. Если  чётно, то сумма чётного числа
чётно, то сумма чётного числа  , и нечётного числа 31 даёт число нечётное, которое не может равняться чётному числу 0. Если
, и нечётного числа 31 даёт число нечётное, которое не может равняться чётному числу 0. Если  нечётно, то сумма трёх нечётных чисел
нечётно, то сумма трёх нечётных чисел  нечётна и поэтому не может равняться чётному числу 0.
нечётна и поэтому не может равняться чётному числу 0.
8.2. При каких значениях  уравнение
уравнение  имеет два различных корня?
имеет два различных корня?
♦ Если  то корень
то корень  . Если
. Если  то корни совпадают
то корни совпадают  . В остальных случаях два неравных корня
. В остальных случаях два неравных корня 
8.3. За круглым столом сидят 4 гнома. Перед каждым стоит кружка с молоком. Один из громов переливает  своего молока соседу справа. Затем сосед справа делает то же самое. Затем то же самое делает следующий сосед справа. И, наконец, четвёртый гном
своего молока соседу справа. Затем сосед справа делает то же самое. Затем то же самое делает следующий сосед справа. И, наконец, четвёртый гном  оказавшегося у него молока наливает первому. Во всех кружках вместе молока 2 л. Сколько молока было первоначально в кружках, если в конце концов у всех гномов молока оказалось поровну?
оказавшегося у него молока наливает первому. Во всех кружках вместе молока 2 л. Сколько молока было первоначально в кружках, если в конце концов у всех гномов молока оказалось поровну?
♦ 


8.4. На окружности заданы точки  Отрезок
Отрезок  диаметр окружности. Из точек
диаметр окружности. Из точек 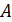 и
и  на прямую
на прямую  опущены перпендикуляры
опущены перпендикуляры  и
и  соответственно. Докажите, что
соответственно. Докажите, что 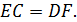
♦ Пусть М – основание перпендикуляра, опущенного из центра окружности О на хорду  Тогда
Тогда 
8.5. Крестьянин купил стадо, состоящее из свиней, коз и овец – всего 100 голов. Он заплатил за стадо 100 крон. За каждую свинью по 3,5 кроны. За каждую козу по  кроны. За каждую овцу по 0,5 кроны. Сколько свиней, коз и овец купил крестьянин?
кроны. За каждую овцу по 0,5 кроны. Сколько свиней, коз и овец купил крестьянин?
♦ Ответ: Три варианта покупки свиней, коз и овец (5; 42; 53), (10; 24; 66) и (15; 6; 79). Если крестьянин купил  свиней,
свиней,  коз и
коз и  овец, то задача свелась к решению системы
овец, то задача свелась к решению системы


Из второго вычтем первое, умноженное на 3:

9.1. Для некоторых целых  и
и  число
число  делится на 23. Докажите, что число
делится на 23. Докажите, что число 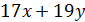 также делится на 23.
также делится на 23.
♦ Решение 1. По условию  . Дополнив 17 до 23, получим
. Дополнив 17 до 23, получим

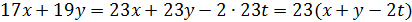
делится на 23.
Решение 2. Если обратим внимание на 3 х =  , то получим
, то получим
 .
.
Из того, что  делится на 23, следует, что
делится на 23, следует, что 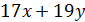 также делится на 23.
также делится на 23.
9.2. Функция называется нечётной, если  для любого
для любого  . Докажите, что
. Докажите, что  функция нечётная.
функция нечётная.
♦ Решение 1.


Решение 2.

9.3. В конференции принимает участие 77 человек. Может ли каждый из них быть знаком ровно с семью другими?
♦ Предположим, что может. Тогда в числе  каждый участник учтён дважды. Оно должно быть чётным. Противоречие. Значит, наше предположение неверно.
каждый участник учтён дважды. Оно должно быть чётным. Противоречие. Значит, наше предположение неверно.
9.4. Решите систему

♦ Ответ: (3; 1), (1; 3), (–3;–1), (–1;–3).
Решение 1. Заметим, что если пара  образует решение системы, то
образует решение системы, то  и
и  ,
,  и
и  – тоже решения. Поэтому можно искать решения, для которых
– тоже решения. Поэтому можно искать решения, для которых  и из них получать остальные.
и из них получать остальные.




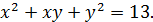



Решение 2. Возведя в квадрат обе части уравнения

получим







9.5. Окружность с центром О радиуса  вписана в прямоугольный треугольник
вписана в прямоугольный треугольник 
 ,
,  – еёпроекция на гипотенузу
– еёпроекция на гипотенузу  Найдите радиус окружности, описанной около треугольника
Найдите радиус окружности, описанной около треугольника 
♦ Пусть  точка касания окружности гипотенузой. Тогда
точка касания окружности гипотенузой. Тогда  Ответ.
Ответ. 
10.1. Докажите, что при  числа
числа  и
и  не могут быть простыми одновременно.
не могут быть простыми одновременно.
♦ Решение 1. Среди трёх последовательных целых чисел  одно делится на 3, но это не
одно делится на 3, но это не  , поэтому
, поэтому  или
или  . Значит, одно из них делится на 3, а так как оно не равно трём, то составное.
. Значит, одно из них делится на 3, а так как оно не равно трём, то составное.
Решение 2.  Произведение делится на 3, поэтому одно из них составное – делится на 3.
Произведение делится на 3, поэтому одно из них составное – делится на 3.
Решение 3. Если  составное,
составное,  то
то  число составное:
число составное: 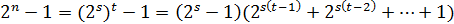 . Если
. Если  простое,
простое,  то
то  нечётное и
нечётное и  составное:
составное:  , делится на 3. Поэтому при
, делится на 3. Поэтому при  числа
числа  и
и  не могут быть простыми одновременно.
не могут быть простыми одновременно.
Решение 4. Предположим противное: нашлось 
 . Из того, что
. Из того, что  простое, следует, что
простое, следует, что  тоже простое. Из того, что
тоже простое. Из того, что  простое, следует, что
простое, следует, что  . Простое число представимо в виде степени двойки
. Простое число представимо в виде степени двойки  только если эта степень первая,
только если эта степень первая,  . Противоречие с тем, что
. Противоречие с тем, что  .
.
Полезные формулы

Если  нечётное, то
нечётное, то

Решение 5. При  эти числа не равны 2 и 3. Простое число, отличное от 2 и 3 можно представить в виде
эти числа не равны 2 и 3. Простое число, отличное от 2 и 3 можно представить в виде  Если
Если  то
то  делится на 3. Если
делится на 3. Если  то
то  на 3. Противоречие...
на 3. Противоречие...
Решение 6. Методом полной математической индукции можно доказать, что при  одно из чисел
одно из чисел  или
или  делится на 3. Если
делится на 3. Если  , то
, то  делится на 3. Если
делится на 3. Если  , то
, то  делится на 3.
делится на 3.
10.2. Решите уравнение 
♦ Ответ: 
Решение 1. После возведения в квадрат получим

Заметив, что  удовлетворяет этому уравнению, получим
удовлетворяет этому уравнению, получим
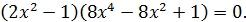
Осталось решить биквадратное уравнение. Проверка обязательна.
Решение 2. Замена  приводит уравнение к виду
приводит уравнение к виду 

10.3. Дана система уравнений

Два человека выписывают по очереди вместо звёздочек числа. Докажите, что начинающий всегда может добиться того, чтобы система имела ненулевое решение.
♦ Начинающий всегда может добиться того, чтобы получить решение (1; 1; 1)
Для этого, он своими ходами каждое уравнение приводит к одному из видов

или 
или  .
.
Очень эффектна стратегия, когда он получает решение (0;1;–1).
Для этого он систему приводит к виду

Первым ходом ставит 0 в левом верхнем углу, а затем во втором и третьем столбцах ставит то же число, что и его партнёр!
Он может получить решение (0; 1; 1), если систему приведёт к виду

10.4. Каждая сторона треугольника  разделена на 8 равных отрезков. Сколько существует различных треугольников с вершинами в точках деления (точки
разделена на 8 равных отрезков. Сколько существует различных треугольников с вершинами в точках деления (точки  не могут быть вершинами треугольников), у которых ни одна сторона не параллельна ни одной из сторон треугольника
не могут быть вершинами треугольников), у которых ни одна сторона не параллельна ни одной из сторон треугольника  ?
?
♦ Ответ: 216. Всего треугольников с вершинами в этих точках  Треугольников, у которых одна сторона параллельна одной из трёх сторон исходного треугольника
Треугольников, у которых одна сторона параллельна одной из трёх сторон исходного треугольника 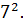 Треугольников, у которых две стороны параллельны двум сторонам исходного 7. У одного треугольника все три стороны параллельны сторонам исходного. Отсюда, ответ
Треугольников, у которых две стороны параллельны двум сторонам исходного 7. У одного треугольника все три стороны параллельны сторонам исходного. Отсюда, ответ

10.5. Найдите все значения  , при каждом из которых уравнение имеет хотя бы один корень
, при каждом из которых уравнение имеет хотя бы один корень

♦ Запишем равнение в виде  Функция
Функция

непрерывна. После раскрытия модулей

При 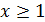 она возрастает, так как при любом раскрытии модулей
она возрастает, так как при любом раскрытии модулей

имеем 
При  функция убывает, так как при любом раскрытии модулей
функция убывает, так как при любом раскрытии модулей

имеем  .
.
Следовательно, наименьшее значение функция принимает при х = 1, а уравнение 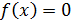 имеет хотя бы один корень тогда и только тогда, когда
имеет хотя бы один корень тогда и только тогда, когда  Решим это неравенство
Решим это неравенство




Ответ: 
11.1. Найдите все такие пары взаимно простых натуральных чисел  и
и  , что если к десятичной записи числа
, что если к десятичной записи числа  приписать справа через запятую десятичную запись числа
приписать справа через запятую десятичную запись числа  , то получится десятичная запись числа, равного
, то получится десятичная запись числа, равного  .
.
♦ По условию  где
где  количество цифр в числе
количество цифр в числе  . Тогда
. Тогда 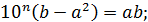
 Так как числа
Так как числа  и
и  взаимно простые, то
взаимно простые, то  и
и  тоже взаимно простые. Поэтому
тоже взаимно простые. Поэтому  ,
, 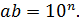 А это возможно в двух случаях. В первом случае
А это возможно в двух случаях. В первом случае  тогда
тогда 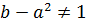 . Противоречие. Во втором случае
. Противоречие. Во втором случае  Тогда равенство
Тогда равенство  примет вид
примет вид 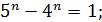
 . В этом уравнении слева функция возрастающая, а справа убывающая. Такое уравнение имеет не более одного корня. Единственный корень
. В этом уравнении слева функция возрастающая, а справа убывающая. Такое уравнение имеет не более одного корня. Единственный корень  . Ответ:
. Ответ: 
11.2. Числа  и
и  образуют решение системы
образуют решение системы
 .
.
Докажите, что хотя бы одно из них равно  .
.
♦ Требуется доказать, что  или
или  или
или  . Следовательно, надо доказать, что
. Следовательно, надо доказать, что  или
или  или
или  Иначе говоря, надо доказать, что
Иначе говоря, надо доказать, что  А это действительно так:
А это действительно так:
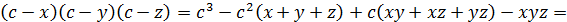

Здесь мы воспользовались тем, что из второго уравнения системы  а из первого
а из первого 
Так как  то
то  или
или  или
или 
11.3. В треугольнике  угол
угол  равен
равен  На стороне
На стороне  взята точка
взята точка  , для которой
, для которой  и
и  Найдите радиус окружности, проходящей через точки
Найдите радиус окружности, проходящей через точки  и касающейся прямой
и касающейся прямой 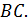
♦ Ответ: 1 или 7. Два ответа возникают в связи с тем, что точка касания может находиться на прямой 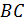 по одну сторону с точкой
по одну сторону с точкой  относительно
относительно  или по разные.
или по разные.
Пусть точка  касания окружности с прямой
касания окружности с прямой 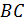 лежит на луче
лежит на луче 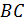 . По теореме о касательной и секущей
. По теореме о касательной и секущей
 .
.
Пусть  точка пересечения луча
точка пересечения луча  и перпендикуляра к
и перпендикуляра к 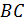 , проведённого через точку
, проведённого через точку  . Из прямоугольного треугольника
. Из прямоугольного треугольника  находим
находим


Следовательно,  центр искомой окружности, а её радиус равен 1.
центр искомой окружности, а её радиус равен 1.
Пусть теперь точка  касания окружности с прямой
касания окружности с прямой 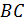 лежит на продолжении
лежит на продолжении 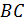 за точку
за точку  , а прямая, проходящая через точку
, а прямая, проходящая через точку  перпендикулярно
перпендикулярно 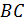 , пересекает прямую
, пересекает прямую  в точке
в точке  а окружность вторично – в точке
а окружность вторично – в точке  Тогда
Тогда


Если  радиус окружности, то
радиус окружности, то  По теореме о двух секущих
По теореме о двух секущих 

11.4. В последовательности  каждое следующее число получается из предыдущего по формуле
каждое следующее число получается из предыдущего по формуле 
Найдите 
♦ Ответ:  Значения повторяются через четыре номера
Значения повторяются через четыре номера
 ;
; 

11.5. При каких натуральных  и
и 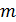 имеет корни уравнение
имеет корни уравнение
 ?
?
♦ Ответ: уравнение имеет корни, если  любое натуральное число, или, если
любое натуральное число, или, если  , или, если
, или, если 
Решение 1. Пусть  Уравнение
Уравнение  имеет корни при любом натуральном
имеет корни при любом натуральном  При
При  имеем уравнение
имеем уравнение  , которое при
, которое при  не имеет корней. Уравнения
не имеет корней. Уравнения  и
и  корни имеют. При
корни имеют. При 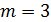 имеем уравнение
имеем уравнение  , которое, очевидно, при
, которое, очевидно, при  не имеет корней. При
не имеет корней. При  имеем уравнение, которое также при
имеем уравнение, которое также при  не имеет корней.
не имеет корней.
Решение 2. К уравнению
 ;
;
применим метод введения дополнительного угла; введём угол, для которого


Тогда уравнение принимает вид
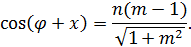
Уравнение имеет корни, если

Если  , то это неравенство выполняется при любом натуральном
, то это неравенство выполняется при любом натуральном  . Если
. Если 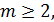 то перепишем неравенство в виде
то перепишем неравенство в виде  или
или 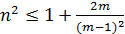 . При
. При  возможны
возможны  или
или  При
При 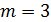 возможно только
возможно только  . Если
. Если  , то
, то  и возможно только одно значение
и возможно только одно значение  .
.






