ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
ШКОЛА ЕСТЕСТВЕННЫХ НАУК
МАЛАЯ АКАДЕМИЯ ШЕН ДВФУ "ПУТЬ К УСПЕХУ"
МАТЕРИАЛЫ МАТЕМАТИЧЕСКИХ
ОЛИМПИАД В ПРИМОРСКОМ КРАЕ
Год
Владивосток 2014
МУНИЦИПАЛЬНЫЙ ЭТАП
ВСЕРОССИЙСКОЙ ОЛИМПИАДЫ ПО МАТЕМАТИКЕ
Владивосток, 29 ноября 2014 года
Класс
1. Докажите, что при натуральном 
число 
не может быть равно нулю.
2. При каких значениях 
уравнение 
имеет два различных корня?
3. За круглым столом сидят 4 гнома. Перед каждым стоит кружка с молоком. Один из громов переливает 
своего молока соседу справа. Затем сосед справа делает то же самое. Затем то же самое делает следующий сосед справа. И, наконец, четвёртый гном оказавшегося у него молока наливает первому. Во всех кружках вместе молока 2 л. Сколько молока было первоначально в кружках, если в конце концов у всех гномов молока оказалось поровну?
4. На окружности заданы точки 
Отрезок 
диаметр окружности. Из точек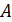 
и 
на прямую 
опущены перпендикуляры 
и 
соответственно. Докажите, что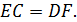 
5. Крестьянин купил стадо, состоящее из свиней, коз и овец – всего 100 голов. Он заплатил за стадо 100 крон. За каждую свинью по 3,5 кроны. За каждую козу по 
кроны. За каждую овцу по 0,5 кроны. Сколько свиней, коз и овец купил крестьянин?
МУНИЦИПАЛЬНЫЙ ЭТАП
ВСЕРОССИЙСКОЙ ОЛИМПИАДЫ ПО МАТЕМАТИКЕ
Владивосток, 22 ноября 2014 года
Класс
1. Для некоторых целых 
и 
число 
делится на 23. Докажите, что число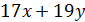 
также делится на 23.
2. Функция называется нечётной, если 
для любого . Докажите, что 
функция нечётная.
3. В конференции принимает участие 77 человек. Может ли каждый из них быть знаком ровно с семью другими?
4. Решите систему
5. Окружность с центром О радиуса 
вписана в прямоугольный треугольник 
, 
– еёпроекция на гипотенузу 
Найдите радиус окружности, описанной около треугольника 
МУНИЦИПАЛЬНЫЙ ЭТАП
ВСЕРОССИЙСКОЙ ОЛИМПИАДЫ ПО МАТЕМАТИКЕ
Владивосток, 15 ноября 2014 года
Класс
1. Докажите, что при 
числа 
и 
не могут быть простыми одновременно.
2. Решите уравнение 
3. Дана система уравнений
Два человека выписывают по очереди вместо звёздочек числа. Докажите, что начинающий всегда может добиться того, чтобы система имела ненулевое решение, т. е. в котором хотя бы одно число отлично от нуля.
4. Каждая сторона треугольника разделена на 8 равных отрезков. Сколько существует различных треугольников с вершинами в точках деления (точки 
не могут быть вершинами треугольников), у которых ни одна сторона не параллельна ни одной из сторон треугольника ?
5. Найдите все значения , при каждом из которых уравнение имеет хотя бы один корень 
МУНИЦИПАЛЬНЫЙ ЭТАП
ВСЕРОССИЙСКОЙ ОЛИМПИАДЫ ПО МАТЕМАТИКЕ
