8.1. На прямой выбраны точки  и
и  на расстоянии 10.Где на прямой находится точка
на расстоянии 10.Где на прямой находится точка  , если длина отрезка
, если длина отрезка  в полтора раза больше длины отрезка
в полтора раза больше длины отрезка 
♦ Пусть точка  лежит между
лежит между  и
и  . Тогда, очевидно,
. Тогда, очевидно,  ,
, 
 Если точка
Если точка  лежит на прямой
лежит на прямой  за точкой
за точкой  то
то  Пусть точка
Пусть точка  лежит на прямой
лежит на прямой  за точкой
за точкой  и
и 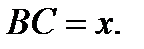 Тогда
Тогда 



 В первом случае говорят, что точка
В первом случае говорят, что точка  делит отрезок
делит отрезок  внутренним образом, а во втором – внешним.
внутренним образом, а во втором – внешним.
Ответ. Точка  может лежать между
может лежать между  и
и  . Тогда
. Тогда  ,
,  Точка
Точка  может лежать на прямой
может лежать на прямой  за точкой
за точкой  . Тогда
. Тогда 

8.2. Обыкновенная дробь  называется сократимой, если её можно сократить, то есть нацело разделить числитель и знаменатель на одно и то же целое число, больше 1. При каких
называется сократимой, если её можно сократить, то есть нацело разделить числитель и знаменатель на одно и то же целое число, больше 1. При каких 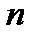 и на что можно сократить дробь
и на что можно сократить дробь 
♦ Предположим дробь сократима на натуральное число 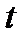 . Тогда
. Тогда 
 Откуда
Откуда 
 делитель числа 6,
делитель числа 6,  или 6. Если
или 6. Если  то
то 

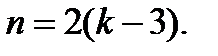 Если
Если  то
то 

 Если
Если  то
то 

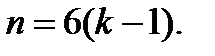
Ответ.  может равняться
может равняться 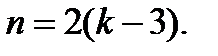
 Дробь
Дробь 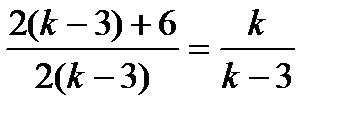 сократима на 2.
сократима на 2.
 может равняться
может равняться 
 . Дробь
. Дробь  сократима на 3 и
сократима на 3 и  может равняться
может равняться 
 Дробь
Дробь  сократима на 6.
сократима на 6.
8.3. В последовательности 1; 1; 2; 3; 5; 8; 13; 21; … каждое следующее число равно сумме двух предыдущих. Могут ли в ней оказаться рядом два чётных числа?
♦ Нет. Тогда все предыдущие должны быть чётными. А это не так.
8.4. Царь выделял на содержание всего писарского приказа 1000 рублей в год (все писари получали поровну). Царю посоветовали сократить численность писарей на 50 %, а оставшимся писарям повысить жалованье на 50 %. На сколько изменятся при этом затраты царя на писарский приказ?
♦ Если писарей было  , то каждый писарь получал
, то каждый писарь получал  рублей. Если писарей станет
рублей. Если писарей станет  , а жалование каждого писаря станет
, а жалование каждого писаря станет  рублей, то затраты царя станут
рублей, то затраты царя станут  = 750 рублей. Затраты сократятся на 250 рублей. Ответ. Затраты сократятся на 25 %.
= 750 рублей. Затраты сократятся на 250 рублей. Ответ. Затраты сократятся на 25 %.
8.5. В мешочке лежат 128 конфет. Играют двое, ходят по очереди. За один ход каждый может взять себе любое количество конфет. Но надо соблюдать два правила. Правило вежливости – нельзя брать конфет больше, чем только что взял противник. Правило честности – самым первым ходом в игре нельзя брать сразу все конфеты. Кто выиграет при правильной игре и заберёт себе все конфеты: начинающий или его партнёр?
♦ Если в пакете 2 леденца, то первый берёт один; второй тоже берёт один и побеждает. Если в пакете 4 леденца, и первый взял один леденец, то дальше по очереди они могут брать только по одному леденцу, и выигрыш у второго. Если первый взял два или три леденца, то второй забирает остальные и побеждает. После разбора случая восьми леденцов, а при необходимости 16 и т. д., становится ясно, что если первый возьмёт половину или больше леденцов, то проиграет; если игрок оставит нечётное число леденцов, то проиграет… Ответ. Выигрывает партнёр начинающего.
9.1. Найдите все целые числа  , для которых
, для которых  делится на
делится на  .
.
♦  Отсюда, 2 делится на
Отсюда, 2 делится на  . Поэтому
. Поэтому  равно
равно  или
или  Ответ. 0; 1.
Ответ. 0; 1.
9.2. Обыкновенная дробь  называется сократимой, если её можно сократить, то есть нацело разделить числитель и знаменатель на одно и то же целое число, больше 1. При каких
называется сократимой, если её можно сократить, то есть нацело разделить числитель и знаменатель на одно и то же целое число, больше 1. При каких 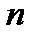 и на что можно сократить дробь
и на что можно сократить дробь 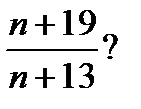
♦ Предположим дробь сократима на натуральное число 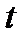 . Тогда
. Тогда 
 Откуда
Откуда 
 делитель числа 6,
делитель числа 6,  или 6. Если
или 6. Если  то
то 

 Если
Если  то
то 

 Если
Если  то
то 


Ответ.  может равняться
может равняться 
 Дробь
Дробь  сократима на 2.
сократима на 2.
 может равняться
может равняться 
 . Дробь
. Дробь  сократима на 3.
сократима на 3.
 может равняться
может равняться 
 Дробь
Дробь  сократима на 6.
сократима на 6.
9.3. Пусть  скорость лыжника на спуске,
скорость лыжника на спуске,  – на подъёме,
– на подъёме,  – длина подъёма, тогда
– длина подъёма, тогда  – длина спуска.
– длина спуска. 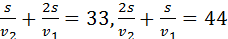 ;
;
 =
= 
♦ Ответ. В 2,5 раза.
9.4. Земной шар обвязали по экватору верёвкой. Затем верёвку удлинили на метр и приподняли над экватором так, что образовалась щель постоянной ширины. Сможет ли в эту щель пролезть кошка?
♦Ширина щели  см для кошки не проблема.
см для кошки не проблема.
9.5. Диагонали разрезают четырёхугольник на четыре треугольника. Назовём два из них противоположными, если у них есть общая вершина, но нет общих сторон. Четырёхугольник является трапецией тогда и только тогда, когда найдутся два противоположных треугольника, у которых площади равны. Докажите.
♦ 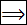 Пусть
Пусть 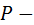 точка пересечения диагоналей трапеции
точка пересечения диагоналей трапеции  . Так как треугольников
. Так как треугольников  и
и  основание
основание  общее, а высоты равны, то площади треугольников равны.
общее, а высоты равны, то площади треугольников равны.

Доказано, что в трапеции два противоположных треугольника равновелики.

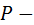 точка пересечения диагоналей четырёхугольника
точка пересечения диагоналей четырёхугольника  Пусть
Пусть  Тогда
Тогда  так как
так как  Площади треугольников равны, основание общее, поэтому у них высоты равны. Это означает, что
Площади треугольников равны, основание общее, поэтому у них высоты равны. Это означает, что  . Четырёхугольник
. Четырёхугольник  трапеция.
трапеция.
10.1. Сумма двух целых чисел равна их произведению. Найдите эти числа.
♦ Надо решить в целых числах уравнение  Перепишем его так:
Перепишем его так:  Или
Или  В левой части вынесем общий множитель
В левой части вынесем общий множитель  за скобки
за скобки  Отсюда, либо
Отсюда, либо  либо
либо  Ответ. (0; 0), (2; 2).
Ответ. (0; 0), (2; 2).
10.2. Решите уравнение 
♦ Ясно, что  Разделив обе части уравнение на
Разделив обе части уравнение на  приведём его к виду
приведём его к виду  Так как
Так как  а
а  то
то 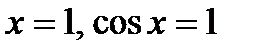 или
или 
Ответ. Корней нет.
10.3. Диагонали разрезают четырёхугольник на четыре треугольника. Назовём два из них противоположными, если у них есть общая вершина, но нет общих сторон. Произведение площадей двух противоположных треугольников равно произведению площадей двух других противоположных треугольников. Докажите.
♦ Пусть 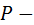 точка пересечения диагоналей трапеции
точка пересечения диагоналей трапеции  и
и 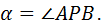
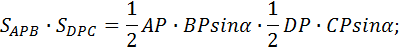
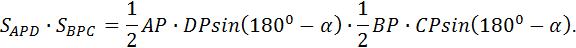
Здесь правые части равны, а поэтому и левые части равны.
10.4. Ведущий и каждый из 30 игроков записывают числа от 1 до 30 в некотором порядке. Затем записи сравнивают. Если у игрока и ведущего на одном и том же месте располагаются одинаковые числа, то игрок получает одно очко. Оказалось, что все игроки набрали различные количества очков. Докажите, что чья-то запись совпала с записью ведущего.
♦ Допустим первый игрок набрал 0 баллов, второй 1, третий 2, …, двадцать девятый 28. Тогда тридцатый набрал 30 баллов, т. е. его запись совпала с записью ведущего. Другие варианты приводят к этому ещё быстрее.
10.5. Найдите непрерывную функцию 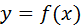 такую, что
такую, что  для всех
для всех 
♦ 
Ответ.  где
где  постоянная величина.
постоянная величина.
11.1. Про целые числа  и
и  известно, что
известно, что  Каково наименьшее возможное значение
Каково наименьшее возможное значение 
♦ Из равенства  следует, что
следует, что  делится на 5, поэтому
делится на 5, поэтому  делится на
делится на  , отсюда
, отсюда  делится на
делится на  . Из этого же равенства следует, что
. Из этого же равенства следует, что  делится на 2, поэтому
делится на 2, поэтому 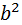 делится на 4, а значит,
делится на 4, а значит,  делится на 2, соответственно,
делится на 2, соответственно,  делится на
делится на  , т. е.
, т. е.  делится на
делится на 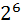 . Отсюда,
. Отсюда,  делится на
делится на  .. Ответ. 200000 =
.. Ответ. 200000 =  .
.
11.2. Решите уравнение 
♦ Ясно, что  Все выражения в скобках суммы
Все выражения в скобках суммы  принимают только неположительные значения, поэтому уравнение равносильно системе
принимают только неположительные значения, поэтому уравнение равносильно системе 

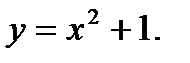 Отсюда,
Отсюда, 
Ответ. (0; 1).
11.3. Пусть  – точка из этой же плоскости, взятая вне квадрата. Наименьший угол с вершиной
– точка из этой же плоскости, взятая вне квадрата. Наименьший угол с вершиной  , содержащий в себе квадрат, является углом, под которым квадрат виден из точки
, содержащий в себе квадрат, является углом, под которым квадрат виден из точки  . Найдите геометрическое место точек плоскости, из которых данный в этой плоскости квадрат виден под прямым углом.
. Найдите геометрическое место точек плоскости, из которых данный в этой плоскости квадрат виден под прямым углом.
♦ Ответ. 4 полуокружности.
11.4. Все диагонали параллелепипеда равны. Докажите, что он прямоугольный.
♦Воспользоваться тем, что если диагонали параллелограмма равны, то он – прямоугольник.
11.5. Найдите все значения параметра  , при каждом из которых система имеет единственное решение
, при каждом из которых система имеет единственное решение
 .
.
♦ Если  решение системы при
решение системы при  , то
, то  тоже решение. Решение единственное при
тоже решение. Решение единственное при  А при
А при  система приобретает вид
система приобретает вид 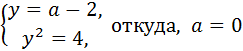 или
или  При
При  система
система  При
При  система
система  имеет решение (0; 2). Действительно, при
имеет решение (0; 2). Действительно, при  из первого уравнения
из первого уравнения  , а из второго
, а из второго  , противоречие,
, противоречие,
т. е. решений, в которых  , нет
, нет
Ответ. Система имеет единственное решение при 






