Владивосток, 9 ноября 2013 г., 11 класс
Победитель: Шибаев Иннокентий, МБОУ «Гимназия 1»
Призёры: Прохоров Дмитрий, МБОУ СОШ № 81,
Шевченко Александр, МБОУ СОШ № 23
Участников 74: решили задачу 1 – 1; задачу 2 – 7; задачу 3 – 6; задачу 4 – 5; задачу 5 – 2.
1. Для последовательностей  и
и  докажите, что
докажите, что 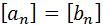 , где
, где 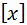 – целая часть
– целая часть  ;
; 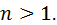
2. Решите уравнение 
3. Пусть  – точка из этой же плоскости, взятая вне квадрата. Наименьший угол с вершиной
– точка из этой же плоскости, взятая вне квадрата. Наименьший угол с вершиной  , содержащий в себе квадрат, является углом, под которым квадрат виден из точки
, содержащий в себе квадрат, является углом, под которым квадрат виден из точки  .Найдите геометрическое место точек плоскости, из которых данный в этой плоскости квадрат виден под углом
.Найдите геометрическое место точек плоскости, из которых данный в этой плоскости квадрат виден под углом  .
.
4. В доме 123 жильца, им вместе 3813 лет. Можно ли выбрать 100 из них, которым вместе не менее 3100 лет?
5. В тетраэдре (не обязательно правильном) два противоположных ребра перпендикулярны друг другу и имеют одну и ту же длину  . Кроме того, каждое из них перпендикулярно отрезку длины
. Кроме того, каждое из них перпендикулярно отрезку длины  , которое соединяет их середины. Найдите объём тетраэдра.
, которое соединяет их середины. Найдите объём тетраэдра.
Решения задач Владивостокской городской олимпиады
По математике 2013 г.
8.1. В последовательности 1; 1; 2; 3; 5; 8; 13; 21; … каждое следующее число равно сумме двух предыдущих. Могут ли в ней оказаться рядом два числа, делящихся на 13?
♦Нет. Тогда все предыдущие должны делиться на 13. А это не так.
8.2. Обыкновенная дробь  называется сократимой, если её можно сократить, то есть нацело разделить числитель и знаменатель на одно и то же целое число, больше 1. При каких
называется сократимой, если её можно сократить, то есть нацело разделить числитель и знаменатель на одно и то же целое число, больше 1. При каких 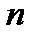 и на что можно сократить дробь
и на что можно сократить дробь 
♦ Предположим дробь сократима на натуральное число 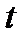 . Тогда
. Тогда 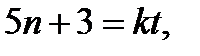
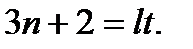 Откуда
Откуда 
 делитель числа 1,
делитель числа 1,  или 1.
или 1.
Ответ. Дробь несократима
8.3. Найдите  , если
, если  .
.
♦ Преобразуем уравнение  .Применим замену
.Применим замену  , и заметим, что
, и заметим, что  . Полученное в результате замены уравнение
. Полученное в результате замены уравнение  приведём к виду
приведём к виду  . Очевидные действия:
. Очевидные действия:
 ;
;
 ;
;  ;
;
 или
или  Ответ.
Ответ. 
Докажем, что  Для положительных
Для положительных  очевидно, что
очевидно, что  ; откуда
; откуда 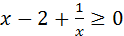 и
и  Тогда
Тогда  , для отрицательных
, для отрицательных  имеем
имеем  . Поэтому
. Поэтому 
♦ Другое решение. Выполнив умножение в левой части уравнения 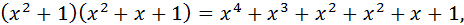 приведём уравнение к виду
приведём уравнение к виду  или
или  тогда
тогда 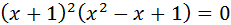 и
и  ,
,  . Мы воспользовались тем, что
. Мы воспользовались тем, что 
8.4. На стороне  треугольника
треугольника  взята точка
взята точка  , а на стороне
, а на стороне  точка
точка  . Отрезки
. Отрезки  и
и  пересекаются в точке
пересекаются в точке  Оказалось, что
Оказалось, что  и
и  . Докажите, что треугольник
. Докажите, что треугольник  равнобедренный.
равнобедренный.
♦ Треугольник  равнобедренный, поэтому
равнобедренный, поэтому 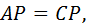 тогда
тогда  и
и 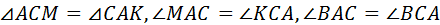 . Треугольник
. Треугольник  равнобедренный.
равнобедренный.
8.5. В пакете 256 леденцов. Двое играющих поочерёдно берут себе из пакета любое число леденцов, соблюдая два правила: правило вежливости – нельзя брать леденцов больше, чем взял противник, и правило честности – первым ходом нельзя брать все леденцы сразу. Победителем считается взявший последний леденец. Кто выиграет при правильной игре: начинающий или его партнёр?
♦ Если в пакете 2 леденца, то первый берёт один; второй тоже берёт один и побеждает. Если в пакете 4 леденца, и первый взял один леденец, то дальше по очереди они могут брать только по одному леденцу, и выигрыш у второго. Если первый взял два или три леденца, то второй забирает остальные и побеждает. После разбора случая восьми леденцов, а при необходимости 16 и т. д., становится ясно, что если первый возьмёт половину или больше леденцов, то проиграет; если игрок оставит нечётное число леденцов, то проиграет… Ответ. Выигрывает партнёр начинающего.
9.1. Числа  образуют арифметическую прогрессию, если существует число
образуют арифметическую прогрессию, если существует число  для которого
для которого 

 , … Числа
, … Числа  образуют геометрическую прогрессию, если существует число
образуют геометрическую прогрессию, если существует число  для которого
для которого 

 , … Три числа являются членами арифметической прогрессии. Три других числе являются членами геометрической прогрессии. Складывая соответствующие члены двух прогрессий последовательно, получили числа 85; 76 и 84 соответственно. Сумма всех членов арифметической прогрессии равна 126. Найдите эти прогрессии.
, … Три числа являются членами арифметической прогрессии. Три других числе являются членами геометрической прогрессии. Складывая соответствующие члены двух прогрессий последовательно, получили числа 85; 76 и 84 соответственно. Сумма всех членов арифметической прогрессии равна 126. Найдите эти прогрессии.
♦ Ответ. 68; 42; 16 и 17, 34; 68; 17; 42; 67 и 68; 34; 17.
Если арифметическую прогрессию образуют числа  , а геометрическую числа
, а геометрическую числа 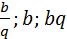 , то
, то 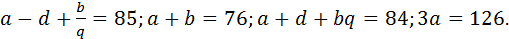 Осталось решить систему.
Осталось решить систему.
9.2. Известно, что  Найдите все аналогичные представления числа 5757 (т. е. 5757 =
Найдите все аналогичные представления числа 5757 (т. е. 5757 =  для целых
для целых  и
и  Докажите, что других нет.
Докажите, что других нет.
♦ Ответ.  Других нет. Предположим, что 5757 =
Других нет. Предположим, что 5757 =  ,
,  и
и  . Если оба числа
. Если оба числа  и
и 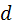 делятся на 3, то
делятся на 3, то  делится на 9, а 5757 делится на 3, но на 9 не делится. Противоречие. Если оба числа
делится на 9, а 5757 делится на 3, но на 9 не делится. Противоречие. Если оба числа  и
и 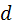 чётны или нечётны, то
чётны или нечётны, то  чётно, а 5757 нечётно. Противоречие. Если одно делится на 3, а другое нет, то вновь – противоречие: слева число не делится на 3, а справа делится. Эти рассуждения удобнее проводить, рассматривая остатки от деления чисел
чётно, а 5757 нечётно. Противоречие. Если одно делится на 3, а другое нет, то вновь – противоречие: слева число не делится на 3, а справа делится. Эти рассуждения удобнее проводить, рассматривая остатки от деления чисел  и
и 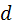 на 6. В силу равноправия чисел
на 6. В силу равноправия чисел  и
и 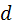 из симметричных вариантов можно рассматривать только один.
из симметричных вариантов можно рассматривать только один.
Остаток
от деления
 на 6 на 6
| Остаток
от деления
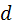 на 6 на 6
|
5757 = 
|
| 0 | 0 | Оба чётны. Невозможно. |
| 0 | 1 | Первое делится на 3, а второе нет. Невозможно. |
| 0 | 2 | Оба чётны. Невозможно. |
| 0 | 3 | Оба делятся е\на 3. Невозможно. |
| 0 | 4 | Оба чётны. Невозможно. |
| 0 | 5 | Первое делится на 3, а второе нет. Невозможно. |
| 1 | 1 | Оба нечётны. Невозможно. |
| 1 | 2 | 
|
| 1 | 3 | Второе делится на 3, а первое нет. Невозможно. |
| 1 | 4 |  все другие суммы больше 5757 все другие суммы больше 5757
|
| 1 | 5 | Оба нечётны. Невозможно. |
| 2 | 2 | Оба чётны. Невозможно. |
| 2 | 3 | Второе делится на 3, а первое не. Невозможно. |
| 2 | 4 | Оба чётны. Невозможно. |
| 2 | 5 | 
|
| 3 | 3 | Оба делятся на 3. Невозможно. |
| 3 | 4 | Первое делится на 3, а второе нет. Невозможно. |
| 3 | 5 | Первое делится на 3, а второе нет. Невозможно. |
| 4 | 4 | Оба чётны. Невозможно. |
| 4 | 5 | 
|
| 5 | 5 | Оба нечётны. Невозможно. |
9.3. Земной шар обвязали по экватору верёвкой. Затем верёвку удлинили на метр и приподняли над экватором так, что образовалась щель постоянной ширины. Сможет ли в эту щель пролезть кошка?
♦ Ширина щели  см для кошки не проблема.
см для кошки не проблема.
9.4. Решите в целых числах

♦ Ответ. (2; –1;–1;–-1), (–2; 1; 1; 1), (–1; 2;–1;–-1), (1; –2; 1; 1), (–1; –1; 2;–1), (1; 1; –2; 1),
(–1; –1;–1; 2), (1; 1; 1; –2). После вычитания из первого второе уравнение, получим  Отсюда,
Отсюда,  или
или  . Аналогично получим
. Аналогично получим  или
или  ; а также
; а также  или
или  . Рассмотрим один из восьми возможных случаев
. Рассмотрим один из восьми возможных случаев  . Тогда система сводится к одному уравнению
. Тогда система сводится к одному уравнению  . Из того, что
. Из того, что 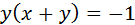 следует
следует  или
или 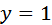 ..Если
..Если  , то
, то  . Если
. Если 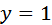 , то
, то  . Получили первое и второе целочисленныерешения системы.
. Получили первое и второе целочисленныерешения системы.
9.5. Диагонали разрезают четырёхугольник на четыре треугольника. Докажите, что четырёхугольник является параллелограммом тогда и только тогда, когда все четыре треугольника равновелики (т. е. все их площади равны).
♦ 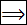 Площади любых смежных треугольников равны, так как у них основания равны, высота общая. Остальное очевидно.
Площади любых смежных треугольников равны, так как у них основания равны, высота общая. Остальное очевидно.
 Диагонали разбивают четырёхугольник
Диагонали разбивают четырёхугольник  на 4 равновеликих треугольника; Пусть
на 4 равновеликих треугольника; Пусть 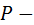 точка пересечения диагоналей четырёхугольника
точка пересечения диагоналей четырёхугольника  Пусть
Пусть  Тогда
Тогда  так как
так как  Площади треугольников равны, основание общее, поэтому у них высоты равны. Это означает, что
Площади треугольников равны, основание общее, поэтому у них высоты равны. Это означает, что  . Аналогично доказывается, что
. Аналогично доказывается, что  Стороны четырёхугольника попарно параллельны, значит, это – параллелограмм.
Стороны четырёхугольника попарно параллельны, значит, это – параллелограмм.
10.1. Числа  и числа
и числа  образуют арифметические програссии. При этом
образуют арифметические програссии. При этом  . Чему равно
. Чему равно 
♦ Пусть 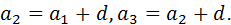 Характеристическое свойство арифметической прогрессии можно записать так
Характеристическое свойство арифметической прогрессии можно записать так  для первой прогрессии и так
для первой прогрессии и так  для второй.
для второй.

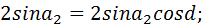
 или
или  .
.
Если  , то
, то  , что противоречит условию. Поэтому
, что противоречит условию. Поэтому  . Ответ.
. Ответ. 
10.2. Докажите, что нулевое решение (0; 0; 0) является единственным целочисленным решением уравнения 
♦ Если в решении одно из чисел 0, то и остальные два числа нули.. Пусть  k
k  – наибольшая степень двойки, которая делит
– наибольшая степень двойки, которая делит  и
и  ненулевого решения
ненулевого решения  тогда
тогда  . В левой части полученного уравнения все три слагаемых не могут быть чётными одновременно, так как по крайней мере одно из чисел
. В левой части полученного уравнения все три слагаемых не могут быть чётными одновременно, так как по крайней мере одно из чисел  и
и  нечётно. Не могут они быть все нечётными одновременно, так тогда слева число нечётное, а справа чётное. По этой же причине не может быть только одно нечётное. Если же предположим, что среди них ровно два нечётных, то окажется, что левая часть при делении на 4 даёт в остатке 2, а правая 0. Противоречие. Поэтому других решений, кроме нулевого, нет.
нечётно. Не могут они быть все нечётными одновременно, так тогда слева число нечётное, а справа чётное. По этой же причине не может быть только одно нечётное. Если же предположим, что среди них ровно два нечётных, то окажется, что левая часть при делении на 4 даёт в остатке 2, а правая 0. Противоречие. Поэтому других решений, кроме нулевого, нет.
10.3. Точки  и
и  лежат, соответственно, на сторонах
лежат, соответственно, на сторонах  и
и  квадрата
квадрата  . При этом
. При этом 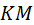 и
и  параллельны, а углы
параллельны, а углы  и
и 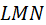 прямые. Докажите, что центр квадрата делит отрезок
прямые. Докажите, что центр квадрата делит отрезок  пополам.
пополам.
♦ Пусть 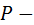 середина отрезка
середина отрезка  По теореме Фалеса она лежит на средней линии квадрата, параллельной сторонам
По теореме Фалеса она лежит на средней линии квадрата, параллельной сторонам  и
и  В прямоугольном треугольнике медиана, проведённая из вершины прямого угла, равна половине гипотенузы, поэтому
В прямоугольном треугольнике медиана, проведённая из вершины прямого угла, равна половине гипотенузы, поэтому  . Точка
. Точка  равноудалена от концовотрезка
равноудалена от концовотрезка 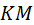 и поэтому лежит на серединном перпендикуляре отрезка
и поэтому лежит на серединном перпендикуляре отрезка 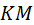 , т. е. на второй средней линии квадрата. Точка
, т. е. на второй средней линии квадрата. Точка  оказалась точкой пересечения средних линий квадрата, центром квадрата.
оказалась точкой пересечения средних линий квадрата, центром квадрата.
10.4. Существует ли 19 последовательных натуральных чисел, сумма которых делится на 87?
♦ Ответ. Да. Просуммируем равенства
87 = 87,
86 + 88 =  ,
,
85 + 89 =  ,
,
… … …
78 + 96 =  .
.
Получим слева сумму 19 последовательных целых чисел от 78 до 96, а справа число, кратное 87.
10.5.Известно, что 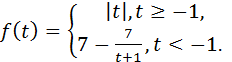 Решите уравнение
Решите уравнение 
♦ Так как  при
при  , то
, то  для всех
для всех  поэтому
поэтому  Уравнение равносильно такому
Уравнение равносильно такому  Если
Если  , то
, то  и
и  поэтому
поэтому 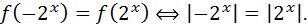 Последнее выполняется всегда, поэтому в ответ идут все числа
Последнее выполняется всегда, поэтому в ответ идут все числа  . Если
. Если  , то
, то  и
и  поэтому
поэтому  Ответ.
Ответ. 
11.1. Для последовательностей  и
и  докажите, что
докажите, что 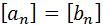 , где
, где 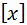 – целая часть
– целая часть  ;
; 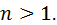
♦Заметим, что  не целое, так как
не целое, так как  , либо
, либо  не является полным квадратом.Также
не является полным квадратом.Также  – не целое, так как
– не целое, так как  не делится на 4.Доказательство проведём от противного. Пусть
не делится на 4.Доказательство проведём от противного. Пусть 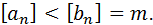 Тогда
Тогда
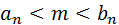 ;
; 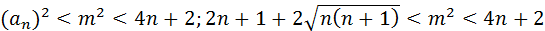

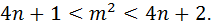 А такого быть не может. Поэтому
А такого быть не может. Поэтому 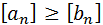 ,
,
Пусть  Тогда
Тогда 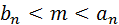 ;
; 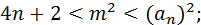



Такого тоже быть не может. Поэтому  ,
, 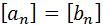 .
.
11.2. Решите уравнение 
♦  Преобразуем уравнение:
Преобразуем уравнение:  Здесь
Здесь 
 Поэтому уравнение равносильно системе
Поэтому уравнение равносильно системе
 Ответ. (0; 1).
Ответ. (0; 1).
11.3. Пусть  – точка из этой же плоскости, взятая вне квадрата. Наименьший угол с вершиной
– точка из этой же плоскости, взятая вне квадрата. Наименьший угол с вершиной  , содержащий в себе квадрат, является углом, под которым квадрат виден из точки
, содержащий в себе квадрат, является углом, под которым квадрат виден из точки  . Найдите геометрическое место точек плоскости, из которых данный в этой плоскости квадрат виден под углом
. Найдите геометрическое место точек плоскости, из которых данный в этой плоскости квадрат виден под углом  .
.
♦ Ответ 8 четвертинок окружности.
11.4. В доме 123 жильца, им вместе 3813 лет. Можно ли выбрать 100 из них, которым вместе не менее 3100 лет?
♦ Ответ. Да. Расположим жильцов в порядке возрастания возрастов. Возьмём сто самых старших и предположим им вместе меньше 3100 лет. Тогда возраст самого молодого из них меньше 31 года, а сумма всех 123 жильцов меньше, чем  Противоречие. Значит, сумма возрастов ста самых старших жильцов не меньше 3100 лет.
Противоречие. Значит, сумма возрастов ста самых старших жильцов не меньше 3100 лет.
11.5. В тетраэдре (не обязательно правильном) два противоположных ребра перпендикулярны друг другу и имеют одну и ту же длину  . Кроме того, каждое из них перпендикулярно отрезку длины
. Кроме того, каждое из них перпендикулярно отрезку длины  , которое соединяет их середины. Найдите объём тетраэдра.
, которое соединяет их середины. Найдите объём тетраэдра.
♦. Сечение, проходящее через ребро длины  и перпендикулярный ему отрезок длины
и перпендикулярный ему отрезок длины  разбивает тетраэдр на два тетраэдра, у каждого из которых высота равна
разбивает тетраэдр на два тетраэдра, у каждого из которых высота равна  , а в основании лежит треугольник площади
, а в основании лежит треугольник площади  Ответ.
Ответ. 






