МУНИЦИПАЛЬНЫЙ ЭТАП ВСЕРОССИЙСКОЙ ОЛИМПИАДЫ ПО МАТЕМАТИКЕ
Владивосток, 30 ноября 2013 г., 8 класс
Победитель: Сергеева Анастасия, Гуманитарно-экономический колледж ДВФУ
Призёр: Иванов Егор, МБОУ СОШ № 13
Участников 66: решили задачу 1 – 7; задачу 2 – 0; задачу 3 – 7; задачу 4 – 42; задачу 5 – 0.
1. В последовательности 1; 1; 2; 3; 5; 8; 13; 21; … каждое следующее число равно сумме двух предыдущих. Могут ли в ней оказаться рядом два числа, делящихся на 13?
2. Обыкновенная дробь 
называется сократимой, если её можно сократить, то есть нацело разделить числитель и знаменатель на одно и то же целое число, больше 1. При каких 
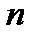и на что можно сократить дробь 
3. Найдите 
, если 
.
4. На стороне 
треугольника 
взята точка 
, а на стороне 
точка 
. Отрезки 
и 
пересекаются в точке 
Оказалось, что 
и 
. Докажите, что треугольник равнобедренный.
5. В пакете 256 леденцов. Двое играющих поочерёдно берут себе из пакеталюбое число леденцов, соблюдая два правила: правило вежливости – нельзя брать леденцов больше, чем только что взял противник, и правило честности – самым первым ходом в игре нельзя брать все леденцы сразу. Победителем считается взявший последний леденец. Кто выиграет при правильной игре: начинающий или его партнёр?
МУНИЦИПАЛЬНЫЙ ЭТАП ВСЕРОССИЙСКОЙ ОЛИМПИАДЫ ПО МАТЕМАТИКЕ
Владивосток, 23 ноября 2013 г., 9 класс
Победитель: Вознов Пётр, лицей «Технический»
Призёры: Шлык Иван, МБОУ СОШ № 23
Зикрицкий Гордей, МБОУ СОШ № 23
Участников 117: решили задачу 1 – 6; задачу 2 – 43; задачу 3 – 12; задачу 4 – 1: задачу 5 – 3.
1. Числа 
образуют арифметическую прогрессию, если существует число 
для которого 
, … Числа 
образуют геометрическую прогрессию, если существует число 
для которого 
, … Три числа являются членами арифметической прогрессии. Три других числе являются членами геометрической прогрессии. Складывая соответствующие члены двух прогрессий последовательно, получили числа 85; 76 и 84 соответственно. Сумма всех членов арифметической прогрессии равна 126. Найдите эти прогрессии.
2. Известно, что 
Найдите все аналогичные разложения числа 5757 (т. е. 5757 = 
для целых 
и 
и докажите, что других нет.
3. Земной шар обвязали по экватору верёвкой. Затем верёвку удлинили на метр и приподняли над экватором так, что образовалась щель постоянной ширины. Сможет ли в эту щель пролезть кошка?
4. Решите в целых числах
5. Диагонали разрезают четырёхугольник на четыре треугольника. Докажите, что четырёхугольник является параллелограммом тогда и только тогда, когда все четыре треугольника равновелики (т. е. все их площади равны).
МУНИЦИПАЛЬНЫЙ ЭТАП ВСЕРОССИЙСКОЙ ОЛИМПИАДЫ ПО МАТЕМАТИКЕ
Владивосток, 16 ноября 2013 г., 10 класс
Победитель: Понамарёва Ирина, МБОУ «Гимназия 1»
Призёр: Овчинников Максим, МБОУ СОШ № 23
Участников 86: решили задачу 1 – 1; задачу 2 – 0, задачу 3 – 2, задачу 4 – 23: задачу 5 – 5.
1. Числа 
и числа 
образуют арифметические прогрессии. При этом 
. Чему равно 
2. Докажите, что нулевое решение (0; 0; 0) является единственным целочисленным решением уравнения 
3.Точки 
и 
лежат, соответственно, на сторонах 
и 
квадрата 
. При этом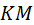 
и параллельны, а углы 
и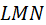 
прямые. Докажите, что центр квадрата делит отрезок 
пополам.
4. Существует ли 19 последовательных натуральных чисел, сумма которых делится на 87?
5. Известно, что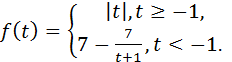 
Решите уравнение 
