Существуют и другие непараметрические кригерии, позволяющие проверять гипотезы с минимальным количеством расчетов.
Критерий рангов позволяет проверить, является ли порядок следования каких-либо событий или результатов случайным, или же он связан с действием какого-то фактора, не учтенного исследователем. С помощью этого критерия можно, например, определить, случаен ли порядок чередования мужчин и женщин в очереди В нашем опыте этот критерий позволил бы узнать, не чередуются ли плохие и хорошие резульгаты каждого испытуемого опытной группы после воздействия каким-то определенным образом или не приходятся ли хорошие результаты в основном на начало или конец испытаний.
При работе с этим критерием сначала выделяют такие последовательности, в которых подряд следуют значения меньше медианы, и такие, в которых подряд идут значения больше медианы. Далее по таблице распределения R (от англ. runs- последовательности) проверяют, обусловлены ли эти различные последовательности только случайностью.
При работе с порядковыми данными1 используют такие непараметрические тесты, как тест U (Манна-Уитни) и тест Т Вилкоксона. Тест U позволяет проверить, существует ли достоверная разница между двумя независимыми выборками после того, как сгруппированные данные этих выборок классифицируются и ранжируются и вычисляется сумма рангов для каждой выборки. Что же касается критерия Т, то он используется для зависимых выборок и основан как на ранжировании, так и на знаке различий между каждой парой данных.
Чтобы показать применение этих критериев на примерах, потребовалось бы слишком много места. При желании читатель может подробнее ознакомиться с ними по специальным пособиям.
1 Такие данные чаще всего получаются при ранжировании количественных данных, которые нельзя обработать с помощью параметрических тестов
Статистика и обработка данных 307
Корреляционный анализ
При изучении корреляций стараются установить, существует ли какая-то связь между двумя показателями в одной выборке (например, между ростом и весом детей или между уровнем IQ и школьной успеваемостью) либо между двумя различными выборками (например, при сравнении пар близнецов), и если эта связь существует, то сопровождается ли увеличение одного показателя возрастанием (положительная корреляция) или уменьшением (отрицательная корреляция) другого.
Иными словами, корреляционный анализ помогает установить, можно ли предсказывать возможные значения одного показателя, зная величину другого.
До сих пор при анализе результатов нашего опыта по изучению действия марихуаны мы сознательно игнорировали такой показатель, как время реакции. Между тем было бы интересно проверить, существует ли" связь между эффективностью реакций и их быстротой. Это позволило бы, например, утверждать, что чем человек медлительнее, тем точнее и эффективнее будут его действия и наоборот.
С этой целью можно использовать два разных способа: параметрический метод расчета коэффициента Браве - Пирсона (г) и вычисление коэффициента корреляции рангов Спирмена (г,), который применяется к порядковым данным, т. е. является непараметрическим. Однако разберемся сначала в том, что такое коэффициент корреляции.
Коэффициент корреляции
Коэффициент корреляции - это величина, которая может варьировать в пределах от +1 до — 1. В случае полной положительной корреляции этот коэффициент равен плюс 1, а при полной отрицательной - минус 1. На графике этому соответствует прямая линия, проходящая через точки пересечения значений каждой пары данных:
. Переменная 8
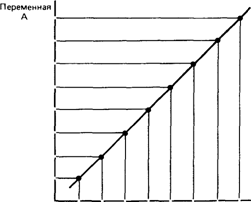
Полная положительная корреляция (г =+1)
308 Приложение Б
\
Переменная В
| Переменная А | \ | |||||||
| ) К | ||||||||
| ^ | ||||||||
| \ | ||||||||
| \ | ||||||||
| ^ | ||||||||
| \ | ||||||||
| \ | ||||||||
Полная отрицательная корреляция (/" ^-l)
В случае же если эти точки не выстраиваются по прямой линии, а образуют «облако», коэффициент корреляции по абсолютной величине становится меньше единицы и по мере округления этого облака приближается к нулю:
' -0,30 r=0
В случае если коэффициент корреляции равен 0, обе переменные полностью независимы друг от друга.
В гуманитарных науках корреляция считается сильной, если ее коэффициент выше 0,60; если же он превышает 0,90, то корреляция считается очень сильной. Однако для того, чтобы можно было делать выводы о связях между переменными, большое значение имеет объем выборки: чем выборка больше, тем достовернее величина полученного коэффициента корреляции. Существуют таблицы с критическими значениями коэффициента корреляции Браве - Пирсона и Спирмена для разного числа степеней свободы (оно равно числу пар за вычетом 2, т. е. п — 2). Лишь в том случае, если коэффициенты корреляции больше этих критических значений, они могут считаться достоверными. Так, для того чтобы коэффициент корреляции 0,70 был достоверным, в анализ должно быть взято не меньше 8 пар данных (г| = п — 2 = 6) при вычислении г (табл. В.4) и 7 пар данных (г| = и — 2 = 5) при вычислении г, (табл. 5 в дополнении 6.5). - ——-
309
Статистика и обработка данных






