Чтобы повысить надежность объекта применяется резервирование. Резервирование – это способ обеспечения надежности за счет использования дополнительных средств и (или) возможностей, избыточных по отношению к минимально необходимым для выполнения требуемых функций.
Основным параметром резервирования является его кратность. Под кратностью резервирования понимается отношение числа резервных изделий (элементов) к числу основных, выраженное несокращенной дробью.
Резервирование с целой кратностью называется такое резервирование, при котором для нормальной работы резервированного соединения достаточно, чтобы исправным был хотя бы один элемент расчета.
При резервировании с дробной кратностью нормальная работа резервированного соединения возможна при условии, что число исправных элементов не менее необходимого для нормальной работы.
В условиях задачи 2 принято, что все элементы установки равнонадежны и для них справедлив экспоненциальный закон надежности, поэтому вероятность безотказной работы в течение времени t любого элемента равна
Р(t)=ехр (-lэ t), (2.1)
где lэ- интенсивность отказов одного любого элемента.
Установка состоит из четырех узлов. Для повышения надежности устройства каждый узел резервирован различными способами, т.е. в схеме наряду с основными элементами, необходимыми для выполнения функциональных задач устройства, присоединены резервные элементы. В результате этого отказ узла, а, следовательно, и всего устройства, возможен только при отказе основного и резервного элемента.
В узле «а» применено общее резервирование с постоянным включением резерва и с целой кратностью.
Вероятность безотказной работы в этом случае вычисляется по формуле
Р а(t)=1-[1-ехр (-li t)]m+1, (2.2)
где li =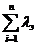 
- интенсивность отказов всех элементов основной или резервной цепи; m – число резервных цепей (кратность резервирования); n - число элементов основной и резервной цепи.
В узле «б» применено раздельное резервирование с постоянно включенным резервом и с целой кратностью. Вероятность безотказной работы в этом случае вычисляется по формуле
Р б(t)={1-[1-ехр (-lэ t)]m+1}n, (2.3)
где n- число последовательно соединенных групп элементов.
В узле «в» применено общее резервирование замещением с целой кратностью и ненагруженном состоянии резерва. Вероятность безотказной работы в этом случае вычисляется по формуле
Рв(t)=ехр (-li t) 
, (2.4)
где li = 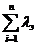- интенсивность отказов всех элементов основной цепи; m – число резервных цепей (кратность резервирования); n- число элементов основной цепи.
В узле «г» применено общее резервирование с дробной кратностью и постоянно включенным резервом. Число элементов, необходимых для нормальной работы в этом узле равно k= 2. Вероятность безотказной работы в этом случае вычисляется по формуле
Р г(t) = 
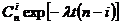
, (2.5)
где n- число элементов, l - интенсивность отказа одной цепи, т.е. lэ. Вероятность безотказной работы установки «А» равна произведению вероятностей безотказной работы всех узлов, т.е.
Р А(t)= Р а(t)· Р б(t)· Р в(t)· Р г(t). (2.6)
Вероятность безотказной работы для системы из двух параллельно включенных установок «А» и «Б» вычисляется по основной формуле для общего резервирования с постоянно включенным резервом и с целой кратностью для неравнонадежных установок
Р АБ = 1- 
=1-(1- Р А)(1- Р Б). (2.7)
где Р i –вероятность безотказной работы одной из установок, m - кратность резервирования.
Потребность в запасных частях определяется средним расходом элементов за определенный промежуток времени и заданной вероятностью Р z обеспечения запасными элементами, т.е. с какой вероятностью не будет простоев вследствие отсутствия запасных элементов для замены вышедших из строя.
При экспоненциальном распределении наработки до отказа среднее число отказавших элементов Z ср за период t определяется по формуле
Z ср= N lэ t, (2.8)
где N – число элементов, находящихся в эксплуатации;
lэ - интенсивность отказов одного элемента, 1/ч;
t – период работы, ч.
В соответствии с условиями задачи количество элементов всех установок, находящихся в эксплуатации в течение года, равно
N= с · С, (2.9)
где с - количество элементов одной установки; С - общее количество установок, находящихся в эксплуатации.
Чем выше заданное значение вероятности Р z, тем большим должен быть запас элементов. В инженерных расчетах норм запасных частей применяются упрощенные методы.
При Р z=0,95 число запасных элементов Z можно вычислить по приближенным формулам
z =5+1,12zср при 20< z ср£60..70; (2.10)
z =10+1,06 zср при z ср >60..70. (2.11)
При вычислении числа запасных элементов для других значениях Рz можно пользоваться табличными данными зависимости
Z = р · Z ср, (2.12) где р – коэффициент, определяемый в зависимости от заданного значения вероятности Р z и среднего значения числа отказавших элементов Z ср.
Таблица 8
Значения р = Z/Zср
| Р z | Z ср | |||||||
| 25 | 50 | 75 | 100 | 150 | 200 | 300 | 400 | |
| 0,900 | 1,24 | 1,18 | 1,15 | 1,12 | 1,10 | 1,09 | 1,07 | 1,06 |
| 0,920 | 1,27 | 1,20 | 1,16 | 1,14 | 1,11 | 1,10 | 1,08 | 1,07 |
| 0,940 | 1,30 | 1,22 | 1,17 | 1,15 | 1,13 | 1,11 | 1,09 | 1,08 |
| 0,960 | 1,35 | 1,25 | 1,20 | 1,17 | 1,14 | 1,12 | 1,10 | 1,09 |
| 0,980 | 1,41 | 1,30 | 1,24 | 1,21 | 1,17 | 1,15 | 1,12 | 1,10 |
| 0,990 | 1,47 | 1,34 | 1,27 | 1,23 | 1,19 | 1,17 | 1,13 | 1,12 |
| 0,996 | 1,55 | 1,38 | 1,31 | 1,27 | 1,22 | 1,19 | 1,15 | 1,13 |
| 0,999 | 1,66 | 1,46 | 1,37 | 1,32 | 1,26 | 1,22 | 1,18 | 1,15 |
