Надежностью называется свойство объекта (установки, системы, элемента) сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, хранения и транспортирования.
Для выполнения своих функций объект должен находиться в работоспособном состоянии. Работоспособное состояние – это состояние объекта, при котором значения всех параметров, характеризующих способность выполнять заданные функции, соответствуют требованиям нормативно- технической и (или) конструкторской (проектной) документации.
При расчете надежности функционирования невосстанавливаемых объектов интересуются продолжительность работы до первого отказа – наработки до отказа. Отказ – это событие, заключающееся в нарушении работоспособного состояния.
Интенсивность процессов возникновения отказов во времени принято обозначать l(t). Вероятность безотказной работы или функция надежности Р (t) выражает вероятность того, то невосстанавливаемый объект не откажет к моменту времени наработки t.
В задаче 1 рассматривается изделие, состоящее из большого числа элементов различного типа и имеющих разные показатели интенсивности отказов. Интенсивность отказов в рассматриваемый период времени величина постоянная для каждого элемента, т.е. для всех элементов справедлив экспоненциальный закон распределения наработки до отказа. Восстановление работоспособности элементов не предусмотрено. Надежность работы установки зависит от надежности работы отдельных элементов. Все элементы по признаку надежности соединены последовательно.
При экспоненциальном распределении наработки до отказа вероятность безотказной работы элемента с интенсивностью отказов l(t) = const в течение времени t однозначно определяется по формуле
Р (t)= ехр (-l t). (1.1)
Если все элементы n данного типа равнонадежны, т.е. имеет одинаковую интенсивность отказов lэ, то интенсивность отказов всех элементов данного типа lс равна сумме интенсивностей отказов элементов
lс = n lэ, (1.2)
а вероятность безотказной работы системы состоящей из одинаковых элементов в течение времени t определяется по формуле
Р с(t)= ехр (- n lэ t). (1.3)
Для изделия состоящего из N последовательно по признаку надежности соединенных систем из одинаковых элементов вероятность безотказной работы изделия подчиняется закону умножения надежностей и определяется по формуле
P и (t)=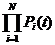 
, (1.4)
где Р i – вероятность безотказной работы системы элементов i - того типа.
Поскольку все элементы каждого типа равнозначны, то интенсивность отказов всего изделия можно определить по формулу
lи=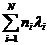 
, (1.5)
где n i - число элементов i -того типа; li - интенсивность отказов элементов i -того типа; N – число типов (систем) элементов.
Зная интенсивность отказов всего изделия lи вероятность безотказной работы изделия можно определить по формуле
Р и(t) = ехр (-lи t). (1.6)
Среднее время наработки до отказа изделия равно
То.ср. =1/lи. (1.7)
Таким образом, вычисление вероятности безотказной работы изделия можно выполнить, определяя последовательно вероятность безотказной работы всех отдельных систем по формуле (1.3), а затем всего изделия по формуле (1.4) или сначала определить интенсивность отказов всего изделия по формуле (1.5), а затем вероятность безотказной работы за время t по формуле (1.6).
