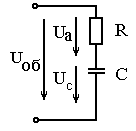Пример 4.5. Последовательное соединение резистора и конденсатора в цепи синусоидального тока.

К цепи с последовательным соединением активного сопротивления

 R = 12 Ом и емкостного Х_с = 16 Ом подведено общее напряжение u_об =170sinwt, В. Определить ток в цепи, активную, реактивную и полную мощности, построить векторную диаграмму.

 

Решение.

Полное сопротивление цепи .

По закону Ома находим ток в цепи:

 

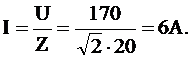
Символ квадратного кореня из двух появился в формуле чтобы перевести амплитудное значение напряжения в действующее.

 

Мощности, выделяющиеся в цепи:

активная Р = I² · R=36 · 12 = 432 Вт,

реактивная Q_С = I² · X_{C =} 6² · 16 = 576 Вар,

полная   S =UI = 120 · 6 = 720 ВА.

 

При построении диаграммы, прежде всего, строим вектор тока I, поскольку он одинаков для всех элементов последовательной цепи. Активное напряжение U_a совпадает по фазе с током, ёмкостное – U_С  отстаёт от тока на угол 90 градусов. (Учитывая, что вектора на диаграммах вращаются против часовой стрелки, направляем вектор напряжения U_С вниз.) Общее напряжение U_об равно векторной сумме напряжений U_a и U_С. Этот вектор проводится из начала вектора U_a в конец вектора U_С.

 

Пример 4.6.   Цепь с последовательным соединением резистора, индуктивности и конденсатора.

 

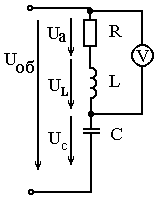Неразветвлённая цепь содержит последовательно включённые сопротивления: R=4 Ом, X_L = 7 Ом и X_C = 10 Ом. Напряжение на зажимах цепи U_об = 24 В. Определить ток, реактивную мощность цепи, напряжение на резисторе и на индуктивности, а также показания вольтметра. Построить векторную диаграмму.

Решение.

Полное сопротивление цепи

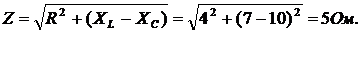
Ток в цепи, по закону Ома:

I = U/Z == 24/5 = 4,8 А.

 

Напряжение на резисторе:

U_R=IR=4,8 · 4=19,2 В.

 

Напряжение на индуктивности:

U_L=I · X_L=4,8 · 7=33,6 В.

 

Вольтметр подключён так, что показывает суммарное напряжение на R и L. Как известно, в цепях переменного тока нельзя складывать величины арифметически. В соответствии с векторной диаграммой для данной цепи, по теореме Пифагора:

U_{вольтметра}=

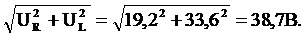
Построение векторной диаграммы начинается с вектора тока. Затем последовательно, в виде цепочки векторов, строятся вектора напряжений на элементах цепи: U_а, U_L, U_С, Uоб. Прежде всего, отображается вектор активного напряжения U_а, которое совпадает с током по фазе. Затем строится вектор напряжения  U_L, опережающий ток по фазе на 90 градусов. После этого откладывается вектор напряжения  U_С, который отстаёт по фазе от тока на 90 градусов.  Последним строится вектор общего напряжения Uоб. Его проводят от начала вектора  U_а к концу вектора U_С.

Общее напряжение U_об равно векторной сумме напряжений U_а, U_L и U_С.

Реактивная мощность: Q_С = I²(X_L-X_C) = 4,8²(7-10) = - 69,1 Вар. (Реактивная мощность получилась отрицательной, что указывает на то, что она имеет ёмкостный характер.)

Пример 4.7   Резонанс напряжений.

Цепь с последовательным соединением активного сопротивления R, индуктивности L и емкости C настроена на резонанс напряжений. При этом сопротивления элементов цепи: R = 3 Ом, X_L ,= Xc = 15 Ом. Напряжение на входе цепи U_об = 24 В. Определить ток в цепи, индуктивное напряжение U_L, активную мощность Р и реактивную мощность Q_об, выделяющуюся в цепи.

Решение.

Полное сопротивление цепи Z при резонансе напряжений равно активному R = 3 Ом, а ток в цепи 

I = U / z = 24/3 = 8 А.

Напряжение на индуктивности U_L =I · X_L= 8 · 15= 120 В. (Заметьте, что напряжение на реактивном элементе получилось много больше напряжения U_об на входе всей цепи.)

     

Активная мощность, выделяющаяся в цепи:

Р = UI = 24 • 8 = 192 Вт.

Реактивная мощность Q_об, выделяющаяся в цепи, равна нулю, т.к. при резонансе цепь ведёт себя как чисто активное сопротивление. (Реактивные мощности Q_L и Q_C, выделяющиеся в реактивных элементах цепи равны по величине и противоположны по знаку.) Следовательно, при резонансе общая мощность цепи S равна активной мощности Р.

Пример 4. 8. Расчёт простейшей разветвлённой цепи.

Общий ток I в неразветвленной части цепи переменного тока составляет 1 А при напряжении на зажимах цепи 60 В. Коэффициент мощности цепи cosφ=0,6.

Определить активную I_а и емкостную составляющие I_с тока, активное сопротивление, емкость конденсатора C, если частота тока f составляет 50 Гц. Построить векторную диаграмму для данной схемы.

Решение.

Построим векторную диаграмму для цепи. Построение начинаем с вектора напряжения U, поскольку оно является одинаковым для обеих ветвей цепи. Вектор тока в резисторе I_a совпадает по фазе с напряжением. К концу вектора     I_a пристраиваем вектор тока в конденсаторе I_с . Этот вектор направлен вниз, поскольку ток в конденсаторе отстаёт по фазе от напряжения на угол 90 градусов.

Вектор общего тока I_об проводим из начала первого в конец последнего вектора. Ток I_об является суммой токов в ветвях.

Зная коэффициент мощности цепии величину тока I_об, находим величину токов в ветвях:

I_a= I_об·cosj = 1· 0,6 = 0,6A;

I_a = I_об·sinj = 1· 0,8 = 0,8А.

Значение sinj найдено по значению cosj.

 

Теперь можно найти величину сопротивления:

R = U / I_a = 60 / 0,6 = 100 Ом.

X_c = U / I_c = 60 / 0,8 = 75 Ом.

Из формулы ёмкостного сопротивления X_c = 1 / 2p·f·C найдём величину ёмкости конденсатора:

С = 1 / 2p·f·X_c = 1 / 2·3,14·50·75 =0,0000425 Ф = 42,5 мкФ.

Пример 4. 9. Расчёт цепи переменного тока с параллельным соединением ветвей без использования метода проводимости.

Приборы, включенные в цепь переменного тока, показывают: амперметры (A1 и А2 ) — 10 А, вольтметр — 220 В, ваттметр — 3520 Вт. Определить ток всей цепи и угол сдвига фаз тока I относительно напряжения U.

Решение.

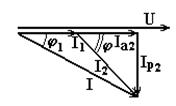Перед началом решения задачи проанализируем схему. В левой ветви схемы (в неё входит резистор R₁) протекает ток I₁ активного характера, т. к. в ветви включено только активное сопротивление. В правой ветви (она состоит из последовательно включённых элементов: резистора R₂ и индуктивности L) протекает ток I₂ активно-индуктивного характера. Величину токов в ветвях показывают амперметры.

Вольтметр показывает напряжение на входе цепи. Ваттметр показывает активную мощность, потребляемую всей цепью. Общий ток равен векторной сумме токов в ветвях.

На основании проведённого анализа построим векторную диаграмму для данной цепи. Сначала построим вектор напряжения на входе цепи U. Затем строим активный ток в левой ветви I₁ и активную составляющую тока в правой ветви I_a2, совпадающие по фазе с напряжением на входе цепи. Реактивная (индуктивная) составляющая тока I_p2 в правой ветви отстаёт по фазе от напряжения на угол 90 градусов. Общий ток равен сумме векторов I₁ + I_a2 + I_p2.

Активная составляющая тока всей цепи I_a слагается из двух составляющих I₁ + I_a2 = P/U = 3520 / 220 = 16 А.

Активная составляющая второго тока I_{a2_} = I_a - I₁ = 16 - 10 = 6 А. Реактивная составляющая второго тока I_p2=

Ток всей цепи

Пример 4. 10. Расчёт цепи переменного тока при параллельном соединении ветвей методом проводимости

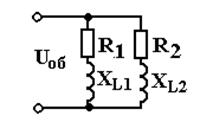    Две катушки индуктивности соединены параллельно и имеют сопротивления: r₁= 6 Ом,

 x_L1 = 8 Ом; r₂ = 8 Ом; x_L2 = 6 Ом. Напряжение источника энергии U = 220 В. 

Определить токи в ветвях, ток в неразветвленной части цепи и активную мощность Р. Построить диаграмму проводимостей.

Решение.

  Определим проводимости ветвей и общую проводимость всей цепи.

Активная проводимость левой ветви: g₁=r₁/z₁² =6/ (6² +8²) =6 ·10^-2 Cм.

Активная проводимость правой ветви: g₂=r₂/z₂² =8/(8² +6²) = 8·10^-2 Cм.

Реактивная проводимость левой ветви: b₁= x₁/z₁² =8/ (6² +8²) =8 ·10^-2 Cм

Реактивная проводимость правой ветви: b₂=x₂/z₂² =6/(8² +6²) = 6·10^-2 Cм.

Токи в ветвях: I₁=U·y₁=U · ;

                     I₂=U·y₂=220·10·10^-2=22A.

  Чтобы найти общий ток в неразветвлённой части цепи построим диаграмму проводимостей.

    Из рассмотрения диаграммы становится понятным принцип вычисления полной проводимости всей цепи по известным проводимостям ветвей. (В большом треугольнике горизонтальный катет равен сумме активных проводимостей, а вертикальный - сумме реактивных проводимостей. По теореме Пифагора находим гипотенузу треугольника, которая изображает полную проводимость всей цепи.)

Общая проводимость цепи:

Ток в неразветвлённой части цепи I =U·Y=220·19,7·10^-2 =43,3A.

Пример 4.11. Расчёт цепи с конденсатором с использованием метода комплексных чисел

К конденсатору С2, обладающему ёмкостным сопротивлением x_С2= 6 Ом, приложено напряжение U₂= 300e 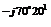В. Найти ток в цепи.

Решение:

Прежде всего выражаем сопротивление конденсатора в комплексной форме:

Z ₂= -j6 = 6e  Ом.

Затем, по закону Ома, находим ток в цепи:

I₂= U₂ / Z ₂ = 300e 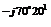/ 6e  = 50e А.

Пример 4.12. Расчёт последовательной цепи с использованием комплексных чисел.

К цепи с последовательным сопротивлением элементов r₃= 10 Ом и X_L3 = 8 Ом подключено напряжение U₃= 300e 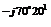В.

Найти ток в цепи и напряжение на каждом элементе.

Решение:

Сначала находим комплексное сопротивление цепи:

Z ₃= r₃+jx 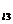= 10 + j8 = 12,8e  Ом.

Теперь можно найти ток в цепи по закону Ома:

I₃ = U₃ / Z ₃ = U₃= 300e 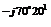/ 12,8e = 23,8  А.

Теперь найдем напряжение на резисторе

U_а = I_{3 *}r =23,8  _* 10 = 238 В

и на индуктивном сопротивлении

U_L = I_{3 *}X_L = 23,8 _* j8 = 190,4 В.

 

Задача 20

Определить показания вольтметра, если известны параметры цепи:                              Uобщ = 100 В, R = 30 Ом, Х_L = 90 Ом, Хс = 50 Ом.

    Постройте в масштабе векторную диаграмму для тока и напряжений.

Ответ: показания вольтметра 100В 

 

Задача 21*

    В электрической цепи протекает ток I = 5 A, частота приложенного к цепи напряжения f = 50 Гц. Напряжения на элементах цепи составляют: U₁ = 50 B, U₂ = 100 B, U₃ = 60 B.

Определите напряжения на элементах этой цепи, если, при том же напряжении U на входе цепи, частота возрастёт до 100 Гц?

    Постройте в масштабе векторную диаграмму для тока и напряжений при частоте 50 герц.

Ответ: U₁ =18В; U₂ =75В; U₃ =11,2В.

 

Задача 22

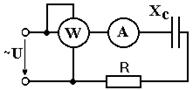    Определить величину активного сопротивления R, а также индуктивного сопротивления X_C, если ко входу цепи приложено напряжение U = 200 B, ваттметр показывает активную мощность 640 Вт,  а амперметр - ток 4 А. 

    Постройте в масштабе векторную диаграмму для тока и напряжений.

    Ответ: R= 40 Ом; X_С = 30 Ом

Задача 23

    Определить сопротивления резистора R и конденсатора X_C, если приборы в цепи показывают: мощность Р = 90 Вт, ток всей цепи I­₁ = 5 A, ток через конденсатор I₂ = 4 A.

    Постройте в масштабе векторную диаграмму для тока и напряжений.

 

Ответ: R = 10 Ом; X_C = 7,5 Ом.

 

 

Задача 24*

    К схеме приложено переменное напряжение, частотой f = 50 Гц. В схеме протекает ток I = 5 A.  При этом на резисторе действует напряжение U₁ = 50 B, на катушке индуктивности U₂ = 100 B, а на конденсаторе U₃ = 60 B.

Определите, при какой частоте приложенного напряжения в схеме возникнет резонанс напряжений.Каким будет ток в цепи, если величина входного напряжения не изменится?

Ответ: резонанс возникнет при частоте 40 Гц, ток в цепи при резонансе составит 6,4 А.

Задача 2 5

    Определить сопротивление R и активную мощность Р цепи, если X_L = 30 Ом, амперметр

показывает 4 А, вольтметр 200 В. 

    Постройте в масштабе векторную диаграмму для напряжения и токов.

 

Ответ: R = 40 Ом, Р = 640 Вт.

Задача 26*

Определите активную мощность цепи. Необходимые для расчёта данные возьмите с рисунка.

 

Ответ: 1. 1480 Вт.

 

Задача 27^*

    Определить напряжение U на входе цепи, общий ток цепи I, напряжение на горизонтальной ветви U₁, напряжение на индуктивности U₂, и напряжение U­_3, на цепочке, состоящей из элементов L и C.

Известно, что: X_L = X_C = R = 5 Ом, I₃ = 10 A.

 

Ответы:   I = 20 A; U₁ = 141B; U₂ = 50 B;

           U₃ = 0; U = 180 B.

Задача 28

Цепь переменного тока с последовательным соединением активного сопротивления, индуктивности и емкости настроена на резонанс напряжений. При этом активное сопротивление R = 3 Ом, индуктивное сопротивление X_L равно ёмкостному сопротивлению X_Си составляют 20 Ом каждое.

Напряжение на входе цепи U_об = 12 В. Определить ток в цепи и напряжение U_L на индуктивности. Найти активную и реактивную мощности, выделяющиеся в цепи.

Построить векторную диаграмму без масштаба. Определить величину индуктивности L и ёмкости С, если резонанс возник на частоте 250 Гц.

Задача 29

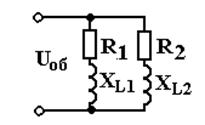Две катушки индуктивности соединены параллельно и имеют сопротивления: R₁= 6 Ом, X_L1 = 8 Ом; R₂ = 16 Ом; X_L2 = 12 Ом. Напряжение источника энергии U = 220 В.

Найти токи в ветвях и общий ток двумя разными способами: а) путём построения в масштабе векторной диаграммы; б) используя метод комплексных чисел.

Задача 30

К цепи с последовательным соединением активного сопротивления R = 12 Ом и индуктивности 314мГн подведено общее напряжение U =120 вольт. Определить действующее значение тока в цепи, активную, реактивную и полную мощности, построить векторную диаграмму без масштаба.

 

Задача 31

В сеть переменного тока с действующим напряжением 220 В включены последовательно конденсатор емкостью 100 мкФ, катушка индуктивностью 0,4 Гн и активное сопротивление 8 Ом. Определите амплитуду силы тока в цепи, если частота переменного тока 200 Гц. Найдите также частоту переменного тока, при которой в данной схеме наступит резонанс напряжений.

Ответы: ток в цепи при резонансе 0,43А; частота, при которой возникает резонанс 25 Гц.

        

5. Цепи трёхфазного тока

Решение задач на трехфазный ток требует знания свойств соединения потребителей звездой и треугольником, умения строить векторные диаграммы для указанного соединения.