Пример 2.5. Смешанное соединение резисторов

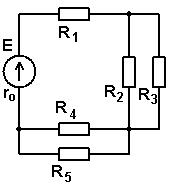
Для цепи, приведённой на рисунке, известна величина сопротивлений: R₁ = 10 Ом, R₂ = 15 Ом, R₃ = 25 Ом, R₄ = 50 Ом, R₅ = 5 Ом и ток I₁ == 2 А.

Определить токи I₃, I₄, I₅, протекающие в резисторахи напряжение U на зажимах цепи.

Решение

Прежде всего следует проанализировать схему и найти в ней резисторы, соединённые последовательно. В данном случае устанавливаем, что резисторы R₁ и R₂ соединены последовательно. В ходе решения их можно заменить одним сопротивлением R₁₂. В них протекает одинаковый ток

I₁ = I₂ =1А.

 

Зная ток, протекающий в резисторе R1, найдём (по закону Ома) напряжения на резисторах R₁ и R₂. 

U₁ = I₁ · R₂ = 2 · 10 = 20 В,

 U₂ = I₁ · R₂ = 2 · 15 = 30 В.

Найдем сумму этих напряжений:

U₁₂ = U₁+U₂ = 20+30 = 50 В.

 

Далее, анализируя схему, замечаем, что участки с сопротивлениями R₁+R₂, R₃ и R₄ соединены параллельно. При параллельном соединении напряжения на этих участках равны:

U₁₂ = U₃ = U₄ = 50 В.

Следовательно, токи в параллельных ветвях:

 I₃= U₃/R₃ = 50/25 = 2 А,

I₄= U₄/R₄  = 50/50 =1A.

 

По первому закону Кирхгофа ток, подтекающий к узлу А, равен сумме токов оттекающих от узла:

I₅=I₁+I₃+I₄ = 2+2+1 = 5 А.

Напряжение на резисторе R₅:

U₅ = I₅ · R₅ = 5 · 5 = 25B.

Общее напряжение на зажимах цепи:

U = U₁+U₃ = 25+50 == 75 В.

Пример 2.6. Расчёт цепи, содержащей источник ЭДС и смешанное соединение резисторов потребителя

Определить ЭДС источника, если его внутреннее сопротивление Ri =1,2 Ом, выделяемая в резисторе R2, мощность Р₂= 24 Вт. Сопротивления резисторов: R1 = 0,8 Ом, R2 = 6 Ом, R3 = 3 Ом, R4 = R5 = 0,8 Ом      (рис 1.1).

Чему равна полезная мощность, развиваемая в данной цепи источником и КПД (h) источника? Как изменится потребляемый ток, полезная мощность и КПД источника, если в резисторе R2 произойдет короткое замыкание?    

Решение.

Решение данной задачи слагается из фрагментов, рассмотренных в примерах 1.1 – 1.3. и в примерах 2.1 – 2.5

а) Для решения задачи следует найти эквивалентное сопротивление всех резисторов, подключенных к источнику ЭДС.

Резисторы R₂ и R₃, а также резисторы R₄ и R₅ соединены параллельно. Найдём общее сопротивление для каждой из этих групп:

R₂₃=R₂·R₃/(R₂+R₃₎= 6·3/(6+3)=2 Ом;

R₄₅=R₄·R₅/(R₄+R₅)= 0,4 Ом.

Общее сопротивление всех резисторов, подключённых к источнику ЭДС в качестве нагрузки

R_об= R₁+R₂₃+R₄₅=0,8+2+0,4=3,2 Ом.

 

б) Чтобы найти КПД источника нужно знать полезную и полную мощность, отдаваемую источником.

Найти ток, потребляемый от источника, можно зная, что в резисторе R2 выделяется мощность 24 Вт.

Из формулы мощности P=U ² / R, зная величину мощности P₂ и сопротивления R_2,  находим напряжение на резисторе R₂

Резисторы R2 и R3 соединены параллельно, поэтому напряжения на этих резисторах равны:  

U₂ =U₃

и можно найти токи в резисторах R2 и R3 по закону Ома:

I₂=U₂/R₂=12/6=2 А.

I₃ =U₃ / R₃ = 12 / 3 = 4A.

В резисторе R₁ протекает ток, равный сумме токов в резисторах R2 и R3

I₁ = I₂ +I₃ = 2+4 = 6А.

Ток в резисторе R₁ равен общему току, потребляемому от источника.

I₁=I_об=6А.

в) Отсюда напряжение на нагрузке источника (на резисторе Rоб)

U_об =I_об · R_об = 6·3,2 =19,2 В.

Полезная мощность, отдаваемая источником в нагрузку составляет:

Р_{полезн.}=I_об ²·R_об=6²·3,2=115,2 Вт.

г) Чтобы найти КПД источника необходимо знать величину ЭДС источника и полную мощность, отдаваемую источником.

Из закона Ома для полной цепи I = E/(R +r ₀) находим:

E=I(R_об+r₀)=6(3,2+1,2)=26,4 В.

Полная мощность

Р_полн=Е·I_об=26,4·6=158,4 Вт.

КПД источника

h=Р_полезн/Р_полн= 115,2/158,4=0,73 (73%).

д) Если резистор R₂ замкнуть накоротко, ток будет протекать мимо резисторов R₂ и R₃. общее сопротивление цепи уменьшится, а общий ток увеличится.

Новое значение КПД можно найти, используя уже рассмотренные приёмы.

Задача 8

    При правильной схеме подключения приборов (рис А) ток в цепи 12 А. Вольтметр показывает напряжение 120 В.

      Определить показания приборов, если вольтметр ошибочно включён в цепь последовательно с сопротивлением нагрузки, как показано на рисунке Б. Сопротивление вольтметра 1200 Ом. Сопротивление амперметра считать равным нулю, а напряжение на входе цепи неизменным.

Ответ: ток в цепи будет равен 0,01А и стрелка амперметра не отреагирует на столь малый ток; вольтметр покажет 119В.

Задача 9

В показанных ниже схемах а) и б) производится замыкание ключа S. Это вызывает включение третьей лампы, изменение токов в ветвях и, соответственно, изменение всех или некоторых яркости ламп.

Как изменятся яркости ламп HL₁ и HL₂ и ток I в цепях а)и б)?

Ответ обоснуйте формулами.

Ответы:

 в схеме а) яркость ламп не изменится;

 в схеме б) яркость лампы HL1 увеличится, яркость лампы HL2 уменьшится.

Задача 10*

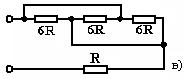
Определить эквивалентное (общее) сопротивление для каждой из цепей, показанных на рисунке.

В процессе решения задачи, при каждом упрощении схемы, перерисовывать схему заново. Записать процесс решения в виде формул.

Ответ: а) R_об = 2R; б) R_об = R; в) R_об = 3R; г). R_об = 4R; д) R_об = R.

 

                               

 

 

 

Задача 11*

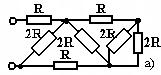
Какое соотношение несправедливо для цепи, изображённой на рисунке? Все резисторы одинаковы. Ответ обосновать формулами.

1. I₁ > I₂.

2. I₁ > I₃.

3. U₂ < U₁.

4. I₃ < I₂.

5. U₃ < U₂ < U.

 

Задача 12.

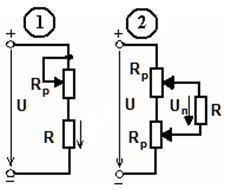
В какой из цепей с помощью перемещения движков реостатов можно регулировать напряжение потребителя U_п от нуля до полной величины U, действующего на входе цепи,  и изменять его полярность? Ответ обосновать формулами.

 

Задача   13*

Как изменятся показания приборов цепи при нагревании катушки, выполненной из медной проволоки, обладающей сопротивлением R_к?

Указать неправильный ответ. Ответ обосновать.

Ответ: 1. I₁ уменьшится.

2. I₂ не изменится.

3. I₃ уменьшится.

4. U₁ увеличится.

Задача 14

Ко входу цепи приложено постоянное напряжение 21 В.

 

Найти общее (эквивалент­ное) сопротивление цепи.Определить токв резисторе R₄ , если R₁= 5 Ом, R ₂= 2,5 Ом, R₃ = 8 Ом, R ₄= 3 om,  R ₅= 3 om.

 

Задача 15

В цепи известны сопротивления: R₁ = 10 Ом, R₂ = 15 Ом, R₃ = 25 Ом, R₄ = 50 Ом, R₅ = 5 Ом и ток I₁ == 2 А.

Определить токи  I₂, I₄, I₅   и напряжение на зажимах цепи.

 

Задача 16

В схеме делителя напряжения гасящее плечо составляет 200 Ом, а рабочее ­­­– 50 Ом.

Определить напряжение на выходе делителя, если входное напряжение в схеме 100 В, а нагрузка к делителю не подключена. Найдите мощность, выделяющуюся в каждом плече. Нарисовать схему делителя напряжения без нагрузки.

Повторите все вычисления для случая, когда к делителю подключена нагрузка величиной 150 Ом. Нарисовать схему делителя напряжения при подключении нагрузки.

 

   

 

 

 

Магнитная цепь

Задачи по магнитным цепям решаются с использованием закона Ома для магнитной цепи и закона полного тока. Кроме того, необходимо знать параметры магнитного поля и помнить формулы, связывающие эти параметры.

Пример 3.1 Расчёт магнитной цепи по закону полного тока.

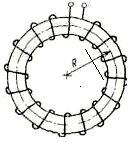Сердечник кольцевой катушки выполнен из ферромагнитного материала (электротехнической стали), имеет средний радиус R = 11 см и поперечное сечение S = 5 см². На сердечнике размещена обмотка, имеющая W = 690 витков. Определить ток в обмотке и магнитное сопротивление сердечника, если его магнитный поток Ф = 7*10 ^-4 Вб.

 

Решение.

Среднее значение магнитной индукции в сердечнике 

В = Ф / S = 7 · 10^-4 / (5 •10^-4) = 1,4 Тл.

Пользуясь кривой намагничивания электротехнической стали (график зависимости индукции В от напряжённости поля Н в сердечнике приведён в тексте решения примера 3.3.), определим значение напряженности соответствующее найденному значению индукции:

Н = 1000 А/м.

На основании закона полного тока I · W=H · L записываем:

                                 H · L= 1000 · 2p · 0,11 = 690 А 

(Здесь, в качестве длины контура L, в формулу подставлена длина средней силовой линии сердечника, определённая по формуле L=2p · R).

Из формулы закона полного тока находим ток в обмотке:

I = IW / W = 690 / 690 = 1A.

Абсолютная магнитная проницаемость

                m_a= В/Н = 1,4/1000 = 1,4 · 10 ^-3 Гн/м.

Магнитное сопротивление сердечника

 = 2p · 11 · 10^-2 / 1,4 · 10^-3 · 5 10^-4 = 9,9 · 10⁵ 1/Гн.

 

 

Пример 3.2 Расчёт индуктивности катушки.

Кольцевая катушка с неферромагнитным сердечником имеет следующие данные:

число витков W = 1000, средний радиус R = 10 см, поперечное сечение сердечника S = 20 см².     

Определить индуктивность катушки и ЭДС самоиндукции, если ток в катушке уменьшается со скоростью di/dt = 500 А/с, т.е. скорость изменения тока составляет 500А за секунду.

Решение.

Индуктивность катушки

                   .

 

ЭДС самоиндукции, индуктируемая в катушке,

e_L = -L · di/dt = 4 · 10 ^-3 · 500 = 2 В.

 

Пример 3.3. Расчёт магнитной цепи по закону полного тока.

При прохождении тока по обмотке, размещенной на кольцевом сердечнике из электротехнической стали, в сердечнике создается магнитное поле, индукция которого B= 1,4 Тл.

Размеры сердечника: диаметр поперечного сечения d=4 см, средний диаметр кольца d_ср=40 см.

Определить напряженность магнитного поля H, количество витков обмотки W, если по ней проходит ток I=5 А; магнитный поток Ф в сердечнике, индуктивность катушки L, относительную магнитную проницаемость сердечника μ.

 

Решение

Для решения задачи следует использовать кривую начального намагничивания электротехнической стали (см. рис.).

 

Зная величину индукции в сердечнике – 1,4 Тл., по кривой начального намагничивания для электротехнической стали, находим величину напряженности магнитного поля в сердечнике – 1000А/м.

По закону полного тока IW=HL находим число витков катушки

W=HL / I=1000·2p·0,2 / 5=251виток,

где L = 2p·R – длина средней силовой линии в магнитного поля в сердечнике (на рисунке соответствует пунктирной линии).

 

Магнитный поток в сердечнике

Ф = B·S = 1,4·0,000314 = 0,00044 Вб,

где S = pD² / 4 – площадь поперечного сечения сердечника.

 

Относительную магнитную проницаемость сердечника найдём из формулы

B = mm₀H,

откуда m = B / m₀H = 1,4 / 4p·10^-7·1000 = 1115.

 

Индуктивность катушки

L = mm₀W²S / L = 1115· 4p·10^-7·251² /2p·0,2 = 70 Гн.

Задача   17

От каких перечисленных ниже параметров, величин или свойств не зависит индуктивное сопротивление катушки?

1. Конфигурации катушки (длины и сечения катушки).

2. Числа витков катушки.

3. Относительной магнитной проницаемости сердечника катушки.

4. Частоты переменного тока, протекающего в катушке.

 

 

Задача 18

Сердечник кольцевой (в форме тора) катушки выполнен из ферромагнитного материала (электротехнической стали), имеет средний радиус R = 11 см и поперечное сечение S = 5 см². На сердечнике размещена обмотка, имеющая W = 690 витков. Напряжённость магнитного поля в сердечнике 2000А/м. Найти ток в катушке, магнитную индукцию, магнитную проницаемость сердечника и магнитный поток в сердечнике.

 

Задача 19

Кольцевая катушка с неферромагнитным сердечником имеет следующие данные: число витков W = 1000, средний радиус R = 20 см, поперечное сечение сердечника S = 10 см².     

Определить индуктивность катушки и ЭДС самоиндукции, если ток в катушке уменьшается со скоростью di/dt = 500 А/с, т.е. скорость изменения тока составляет 500А за секунду.

 

4. Однофазный переменный ток.

Задачи по теме однофазный ток требуют для решения понимания свойств основных параметров синусоидального тока, свойств элементов, входящих в цепь, возможных режимов работы цепи. Нужно уметь строить векторные диаграммы, знать способы сложения векторов.