, пусть элементы матрицы удовлетворяют следующим условиям:
1) В любой строке приращение между элементами матрицы
2) Строки расположены так, что
В этом случае оптимальное решение имеет следующий вид:
Пример
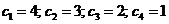
. Совершенно ясно, что 
.
Точные методы решения задач выбора
I. Метод линейного программирования
II. Вычислительная процедура динамического программирования
III. Венгерский метод
IV. Метод кратчайшего увеличивающегося пути (КУП)
V. Задача выбора с матрицей особого вида\
VI. Метод Мака
Метод линейного программирования
Предварительно проводится переиндексация переменных и коэффициентов матрицы:
Ограничения по строкам и столбцам:
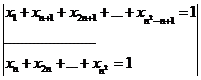
dim A =100, 
.
Вычислительная процедура динамического программирования
Введем функцию Беллмана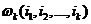 
- функция оптимального распределения К –работ между К -исполнителями, когда они имеют номера 
.
Функциональное уравнение Беллмана имеет вид:
Метод кратчайшего увеличивающегося пути (КУП)
Предположим, что существует оптимальное решение для матрицы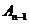 
, и его можно расположить по главной диагонали.
Перейдем к 
. Нужно добавить элемент для того, чтобы получить оптимальное решение.
Проанализируем пары: 
и 
.
Рассмотрим разность: - 
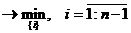- условие включения элемента в решение.
Если min соответствует 
, следовательно, в решение включаем элементы 
и 
.
Если min обеспечивается для 
, следовательно, в решение добавляем элемент 
.
Если решение для матрицы 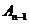будет оптимальным, то полученное решение будет оптимальным для матрицы .
В методе КУП последовательно наращивается порядок матрицы от 2 до n, в решение вводятся элементы по приведенным выше правилам.
Пример задачи выбора.
Пусть 
дает решение 
.
Дополним до матрицы .
i =1 (25+1)-(5+5)=16
i =2 (20+2)-(8+5)=9
i =3 (15+3)-(9+5)=4
i =4 (10+4)-(8+5)=4
i =5 5-5=0
min=0 
в решение попадает 
Порядок: от 2 до n.
.
Приближенные методы решения задач выбора
1) Метод поэтапного выбора
2) Метод Фогеля
3) Метод КУП
4) Задача выбора и «жадный» алгоритм
5) Метод приращений
6) Метод min (max) элемента при минимизации (максимизации) (частный случай «жадного» алгоритма)
и т.д.
Метод поэтапного выбора
Подсчитывается сумма элементов в каждой строке, строки расположены в порядке убывания этих сумм.
К -тый шаг: в К-той строке отыскивается минимальный элемент и вносится в решение. Соответствующий этому элементу столбец исключаем из матрицы, 
.
Пример
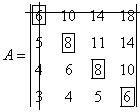
Эта матрица особого вида, следовательно, уже знаем решение.
- существует сигнал.
Метод Фогеля
1-ая итерация
1-ый шаг: в каждой строке определяется минимальный элемент и ближайший к нему элемент и составляются n -разностей.
2-ой шаг: в каждом столбце определяется минимальный и ближайший к нему элемент и составляются n -разностей.
3-ий шаг: Из 2 n элементов 
и 
выбирается максимальный. Пусть соответствующий элемент (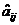
или 
) есть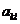 
.
2-ая итерация
Элемент 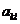вносится в искомое решение.
3-я итерация
Строка k и столбец l удаляются из матрицы.
К -ая итерация
Аналогично, но матрица имеет порядок n - k.
Замечания:
1. Если среди элементов и одинаковые максимумы, то анализируются соответствующие им минимальные элементы строки (столбца), из них выбирается минимум.
2. Если и они одинаковые ( и 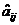), то выбирается 1-ый элемент в порядке просмотра.
Пример (рассматривается специальная матрица, имеющая точное решение)
1-ая итерация:
два одинаковых максимальных элемента и одинаковые соответствующие им минимальные элементы (6). Поэтому выбирается 1-ый элемент в порядке просмотра 
- в решение (
).
2-ая итерация:
- вносим в решение (
)
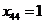3-я итерация:
- в решение (
)
4-ая итерация:
