Задачи, методы и алгоритмы IV-го иерархического уровня
Основные функции управляющего органа:
1) выбор состояния, в которое надо перевести систему;
2) выбор режима, в котором должна функционировать система;
3) принятие решений о выполнении нестандартной задачи;
4) формирование алгоритма принятия решений в плохо структурированных условиях:
a) когда формальных моделей нет;
b) когда векторов показателей, обладающих полнотой отражения вербальной цели, нет;
c) когда множество альтернатив точно не задано (альтернатива – множество, на котором мы принимаем решения);
5) принятие решений во внештатных ситуациях
средство реализации – элемент 
:
a) либо в виде автомата,
b) либо в виде ЛПР, обеспеченного системами подготовки решений или группами поддержки
Среди типовых задач, решаемых на уровне , выделяются задачи управления ресурсами, например:
1) распределение ресурсов
2) целераспределение
Основные ограничения при принятии решений:
1) 
,
2) 
Классическая задача принятия решений
Заключается в выборе допустимого или оптимального решения на декартовом множестве альтернатив (Y,H,U,P(X),G,D)
Y – множество входных неконтролируемых воздействий.
– множество допустимых управлений в ЗОУ, ЗИСО, ПР.
H – множество неопределенностей.
X – множество выходов или множество моделей P
Множество моделей: 
– множество выходов (состояний)
G – множество оценочных функций, где
(или Е) – множество оценок
D – множество допустимости (толерантности),
где 
, 
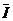– допустимые значения оценок (или других ограничений).
Формулировка задачи принятия допустимых решений
При заданном 
существует допустимое решение, если можно найти 
такие, что 
.
«
» – если вектор 
в функции G – потери;
«
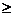» – если вектор имеет смысл эффективности.
Задача принятия оптимального решения
При заданном существуют оптимальные решения, если можно найти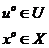 
такие, что 
(или 
, если – показатель эффективности)
Пример задачи принятия решений. (Задача выбора оптимального маршрута на основе нелинейного программирования)
Введем функцию, подобную функции Беллмана 
, определяющую оптимальное значение критерия для маршрута из 0 в К.
,
где р – множество вершин; 
- вес дуги из любой вершины Р в вершину К. Р<К – номера всех вершин, инцидентных вершине К, { K =0..N}.
Учитывая срецифику этого конкретного графа:
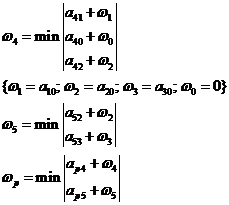
и т.д. (Идем по функциям, выбираем не единственный оптимальный маршрут.)
Методы решения задачи выбора (задачи назначения)
В общем случае задача принятия решения – неформализованная задача, для ее решения необходимо применить такой метод, как экспертные подходы.
В данном пункте мы будем рассматривать предварительно количественное обоснование решений на основе одного из видов задач распределения ресурсов:
· общая задача распределения ресурсов
· задача размещения
· задача назначения
Наиболее структуно простой является задача назначения:
существует n – исполнителей и n – работ
Матрица 
, где 
может иметь смысл времени, стоимости работ, дальности (расстояния) и т.д. или вероятности поражения (
- i -ое средство, т.е. снаряд, направляется на j -ую цель, где 
- эффективность поражения).
