Дано: F=30кН, q=40 кН/м, М=50кНм, а=2м, h=2м.
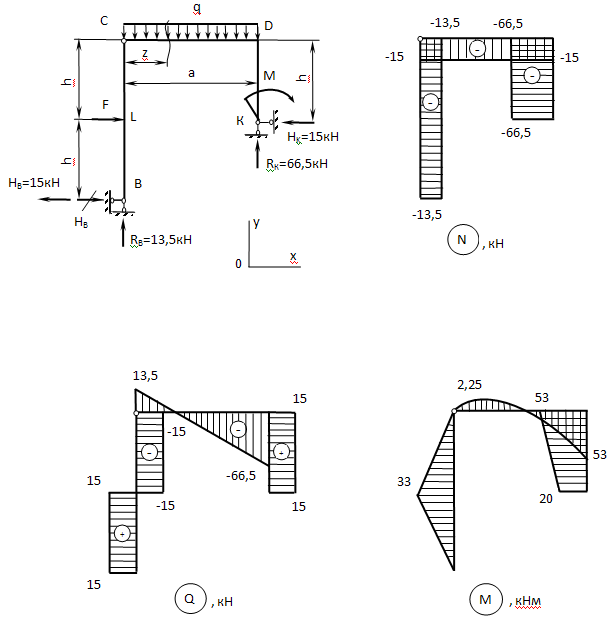
Решение. Определим опорные реакции. Следует отметить,что в обеих шарнирно-неподвижных опорах по две реакции. В связи с этим следует использовать свойство шарнира С — момент в нем как от левых,так и от правых сил равен нулю. Рассмотрим левую часть.
Уравнения равновесия для рассматриваемой рамы можно записать в виде:

Из решения данных уравнений следует:

На схеме рамы направление действия силы Н В изменяется на противоположное (Н B =15кН).
Определим усилия в характерных сечениях рамы.
Участок BZ: 
(сжаты левые волокна).
Участок ZC:

(сжаты левые волокна);
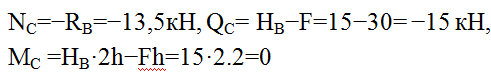
Участок КD: 
(сжаты левые волокна);
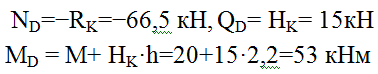
(сжаты левые волокна).
Участок DС:

(сжаты нижние волокна);

Определение экстремального значения изгибающего момента на участке CD:
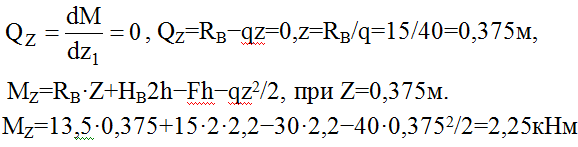
(сжаты верхние волокна).
Строим эпюры внутренних усилий. Проверяем равновесие узлов рамы. 
Узлы C и D находятся в равновесии.
Запись опубликована 16.10.2014 в рубрике Задачи на эпюры.
Задача 8
Построение эпюр М и Q в балке с жесткой заделкой с определенными опорными реакциями. Построение методом характерных точек.
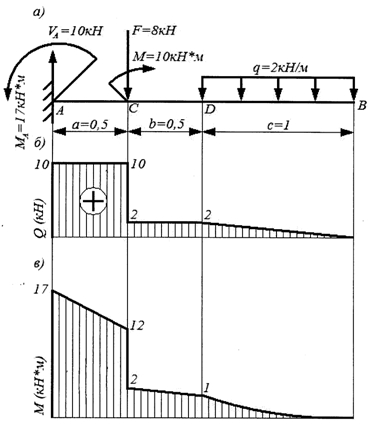
1. Построение эпюры поперечных сил. Для консольной балки (рис. а) характерные точки: А – точка приложения опорной реакции V A; С – точка приложения сосредоточенной силы; D, B – начало и конец распределенной нагрузки. Для консоли поперечная сила определяется аналогично двухопорной балке. Итак, при ходе слева:

Для проверки правильности определения поперечной силы в сечениях пройдите балку аналогичным образом, но с правого конца. Тогда отсеченными будут правые части балки. Помните, что правило знаков при этом изменятся. Результат должен получиться тот же. Строим эпюру поперечной силы (рис, б).
Построение эпюры моментов
Для консольной балки эпюра изгибающих моментов строится аналогично предыдущему построению.Характерные точки для этой балки (см. рис. а) следующие: А – опора; С — точка приложения сосредоточенного момента и силы F; D и В — начало и конец действия равномерно распределенной нагрузки. Поскольку эпюра Q x на участке действия распределенной нагрузки нулевую линию не пересекает, для построения эпюры моментов на данном участке (параболическая кривая) следует выбрать произвольно дополнительную точку для построения кривой, к примеру в середине участка.
Ход слева:
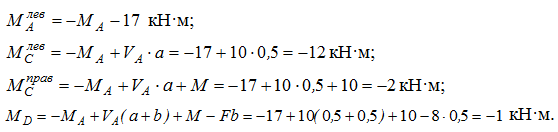
Ходом справа находим M B = 0.
По найденным значениям строим эпюру изгибающих моментов (см. рис. в).
Запись опубликована 14.09.2014 в рубрике Задачи, Задачи на изгиб, Задачи на эпюры.
Задача 7
Построение эпюр М и Q в балке на двух опорах с определенными опорными реакциями. Построение методом характерных точек.
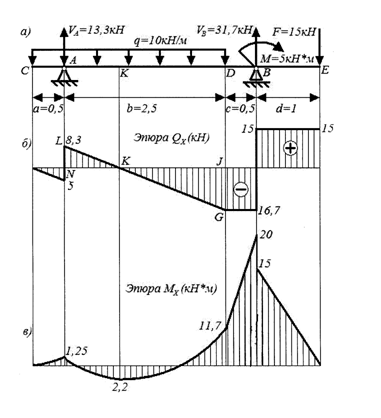
1. Построение эпюры Q у. Из теоретического курса известно, что на участке балки с равномерно распределенной нагрузкой эпюра Q у ограничивается наклонной прямой, а на участке, на котором нет распределенной нагрузки, — прямой, параллельной оси, поэтому для построения эпюры поперечных сил достаточно определить значения Q у в начале и конце каждого участка. В сечении, соответствующем точке приложения сосредоточенной силы, поперечная сила должна быть вычислена чуть левее этой точки (на бесконечно близком расстоянии от нее) и чуть правее ее; поперечные силы в таких местах обозначаются соответственно  .
.
Строим эпюру Q у методом характерных точек, ходом слева. Для большей наглядности отбрасываемую часть балки на первых порах рекомендуется закрывать листом бумаги. Характерными точками для двухопорной балки (рис. а) будут точки C и D – начало и конец распределенной нагрузки, а также A и B – точки приложения опорных реакций, E – точка приложения сосредоточенной силы. Проведем мысленно ось y перпендикулярно оси балки через точку С и не будем менять ее положение, пока не пройдем всю балку от C до E. Рассматривая левые отсеченные по характерным точкам части балки, проецируем на ось y действующие на данном участке силы с соответствующими знаками. В результате получаем: 
Для проверки правильности определения поперечной силы в сечениях можно пройти балку аналогичным образом, но с правого конца. Тогда отсеченными будут правые части балки. Результат должен получиться тот же. Совпадение результатов может служить контролем построения эпюры Q у. Проводим нулевую линию под изображением балки и от нее в принятом масштабе откладываем найденные значения поперечных сил с учетом знаков в соответствующих точках. Получим эпюру Q у (рис. б).
Построив эпюру, обратите внимание на следующее: эпюра под распределенной нагрузкой изображается наклонной прямой, под ненагруженными участками — отрезками, параллельными нулевой линии, под сосредоточенной силой на эпюре образуется скачок, равный значению силы. Если наклонная линия под распределенной нагрузкой пересекает нулевую линию, отметьте эту точку, то это точка экстремума, и она является теперь для нас характерной, согласно дифференциальной зависимости между Q у и М x, в этой точке момент имеет экстремум и его нужно будет определить при построении эпюры изгибающих моментов. В нашей задаче это точка К. Сосредоточенный момент на эпюре Q у себя никак не проявляет, так как сумма проекций сил, образующих пару, равна нулю.
2. Построение эпюры моментов. Строим эпюру изгибающих моментов, как и поперечных сил, методом характерных точек, ходом слева. Известно, что на участке балки с равномерно распределенной нагрузкой эпюра изгибающих моментов очерчивается кривой линией (квадратичной параболой), для построения которой надо иметь не менее трех точек и, следовательно, должны быть вычислены значения изгибающих моментов в начале участка, конце его и в одном промежуточном сечении. Такой промежуточной точкой лучше всего взять сечение, в котором эпюра Q у пересекает нулевую линию, т.е. где Q у = 0. На эпюре М в этом сечении должна находиться вершина параболы. Если же эпюра Q у не пересекает нулевую линию, то для построения эпюры М следует наданном участке взять дополнительную точку, к примеру, в середине участка (начала и конца действия распределенной нагрузки), помня, что выпуклостью парабола всегда обращена вниз, если нагрузка действует сверху вниз (для строительных специальностей). Существует правило «дождя», которое очень помогает при построении параболической части эпюры М. Для строителей это правило выглядит следующим образом: представьте, что распределенная нагрузка — это дождь, подставьте под него зонт в перевернутом виде, так чтобы дождь не стекал, а собирался в нем. Тогда выпуклость зонта будет обращена вниз. Точно так и будет выглядеть очертание эпюры моментов под распределенной нагрузкой. Для механиков существует так называемое правило «зонта». Распределенная нагрузка представляется дождем, а очертание эпюры должно напоминать очертания зонтика. В данном примере эпюра построена для строителей.
Если требуется более точное построение эпюры, то должны быть вычислены значения изгибающих моментов в нескольких промежуточных сечениях. Условимся для каждого такого участка изгибающий момент сначала определить в произвольном сечении, выражая его через расстояние х от какой-либо точки. Затем, давая расстоянию х ряд значений, получим значения изгибающих моментов в соответствующих сечениях участка. Для участков, на которых нет распределенной нагрузки, изгибающие моменты определяют в двух сечениях, соответствующих началу и концу участка, так как эпюра М на таких участках ограничивается прямой. Если к балке приложен внешний сосредоточенный момент, то обязательно надо вычислять изгибающий момент чуть левее места приложения сосредоточенного момента и чуть правее его.
Для двухопорной балки характерные точки следующие: C и D – начало и конец распределенной нагрузки; А – опора балки; В – вторая опора балки и точка приложения сосредоточенного момента; Е – правый конец балки; точка К, соответствующая сечению балки, в котором Q у = 0.
Ход слева. Правую часть до рассматриваемого сечения мысленно отбрасываем (возьмите лист бумаги и прикройте им отбрасываемую часть балки). Находим сумму моментов всех сил, действующих слева от сечения относительно рассматриваемой точки. Итак,

Прежде чем определить момент в сечении К, необходимо найти расстояние х=АК. Составим выражение для поперечной силы в данном сечении и приравняем его к нулю (ход слева):

Это расстояние можно найти также из подобия треугольников KLN и KIG на эпюре Q у (рис. б ).
Определяем момент в точке К:

Пройдем оставшуюся часть балки ходом справа.

Как видим, момент в точке D при ходе слева и справа получился одинаковый – эпюра замкнулась. По найденным значениям строим эпюру. Положительные значения откладываем вниз от нулевой линии, а отрицательные – вверх (см. рис. в).
Запись опубликована 14.09.2014 в рубрике Задачи, Задачи на изгиб, Задачи на эпюры.
Задача 6
Построение эпюр М и Q в балке с неравномерно распределенной нагрузкой. Построение методом сечений.

Определяем реакции. Задаёмся направлениями вертикальных опорных реакций А и В и определяем их из уравнений статики типа суммы моментов:

I участок (оставляем левую часть балки, начало отсчета располагаем на левой опоре)
 Здесь помним, что нагрузка имеет форму прямоугольного треугольника, центр тяжести которого приложен на расстоянии одной трети от прямого угла.
Здесь помним, что нагрузка имеет форму прямоугольного треугольника, центр тяжести которого приложен на расстоянии одной трети от прямого угла.

Найдем аналитический максимум функции изгибающего момента в пределах первого участка из условия:

II участок
 откуда
откуда  — это уравнение прямой.
— это уравнение прямой.
При z 2=0: M =0,
z 2=2м: M =-60кНм.
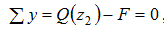
тогда Q (z 2)=F=30 кН – постоянная функция.
Заметим, что величина скачка в эпюре Q на правой опоре в точности соответствует самой правой опорной реакции.






