Подобрать стальную балку двутаврового поперечного сечения при R =160 МПа:
С эпюры берем максимальный момент:
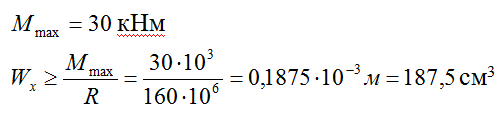
По сортаменту подбираем двутавр № 20 с 
Двутавр можно взять чуть меньше, при условии, что перенапряжение составляет меньше 5%:
Запись опубликована 20.12.2014 в рубрике Задачи на эпюры, Расчет на прочность.
Построение эпюр Q и М, проектировочный расчет (подбор сечения)
Для заданной балки требуется построить эпюры Q и M, найти M max и сделать проектировочный расчет — подобрать деревянную балку круглого поперечного сечения. Расчетное сопротивление материала R u =10 МПа.
1.Определение реакций:
Сумма проекций всех сил на ось z: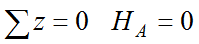 
Сумма проекций всех сил на ось y: 
Сумма моментов относительно точки А: 
После нахождения опорных реакций следует выполнить проверку, использовав уравнение равновесия (сумма моментов относительно любой выбранной точки должна быть равна нулю).
2. Записываем уравнения Q и M для каждого из участков в общем виде, при этом учитываем знаки.
Q — поперечная сила, считается положительной, если стремится повернуть рассматриваемую часть балки по часовой стрелке.
M — изгибающий момент, считается положительным, если растягивает нижние волокна.
1)Первый участок:
2) Второй участок:
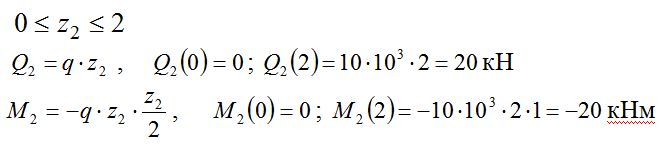
3) Третий участок:
Следует отметить,что на втором и третьем участке для построения плавной кривой потребуются дополнительные точки, в которых следует посчитать значение изгибающего момента.
Проектировочный расчет, то есть подбор размеров поперечного сечения.
Подберем деревянную балку круглого поперечного сечения при R u =10 МПа
С эпюры берем максимальный момент и рассчитываем требуемый осевой момент сопротивления, после чего вычисляем необходимый диаметр балки. 
Запись опубликована 20.12.2014 в рубрике Задачи на эпюры, Расчет на прочность.
Построение эпюр в балке с шарниром
Задача 1. Построить эпюры Q и M в балке с шарниром.
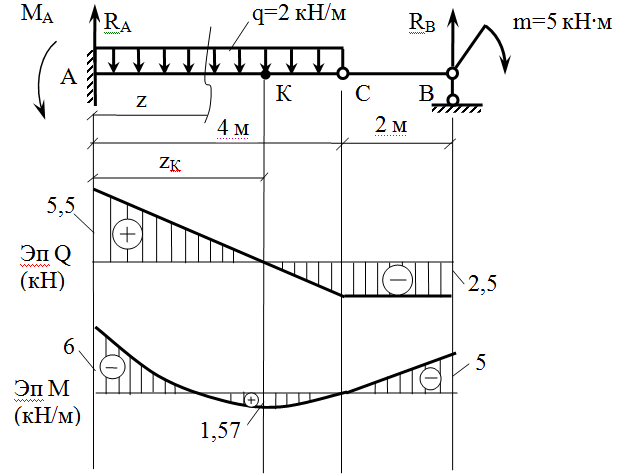
1. Определим опорные реакции. Для определения опорных реакций используем свойство шарнира – момент в нем как от левых, так и от правых сил равен 0.
Если рассмотреть левую часть, то в уравнении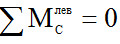 
будут присутствовать две неизвестные R А и М А. Значит, следует рассмотреть правую часть (из него найдем R В).
Теперь 
из него найдем М А
Следующее уравнение 
из него найдем R А
Строим эпюру Q.
Участок первый — АС, смотрим левую часть
Участок второй — СВ, смотрим правую часть
Строим эпюру М
Определим момент в точке, где Q=0 (момент имеет экстремум), это момент в точке К, т.е. М К , для этого определим положение точки К.
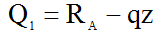Это уравнение первого участка, на котором находится точка К
в точке К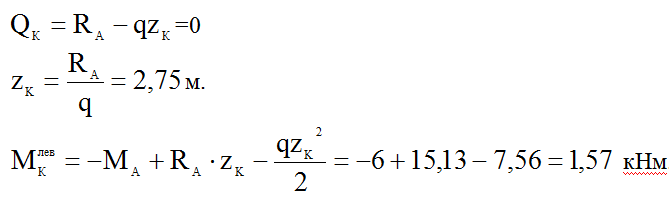 
Строим эпюры. Задача решена.
