Стандартное отклонение (sх) соответствует квадратному корню из дисперсии. Наряду с дисперсией является одной из наиболее часто используемых мер вариабельности признака.
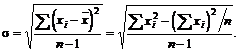(5.9)
Коэффициент вариации
Коэффициент вариации (V) есть отношение стандартного отклонения к среднему арифметическому значению, выраженное в процентах:
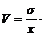100 % (5.10)
Задачи по теме
Задача 5. 1
В психофизиологическом эксперименте регистрировалось время простой сенсомоторной реакции у 50 испытуемых в ответ на звуковой стимул средней интенсивности. Получены следующие значения времени реакции (ВР) в миллисекундах:
| № | Т, мс | № | Т, мс | № | Т, мс | № | Т, мс | № | Т, мс |
| 1 2 3 4 5 6 7 8 9 10 | 138 180 160 144 169 140 178 134 141 174 | 11 12 13 14 15 16 17 18 19 20 | 137 172 143 126 139 130 127 144 125 132 | 21 22 23 24 25 26 27 28 29 30 | 136 132 135 142 129 139 156 130 141 175 | 31 32 33 34 35 36 37 38 39 40 | 142 164 147 144 131 150 128 143 133 151 | 41 42 43 44 45 46 47 48 49 50 | 149 158 145 155 161 148 166 146 128 153 |
Задание
1. Определить размах вариаций, междуквартильный и полумеждуквартильный размах, среднее отклонение, дисперсию, стандартное отклонение и коэффициент вариации.
2. Построить обычную и кумулятивную кривые распределения ВР. Определить процентное соотношение частот при нормировании распределения по стандартному отклонению от – 4 до + 4s с шагом в 1s.
3. Определить размах распределения признака в единицах стандартного отклонения.
Задача 5.2
Условие задачи
Проведено тестирование двух групп испытуемых (по 10 человек в каждой) на уровень личностной тревожности (УЛТ) по Спилбергеру. Получены следующие результаты:
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| УЛТ1 | 24 | 42 | 29 | 39 | 26 | 37 | 40 | 33 | 44 | 38 |
| УЛТ2 | 34 | 40 | 26 | 47 | 29 | 31 | 38 | 43 | 45 | 42 |
Задание
Определить средние значения УЛТ, стандартные отклонения и коэффициенты вариаций для каждой группы испытуемых, сравнить их между собой, сделать выводы.
РАЗДЕЛ 6.
РАСПРЕДЕЛЕНИЯ ПЕРЕМЕННЫХ ВЕЛИЧИН
В разделах 3 и 4 были даны основные представления о распределениях переменных величин (моно-, би-, полимодальные и др.). В этих случаях речь шла о характере эмпирических (экспериментальных) распределениях, которые могут иметь весьма разнообразный (зачастую непредсказуемый) характер. Подойдем к данному вопросу с несколько иной стороны. Кроме эмпирических (построенных на основе данных экспериментального исследования) существуют и теоретические распределения. Любое теоретическое распределение представляет собой определенную математическую модель, которой (с определенной долей вероятности) могут соответствовать (или не соответствовать) экспериментальные распределения. Перед психологом достаточно часто возникает проблема сопоставления экспериментального распределения с теоретическим – в плане выбора наиболее адекватного метода математической обработки результатов (см. раздел 7), для прогнозирования вероятности тех или иных событий и т. д. В данной главе будут рассмотрены лишь те виды распределений, с которыми психологам приходится встречаться особенно часто. Особое внимание будет уделено нормальному распределению. Кроме него, будут рассмотрены равномерное, биномиальное распределение и распределение Пуассона.
Нормальное распределение
6. 1. 1. Основные понятия
Нормальное распределение (распределение Гаусса, распределение Муавра – Лапласа) – это распределениезначенийпеременной величины в тех случаях, когда она варьирует случайным образом и не подвержена влиянию какого-либо систематического фактора.
Формула нормального распределения:
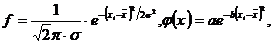(6.1 а, б)
где: f – теоретическая частота встречаемости значения xi; s – стандартное отклонение; a, b – константы; p» 3,142 (отношение длины окружности к диаметру); e» 2,718 (основание натурального логарифма).
Теоретическое нормальное распределение имеет вид симметричной колоколообразной кривой, которая подчиняется следующим закономерностям:
1. Правая и левая ветви теоретического нормального распределения абсолютно симметричны и как бы зеркально отражают друг друга.
2. В нормальном распределении основные показатели центральной тенденции (мода, медиана и среднее арифметическое значение) совпадают и соответствуют самой высокой точке (вершине) распределения.
3. Правая и левая ветви распределения уходят в бесконечность, никогда не соприкасаясь с осью абсцисс. Другими словами, частота (вероятность) встречаемости того или иного значения признака может быть сколь угодно мала, но никогда не равна нулю. В практическом отношении это свойство нормального распределения весьма неудобно, так как погоня за бесконечностью – занятие весьма неблагодарное. Поэтому принято анализировать полученные данные в диапазоне от –4 до +4 стандартных отклонений (теоретически в этот диапазон должно попадать ~ 99,98% экспериментальной выборки). В то же время сужение диапазона до ±3 σ несколько рискованно, так как значения, даваемые «крайними» испытуемыми, могут выпасть из рассмотрения.
При переводе экспериментальных значений в единицы стандартного отклонения может быть использована мера Пирсона z = (x i -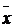 
)/sх. На рис. 6.1 показаны теоретические частоты встречаемости значений признака (в процентном соотношении) при разбиении диапазона от –4 до +4 s на восемь равных классов (ширина каждого класса соответствует одному стандартному отклонению), а также соответствующие 8-классовому распределению кумулятивные (накопленные) частоты (рис. 6.2). Эти численные значения могут понадобиться для сравнения экспериментально полученного распределения с теоретическим.
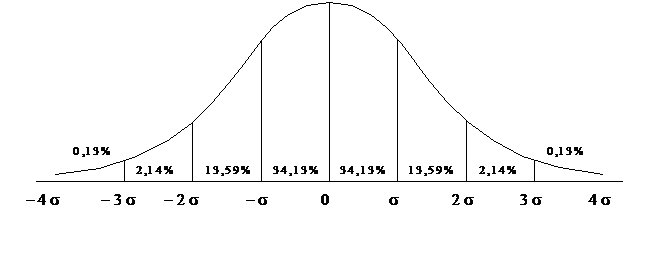Рис. 6.1. Кривая нормального распределения
»0,1%»2,3%»15,9%»50%»84,1%»97,7%»99,9%»100%
Рис. 6.2. Кумулятивная кривая нормального распределения
Кроме 8-классового, иногда используют 16-классовое распределение – в этом случае диапазон от –4 до +4 s разбивают на 16 равных классов с шагом 0,5 стандартных отклонения.
Зная распределение частот в нормальном распределении, можно решить обратную задачу – определить размах (в единицах стандартного отклонения), в который укладывается определенное количество (процент) значений выборочной совокупности. Так, 90% выборки укладываются в пределах ±1,645s; 95% соответствуют ±1,96s; 99% соответствуют ±2,58s;99,9% укладываются в ±3,29s. Как будет показано далее, эти соотношения имеют большое значение для определения достоверности некоторых статистических выводов при разных уровнях значимости.
Двумерное нормальное распределение можно получить, измеряя две относительно независимые друг от друга переменные. Оно строится в трехмерном пространстве, в координатах f (x, y) и имеет колоколообразный вид.
Как отмечалось ранее, распределения переменных величин, получаемые в эксперименте, имеют определенную степень приближения к теоретическому (нормальному) распределению. В данном случае степень соответствия эмпирического распределения нормальному позволяет определить, насколько случайно или закономерно варьирует тот или иной показатель, подвержен ли он влиянию каких-либо систематических факторов и т. д.
Существует ряд статистических критериев, позволяющих сравнить экспериментально полученное распределение с теоретическим (нормальным). Основными из них являются коэффициент асимметрии, показатель эксцесса, критерий хи-квадрат Пирсона (c 2) и критерий lКолмогорова - Смирнова.
6. 1. 2. Коэффициент асимметрии
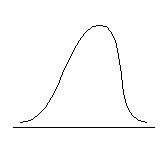
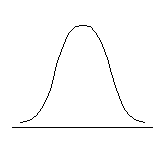
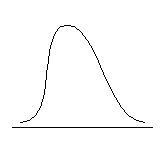
Распределение может быть приблизительно симметричным относительно моды либо обладать отрицательной или положительной асимметрией. Положительно асимметричным считается распределение с более крутым левым и более пологим правым крылом, распределение с отрицательной асимметрией, напротив, имеет более пологий левый фронт нарастания и более крутой правый (см. рис. 6.3.).
| 
| 
|
| Отрицательная асимметрия, As < 0 | Симметричное распределение, As = 0 | Положительная асимметрия, As > 0 |
Рис. 6.3. Типы асимметрии
Рассчитываемый по соответствующим формулам коэффициент асимметрии (As) может быть использован в качестве одного из критериев соответствия экспериментального распределения теоретическому.
Вычисление коэффициента асимметрии:
Коэффициент асимметрии вычисляется по следующей формуле:
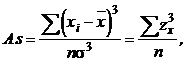(6.2)
где z x – мера Пирсона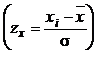 
.
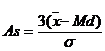При больших выборках (n > 50) можно использовать упрощенную формулу:
(6.3)
Соответствие эмпирического распределения нормальному находится по соответствующим таблицам (в нашем приложении – табл. I). При этом эмпирическое распределение считается соответствующим теоретическому (нормальному), если асимметрия при данной выборке не превышает граничного значения.
Пример
Распределение значений исследуемого признака для выборки в 100 человек обнаружило коэффициент асимметрии As = 0,55.
Вопрос: соответствует ли данное распределение нормальному?
Решение: в табл. I находим, что для n = 100 As кр. = 0,39 (для b1 = 0,95) и As кр. = 0,57 (для b1 = 0,95).
Ответ: распределение статистически достоверно отличается от нормального с вероятностью 0,95, поскольку As эксп.> As кр. С вероятностью же 0,99 аналогичного вывода мы сделать не можем(As эксп. < As кр.).
Причины асимметрии могут быть различными. Во-первых, это возможное действие побочных однонаправленных факторов. Так, например, в тестах на измерение интеллекта могут преобладать сложные задания, с которыми большинство испытуемых не справляется. Это может явиться причиной положительной асимметрии (центральная тенденция лежит слева от среднего значения). Во-вторых, это ограничение (сверху или снизу) размаха вариаций. Например, при измерении времени сенсомоторной реакции нижний предел реагирования лимитирован физиологическими возможностями субъекта, в то время как верхний жестко не ограничен. Наконец, третьей причиной асимметрии может быть неоднородность выборки (например, если исследование проводится в смешанной группе разного возраста). При этом имеет место наложение друг на друга двух или нескольких разных по численности и сдвинутых относительно друг друга по моде распределений.
Коэффициент эксцесса
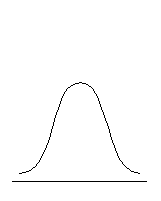
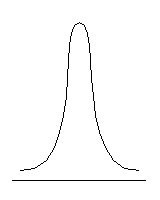
В отличие от коэффициента асимметрии, коэффициент (показатель) эксцесса характеризует компактность или «размытость» распределения, его островершинность или плосковершинность, что связано с разным характером группирования значений переменной вокруг среднего (рис. 6.4).
| 
| 
|
| Плосковершинное распределение, Ex < 0 | Нормальное распределение, Ex = 0 | Островершинное распределение, Ex > 0 |
Рис. 6.4. Типы эксцесса
Причинами эксцесса могут быть большая или меньшая степень тяготения переменных к центральной тенденции, неоднородность выборки, наложение друг на друга нескольких распределений с одинаковой модой и разной дисперсией и т. д.
Вычисление показателя эксцесса
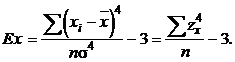(6.4)
Теоретически величина эксцесса может варьировать от – 3 до + ¥. Критерий согласия с нормальным распределением аналогично коэффициенту асимметрии определяется по таблицам граничных значений. Например, для n = 100 и b1 = 0,95 Ex кр = 0,83 (см. Приложение, табл. II).
Аналогично определению асимметрии распределение соответствует нормальному (согласуется с нормальным), если Ex < Ex кр. При обратном соотношении принято говорить, что по показателю эксцесса эмпирическое распределение статистически достоверно отличается от нормального.
При анализе эмпирического распределения может возникнуть такая ситуация, когда по одному из показателей (асимметрии или эксцессу) распределение соответствует нормальному, по другому же – отличается от него. В этом случае следует использовать следующее правило: если хотя бы по одному из вышеуказанных показателей распределение достоверно отличается от нормального, то следует делать вывод о том, что экспериментальное распределение отличается от теоретического (нормального).
Кроме коэффициента асимметрии и показателя эксцесса, для сравнения экспериментального распределения с теоретическим используют и другие критерии, в частности критерий хи-квадрат и критерий l Колмогорова - Смирнова.
6. 1. 4. Критерий хи-квадрат (c 2)
Критерий хи-квадрат основан на сравнении между собой эмпирических (экспериментальных) частот исследуемого признака и теоретических частот нормального распределения. Для сравнения частот можно пользоваться как 8-классовым, так и 16-классовым распределениями, теоретические частоты которых в интервале от – 4 до + 4 стандартных отклонений даны в приложении (табл. III и IV). В случае необходимости можно вычислять хи-квадрат и по большему числу классов – для этого используют специальные таблицы нормального распределения.
Критерий c2 рассчитывают по следующей формуле:
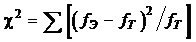, (6.5)
Где f э и f т – соответственно, экспериментальные и теоретические частоты в каждом отдельном классе разбиения. Полученное значение сравнивается со стандартным (табличным). Решение о соответствии экспериментального распределения теоретическому принимается, если c2 < χ2кр.при соответствующем числе степеней свободы и заданном уровне значимости. При этом необходимо иметь в виду, что в случае нормального распределения число степеней свободы (n) принимается равным N – 3, где N – число классов (групп разбиения).
Рассмотрим алгоритм вычислений критерия c2 на следующем примере.
Условие задачи
У 100 испытуемых определялся уровень нейротизма по тесту Айзенка. Получены следующие результаты (табл. 6.1):
Таблица 6.1
| Нейро-тизм | Число испытуе-мых | Нейро-тизм | Число испытуе-мых | Нейро-тизм | Число испытуе-мых | Нейро-тизм | Число испытуе-мых |
| xi | f э | xi | f э | xi | f э | xi | f э |
| 1 2 3 4 5 6 | 0 0 0 0 2 3 | 7 8 9 10 11 12 | 3 4 6 8 9 7 | 13 14 15 16 17 18 | 10 8 9 9 8 6 | 19 20 21 22 23 24 | 4 3 1 0 0 0 |
Задание
Определить соответствие экспериментального распределения теоретическому (нормальному) распределению с помощью критерия χ2 Пирсона.
Решение
Задача решается в три этапа:
1. Определяем среднее значение переменной и ее стандартное отклонение. Поскольку в данном случае мы имеем дело со сгруппированными частотами, то для вычисления среднего арифметического следует использовать следующую формулу (см. раздел 4):
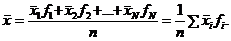
Подставляем в формулу значения нейротизма и соответствующие ему частоты из условия задачи:
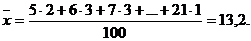
Стандартное отклонение следует определять по следующей формуле:
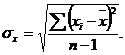(см. раздел 5)
В нашем случае:
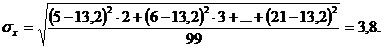
2. Нормируем полученные результаты в единицах стандартного отклонения с «шагом» в 1σ (8-классовое распределение). Для этого строим шкалу значений в единицах стандартного отклонения от –4 до + 4σ. Далее определяем границы каждого из 8 классов в абсолютных значениях исследуемого показателя (уровней нейротизма). Напомним, что точкой отсчета в данном случае является центральное значение (σх = 0), которому теоретически должны соответствовать основные меры центральной тенденции – мода, медиана и среднее арифметическое значение (см. подраздел 6.1.1). Обозначим среднюю точку значением 13,2 (среднее арифметическое). После этого определяем границы классов в абсолютных единицах (значениях нейротизма), последовательно вычитая из среднего (слева от нулевой точки) или добавляя к среднему (справа от нее) величину стандартного отклонения (σх = 3,8). Наконец, подсчитываем частоты (число испытуемых) в каждом из классов и разносим полученные значения по классам теоретического распределения. Для большей наглядности можно представить результаты в виде следующей схемы:
– 4 σ – 3 σ – 2 σ – σ 0 σ 2 σ 3 σ 4 σ
-2,0 1,8 5,6 9,4 13,2 17,0 20,8 24,6 28,4
3. Составляем таблицу для вычисления критерия χ2 Пирсона (см. табл. 6.2). В столбце 1 обозначаем классы распределения (в единицах стандартного отклонения, в столбце 2 – подсчитанные нами экспериментальные частоты в каждом классе, в столбце 3 – теоретические частоты в процентном соотношении (см. табл. III Приложения). Столбец 4 служит для попарного сопоставления экспериментальных и теоретических частот: для этого следует использовать формулу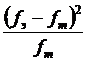 
Таблица 6.2
| Границы класса | Частоты |
| |
| f э | f т | ||
| 1 | 2 | 3 | 4 |
| – 4 σ ÷ – 3 σ – 3 σ ÷ – 2 σ – 2 ÷ – σ – σ ÷ 0 0 ÷ σ σ ÷ 2 σ 2 ÷ 3 σ 3 ÷ 4 σ | 0 2 16 34 30 17 1 0 | 0,13 2,15 13,59 34,13 34,13 13,59 2,15 0,13 | 0,13 0,01 0,43 0 0,50 0,86 0,62 0,13 |
Критерий χ2вычисляется как сумма значений в столбце 4 таблицы. Проводим соответствующие вычисления:
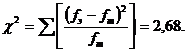
В табл. VI Приложения находим стандартные (критические) значения χ2. Напомним, что для 8-классового распределения (N = 8) число степеней свободы ν = N – 3 = 5. При этом стандартные значения χ2ст. для двух уровней значимости составляют, соответственно, 11,070 (β1 = 0,95) и 15,086 (β2 = 0,99).
Вывод
Для двух стандартных уровней значимости χ2 < χ2ст., следовательно, по критерию χ2 Пирсона экспериментальное распределение статистически не отличается от теоретического (нормального) распределения или, другими словами, соответствует последнему. Данный вывод можно считать справедливым для уровня значимости 0,99.
Примечания
1. Если по каким-либо причинам результаты анализа не удовлетворяют исследователя (например, χ2 ≈ χ2ст.), можно воспользоваться таблицей 16-классового распределения (см. Приложение, табл. IV). В данном случае диапазон вариаций также составляет –4 ÷ +4σ, но ширина каждого класса вдвое меньше (0,5 стандартного отклонения). Кроме того, следует учесть, что при сравнении экспериментального значения хи-квадрат с критическим число степеней свободы в данном случае составляет N – 3 = 13.
2. Необходимо помнить о том, что теоретические частоты в табл. III и IV Приложения рассчитаны в процентном соотношении. При решении задачи анализа распределения испытуемых по уровню нейротизма объем выборки составлял 100 человек, поэтому никаких дополнительных преобразований не требовалось. В том же случае, когда n ≠ 100, необходимо уравнять частоты. При этом необходимо соблюдать правило, согласно которому экспериментальные частоты должны быть приведены к теоретическим (но не наоборот). Например, если n = 200, то экспериментальную частоту в каждом классе следует разделить на 2, если n = 50, то умножить на 2, а если, предположим, n = 52, то необходимо каждую экспериментальную частоту умножить на пересчетный коэффициент (в данном случае k = 100:52 = 1,923).
6. 1. 5. Критерий Колмогорова – Смирнова (l)
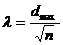Критерий Колмогорова – Смирнова основан на том же принципе, что и критерий χ2 Пирсона, но предполагает сопоставление накопленных частот экспериментального и теоретического распределений. Вычисляется как отношение максимальной разности (без учета знака) между теоретической и экспериментальной накопленной частотой к корню квадратному из численности выборки: (6.6)
Для вычисления l также можно воспользоваться таблицами теоретических частот 8- и 16-классового распределения. Рассмотрим алгоритм вычислений критерия Колмогорова на примере предыдущей задачи (табл. 6.3).
Таблица 6.3
| Границы класса | Экспериментальные частоты | Накопленные частоты | d | |
| F э | F т | |||
| 1 | 2 | 3 | 4 | 5 |
| – 4 σ ÷ – 3 σ – 3 σ ÷ – 2 σ – 2 ÷ – σ – σ ÷ 0 0 ÷ σ σ ÷ 2 σ 2 ÷ 3 σ 3 ÷ 4 σ | 0 2 16 34 30 17 1 0 | 0 2 18 52 82 99 100 100 | 0,13 2,28 15,87 50,00 84,13 97,72 99,87 100 | 0,13 0,28 2,13 2,00 2,13 1,28 0,13 0 |
Столбцы 1 и 2 аналогичны таковым в предыдущей таблице. Столбец 3 соответствует экспериментальным частотам, накопленным путем суммирования частот от 1-го до 8-го класса. Теоретические накопленные частоты взяты из табл. III Приложения. Максимальная разность между экспериментальной и теоретической накопленными частотами (столбец 5) соответствует 2,13. Проводим соответствующие вычисления:
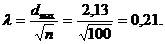
Для определения соответствия экспериментального распределения теоретическому по критерию Колмогорова можно воспользоваться следующим правилом. Если l < 0,52, делается вывод о соответствии распределений для уровня значимости 0,95. При l > 1,36 распределение достоверно отличается от нормального. При значениях же l от 0,52 до 1,36 (интервал неопределенности) можно определить вероятность соответствия экспериментального распределения теоретическому по табл. VII Приложения.
Вывод
Полученное нами значение λ = 0,21 < 0,52, следовательно, по критерию Колмогорова экспериментальное распределение соответствует нормальному с вероятностью 0,95.
Для определения соответствия эмпирического распределения теоретическому (нормальному) распределению можно воспользоваться и другим способом, который зачастую дает более точные результаты, поскольку не ограничен числом классов. Этот способ будет нами рассмотрен на примере той же задачи.
Порядок вычислений приводится в табл. 6.4.
1. В столбце 1 таблицы фиксируем значения xi (уровень нейротизма).
2. Переводим значения xi в меру z Пирсона по формуле: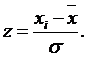 
3. Ориентируясь на условие задачи, вносим экспериментальные частоты в столбец 3.
4. По значениям столбца 3 вычисляем накопленные экспериментальные частоты и фиксируем их в столбце 4.
5. По значениям z Пирсона определяем теоретические накопленные частоты, для чего используем табл. V Приложений.
6. Вычисляем критерий d, сравнивая между собой экспериментальные (столбец 4) и теоретические частоты по формуле: d = │ F эксп. – F теор.│.
7. Вычисляем критерий λ Колмогорова по стандартной формуле.
Ответ
λ = 7,57:10 = 0,76 (столбец 6 таблицы), что соответствует интервалу неопределенности 0,52 ÷ 1,36.
С целью устранения случайных факторов используем процедуру интервальной нормализации 
(столбец 7) и повторно вычисляем критерий λ:
λ* = 4,64: 10 = 0,46 (столбец 8 таблицы).
Общий ответ
Эмпирическое распределение соответствует теоретическому (нормальному) распределению.
Таблица 6.4
| x i | Z | f э | F э | F т | d | F э * | d * |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | -3,2 -2,9 -2,7 -2,4 -2,2 -1,9 -1,6 -1,4 -1,1 -0,8 -0,6 -0,3 0 0,2 0,5 0,7 1,0 1,3 1,5 1,8 2,1 2,3 2,5 2,8 | 0 0 0 0 2 3 3 4 6 8 9 7 10 8 9 9 8 6 4 3 1 0 0 0 | 0 0 0 0 2 5 8 12 18 26 35 42 52 60 69 78 86 92 96 99 100 100 100 100 | 0,07 0,18 0,34 0,82 1,40 2,88 5,49 8,08 13,57 21,19 27,43 38,21 50,00 57,92 69,14 75,80 84,13 90,31 93,31 96,40 98,21 98,92 99,37 99,75 | 0,07 0,18 0,34 0,82 0,60 2,12 2,51 3,92 4,43 4,81 7,57 3,79 2,00 2,08 0,14 2,20 1,87 1,69 2,69 2,60 1,79 1,08 0,63 0,25 | 0 0 0 0 1 3,5 6,5 10 15 22 30,5 38,5 47 56 64,5 73,5 82 89 94 97,5 99,5 100 100 100 | 0,07 0,18 0,34 0,82 0,40 0,62 1,01 1,92 1,43 0,81 3,07 0,29 3,00 1,92 4,64 2,30 2,13 1,31 0,69 1,10 1,29 1,08 1,63 0,25 |
Равномерное распределение
В ряде случаев психологу приходится иметь дело с равномерным распределением, когда варьирующая величина (переменная) приблизительно с равной вероятностью принимает любое значение в определенном фиксированном диапазоне от x min до x max. Пример такого распределения приводится на рис. 6.5.
Рис. 6.5. Графическое выражение теоретического равномерного распределения (пояснения в тексте)
Примером равномерного распределения может служить распределение испытуемых по квантилям, поскольку в каждом интервале квантильной шкалы частоты встречаемости признака одинаковы.
Работа с равномерным распределением достаточно проста. Учитывая, что общая площадь распределения соответствует Р = 1, вероятность события в интересующем нас диапазоне x 1 ¸ x 2 равна отношению ширины этого диапазона (размаха вариаций) x 2- x 1 к общему (x max¸ x min). Для сравнения экспериментального распределения с теоретическим можно использовать критерий хи-квадрат, а при достаточном количестве эмпирических частот и критерий Колмогорова. Рассмотрим использование этих критериев на двух примерах.
Пример 1
Можно априорно предположить, что число людей, обладающих одним из четырех основных типов темперамента (холерики, сангвиники, флегматики и меланхолики) приблизительно одинаково. Для проверки этой гипотезы проведено тестирование по тесту-опроснику Айзенка 100 взрослых испытуемых. Тип темперамента определялся у них по соотношению показателей экстраверсии и нейротизма.
Было получено следующее распределение испытуемых по типам темперамента: холерики – 22 человека, сангвиники – 36, флегматики – 13 и меланхолики – 29 человек.
Задача состоит в том, чтобы либо принять, либо отвергнуть изначальную гипотезу (нуль-гипотезу) о равномерности распределения людей по типам темперамента.
Для решения задачи можно составить таблицу, аналогичную той, которая использовалась для оценки согласия эмпирического распределения с нормальным по критерию хи-квадрат (см. табл. 6.5).
Таблица 6.5
| Тип темперамента | Частота | (f эксп - f теор)2 f теор | |
| f эксп | f теор | ||
| Холерики (экстраверты с высоким уровнем нейротизма) Cангвиники (эмоционально стабильные экстраверты) Флегматики (эмоционально стабильные интроверты) Меланхолики (интроверты с высоким уровнем нейротизма) | 22 36 13 29 | 25 25 25 25 | 0,36 4,84 5,76 0,64 |
В данном случае следует пояснить, что теоретические частоты рассчитываются, исходя из гипотезы о том, что распределение по типам темперамента является идеально равномерным.
Вычисление показателя c2 (сумма значений в последнем столбце таблицы) дает величину 11,6. При сравнении полученного значения со стандартным (табл. VI Приложений) следует иметь в виду, что для равномерного распределения число степеней свободы вычисляется как число групп (классов) разбиения минус единица: в нашем случае n = N – 1 = 3.
Полученное нами значение (c2 = 11,6) больше стандартных (критических) значений как для 1-го (c2ст= 7,815), так и для 2-го уровня значимости (c2ст= 11,345). Отсюда следует, что принять гипотезу о равномерности распределения людей по типам темперамента мы не можем. Другими словами, распределение статистически достоверно отличается от равномерного.
Примечания
4. Критерий c2 дает надежные результаты на выборках более 30 человек. На малых выборках (n ≤ 30) критерий может «пробуксовывать» и данные могут быть подвергнуты сомнению.
2. Если число градаций признака равно двум, в формулу вычисления c2 необходимо вводить соответствующую поправку (так называемую поправку на непрерывность): (f эксп - f теор – 0,5)2
f теор
Пример 2
Условие задачи
В выборке здоровых лиц мужского пола, студентов технических вузов в возрасте от 19 до 22 лет проводился тест М. Люшера в 8-цветном варианте. Установлено, что желтый цвет предпочитается испытуемыми чаще, чем отвергается (см. табл. 6.6).
Таблица 6.6
| Разряды | Позиции желтого цвета | Сумма | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| Эмпирические частоты | 24 | 15 | 13 | 8 | 15 | 10 | 9 | 8 | 102 |
Вопрос
Можно ли утверждать, что распределение желтого цвета по восьми позициям у здоровых испытуемых отличается от равномерного распределения?
Решение
Для определения соответствия эмпирического распределения теоретическому (равномерному) можно использовать критерий Колмогорова. Для этого вносим экспериментальные данные в таблицу (табл. 6.7) и проводим стандартные вычисления.
Таблица 6.7
| Позиции желтого цвета | Частоты | Накопленные частоты |
d | ||
| f эксп | f теор | F эксп. | F теор. | ||
| 1 2 3 4 5 6 7 8 | 24 15 13 8 15 10 9 8 | 12,75 12,75 12,75 12,75 12,75 12,75 12,75 12,75 | 24 39 52 60 75 85 94 102 | 12,75 25,50 38,25 51,00 63,75 76,50 89,25 102 | 11,25 13,50 13,75 9,00 11,25 8,50 4,75 0 |
Отсюда: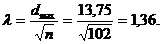 
Вывод
Экспериментальное распределение не соответствует теоретическому (равномерному) распределению.
