Условие максимума (2.10) позволяет найти управление u как функцию параметров 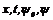 . Тогда мы получаем систему дифференциальных уравнений
. Тогда мы получаем систему дифференциальных уравнений
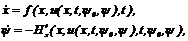 (2.12)
(2.12)
Объединяющую систему уравнений движения объекта и сопряженную систему.
Как известно, общее решение системы (2.12), состоящей из 2 n обыкновенных дифференциальных уравнений первого порядка, зависит от 2 n параметров. Кроме того, система необходимых условий оптимальности содержит m параметров 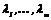 и параметр
и параметр 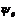 . Таким образом, общее число неизвестных равно 2 n + m +1.
. Таким образом, общее число неизвестных равно 2 n + m +1.
Для их определения мы имеем 2 n условий (2.11) и m условий (2.8). Еще одно условие определяется из следующих соображений. Легко понять, что в силу линейности функции H по переменным 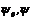 , теорема определяет вектор
, теорема определяет вектор 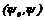 с точностью до положительного постоянного множителя. Поэтому если в конкретной задаче удается показать, что
с точностью до положительного постоянного множителя. Поэтому если в конкретной задаче удается показать, что 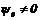 , то полагают обычно
, то полагают обычно 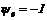 .
.
В противном случае накладывают какое-либо условие нормировки, например,  .
.
Таким образом, общее число условий равно 2 n + m +1 и совпадает с числом неизвестных параметров, что позволяет решить данную систему. Подобные рассуждения дают возможность в простейших случаях решить задачу оптимального управления в явном виде.
В результате применения изложенных теорем можно составить следующий алгоритм решения задачи оптимального управления на основе принципа максимума Понтрягина.
1) Составить гамильтониан (функцию Понтрягина)
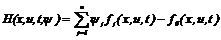 .
.
2) Найти структуру оптимального управления 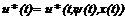 из условия максимума гамильтониана по управлению.
из условия максимума гамильтониана по управлению.
3) Составить систему канонических уравнений (2.12) с заданными в задаче условиями.
4) Из условий трансверсальности (2.11) получить недостающие краевые условия для уравнений составленной системы.
5) Решить двухточечную краевую задачу для системы канонических уравнений, полученную в п.3, с учетом пп. 2 и 4. В итоге определяется оптимальная траектория x *(t), оптимальное управление u *(t) (в зависимости от условия задачи и оптимальное время окончания процесса T).
Пример (простейшая задача оптимального быстродействия).
Пусть точка движется по прямой в соответствии с законом
 ,
,
где x – координата. Требуется найти управление u, переводящее точку из начального положения в начало координат за минимальное время T. При этом скорость точки в конце траектории должна быть нулевой, а управление – удовлетворять условию
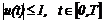 .
.
Применим к сформулированной задаче принцип максимума Понтрягина. Введем фазовые переменные 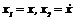 . Тогда движение управляемого объекта описывается системой двух дифференциальных уравнений первого порядка:
. Тогда движение управляемого объекта описывается системой двух дифференциальных уравнений первого порядка:
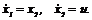 (2.13)
(2.13)
Начальное положение  при
при  и конечное положение (0,0) фиксированы, а конечный момент времени T не фиксирован, на управление наложено ограничение
и конечное положение (0,0) фиксированы, а конечный момент времени T не фиксирован, на управление наложено ограничение 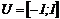 . Функционал качества управления имеет вид
. Функционал качества управления имеет вид
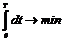 .
.
Сравнивая с постановкой задачи (2.7), получим, что  , а функция Гамильтона имеет вид
, а функция Гамильтона имеет вид
 .
.
Тогда сопряженная система имеет вид
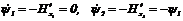 ,
,
и общее решение выписывается в явном виде
 ,
,
где C, D – постоянные.
Исходя из условия максимума функции Гамильтона по управлению, оптимальное управление имеет вид

Таким образом, оптимальное управление u может принимать лишь два значения  и имеет, в силу линейности функции
и имеет, в силу линейности функции  , не более одной точки переключения, т.е. такую точку, в которой функция u меняет знак.
, не более одной точки переключения, т.е. такую точку, в которой функция u меняет знак.
Пусть для определенности 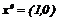 . Очевидно, что управления
. Очевидно, что управления 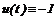 ,
, 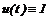 ,
,
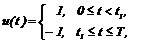
не могут перевести точку из положения (1,0) в начало координат.
Поэтому

Такому управлению и начальным условиям 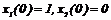 соответствует траектория
соответствует траектория


Из условия 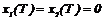 находим
находим 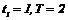 .
.
Таким образом, принцип максимума позволил выделить единственное управление

Это и есть оптимальное управление, поскольку из физических соображений ясно, что решение исходной задачи существует. Следовательно, оптимальна и соответствующая траектория
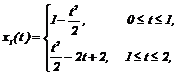
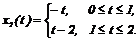
Рассмотрим теперь ту же задачу при всевозможных 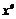 . Сделанный выше вывод о том, что оптимальное управление является кусочно-постоянной функцией, принимающей значения
. Сделанный выше вывод о том, что оптимальное управление является кусочно-постоянной функцией, принимающей значения  и имеющей не более одного переключения, справедлив, при любом
и имеющей не более одного переключения, справедлив, при любом 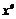 .
.
Для отрезка времени, на котором  , в силу (2.14) имеем
, в силу (2.14) имеем
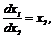
откуда
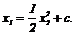
Аналогично при 
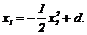
Семейства соответствующих парабол изображены на рис. 2.1.
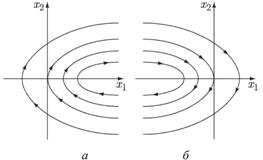
Рис.2.1. Фазовые траектории системы (2.14): а) при u =1; б) при u =-1.
Нетрудно видеть (рис. 2.2), что при любом 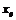 оптимальная фазовая траектория состоит из двух кусков парабол, примыкающих друг к другу (если точка
оптимальная фазовая траектория состоит из двух кусков парабол, примыкающих друг к другу (если точка 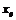 лежит на дуге АО параболы
лежит на дуге АО параболы  или на дуге ВО параболы
или на дуге ВО параболы 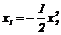 , то первый из кусков парабол, составляющих оптимальную траекторию, вырождается в точку). На рис. 2.3 изображено все семейство таких траекторий.
, то первый из кусков парабол, составляющих оптимальную траекторию, вырождается в точку). На рис. 2.3 изображено все семейство таких траекторий.

Рис. 2.2. Оптимальные фазовые траектории при различных расположениях начальной точки
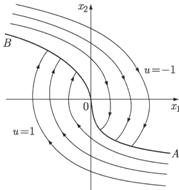
Рис.2.3. Синтез оптимальных управлений
Полученные результаты позволяют задать оптимальное управление как функцию фазовых координат управляемого объекта:

Такая функция v называется синтезирующей функцией, а задача построения синтезирующей функции – задачей синтеза оптимальных управлений. Управление, заданное как функция времени, называется иногда программным управлением.






