Пусть движение управляемого объекта описывается системой дифференциальных уравнений
, (2.1)
где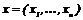 
– вектор координат объекта или фазовых координат, 
– заданная вектор-функция, 
– вектор управлений или просто управление. В уравнении (2.1) векторы x, u являются функциями переменной t, обозначающей время, причем 
, где 
– отрезок времени, на котором происходит управление системой.
На управление обычно накладывается условие
, (2.2)
где 
– заданное множество в 
при каждом .
Будем называть далее управлением кусочно-непрерывную на отрезке (т.е. имеющую конечное число разрывов первого рода) r -мерную вектор-функцию u, непрерывную справа в точках разрыва и непрерывную в точке T. Управление называется допустимым, если оно удовлетворяет ограничению (2.2).
Заметим, что ограничиться рассмотрением непрерывных управлений оказывается невозможным, так как с их помощью трудно моделировать моменты переключения управления такие, как, например, включение и отключение двигателей, отделение ступеней ракеты, поворот рулей и т.д.
Иногда рассматривают и более широкие классы допустимых управлений, например, класс всех ограниченных измеримых управлений, удовлетворяющих условию (2.2).
Покажем, как при произвольном начальном положении 
и допустимом управлении u определяется траектория управляемого объекта. Рассмотрим задачу Коши
. (2.3)
Поскольку при разрывных правых частях классическое понятие решения системы дифференциальных уравнений неприменимо, поясним, что понимается в данном случае под решением задачи (2.3). Для этого поступим следующим образом.
Пусть функция u имеет скачки в точках 
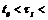
. Предположим, что задача (2.3) имеет решение x, определенное на всем отрезке 
, причем 
. Далее рассмотрим задачу Коши
.
Предполагая, что она имеет решение на отрезке 
и 
, приходим к задаче
.
и т.д.
Если функцию x удалось определить указанным способом на всем отрезке , то будем называть ее решением задачи (2.3) или фазовой траекторией, соответствующей управлению u. Отметим, что x – непрерывная по построению функция, удовлетворяющая на отрезке равенству
.
При выполнении определенных условий на f решение задачи (2.3), соответствующее управлению u, существует и единственно при произвольном начальном положении x 0 и произвольном управлении u. Пример таких условий дает следующая теорема.
Теорема. Пусть вектор-функция f определена и непрерывна по совокупности аргументов на 
и удовлетворяет условию Липшица по x с некоторой константой M >0:
,
.
Тогда при любом и любом кусочно-непрерывном управлении u задача (2.3) имеет единственное решение, определенное на всем отрезке .
Доказательство теоремы, а также более общие факты, касающиеся решения дифференциальных уравнений с разрывными правыми частями, можно найти, например, в [5].
Помимо ограничений на управление могут существовать ограничения и на фазовые координаты
. (2.4)
Ограничения на концах траектории целесообразно рассматривать отдельно:
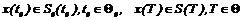; (2.5)
здесь 
– заданные множества из Rn; 
– заданные множества из R, причем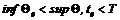 
. Таким образом, начальный и конечный моменты времени не обязательно фиксированы. Случаю фиксированных 
соответствуют множества , состоящие из одной точки; при этом говорят, что рассматривается задача с закрепленным временем.
Если 
при любом 
, то левый конец траектории называют закрепленным. Если же 
при всех , то левый конец траектории называют свободным. Во всех остальных случаях левый конец называют подвижным. В аналогичных ситуациях говорят о закрепленном, свободном или подвижном правом конце траектории.
Цель управления в задаче оптимального управления состоит в минимизации некоторого функционала. Мы будем рассматривать задачу с целевым функционалом
, (2.6)
представляющим собой сумму интегрального функционала 
и терминального функционала 
. Эта задача называется задачей Больца. Ее частными случаями являются задача с интегральным функционалом, называемая задачей Лагранжа, и задачей с терминальным функционалом, называемая задачей Майера. Задача с интегральным функционалом при 
называется задачей оптимального быстродействия.
Задача оптимального управления заключается в минимизации функционала (2.6) на множестве наборов 
таких, что 
, управление u допустимо, траектория x определяется в результате решения задачи Коши (2.3), причем 
и выполнены условия (2.4).
Набор минимизирующий функционал (2.6), называется решением задачи оптимального управления, управление u – оптимальным управлением, а траектория x – оптимальной траекторией. Часто решением задачи оптимального управления называют пару 
.
