Задание по темам 2.1 – 2.5
1. Дана модель объекта управления 
с краевыми условиями x(0) = 1, x(3) = 1, и функционал
J(u, x) = –  ,
,
Требуется найти оптимальную пару  .
.
2. Дана модель объекта управления 
с начальным условием x(0) = 0, и функционал
J(u, x) =  ,
,
Требуется найти оптимальное управление и оптимальную траекторию  .
.
3. Даны модель объекта управления

с начальными условиями  и функционал
и функционал
J(u, x) =  ,
,
Требуется найти оптимальное программное управление и соответствующую ему траекторию  .
.
4. Дана модель объекта управления 
с начальным условием x(0) = 1, и функционал
J(u, x) =  ,
,
Требуется найти оптимальное управление и соответствующую ему оптимальную траекторию  .
.
5. Дана модель объекта управления 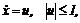
с начальным условием x(0) = 0, и функционал
J(u, x) =  ,
,
Требуется найти оптимальное управление и соответствующую ему оптимальную траекторию  .
.
6. Дана модель объекта управления 
с начальным условием x(0) = 1, и функционал
J(u, x) =  ,
,
Требуется найти оптимальное управление и соответствующую ему оптимальную траекторию  .
.
7. Дана модель объекта управления 
с краевыми условиями x(0) = 1, и функционал
J(u, x) = – 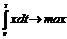 ,
,
Требуется найти оптимальную пару  .
.
8. Дана модель объекта управления 
с начальным условием x(0) = 0, и функционал
J(u, x) =  ,
,
Требуется найти оптимальное управление и оптимальную траекторию  .
.
9. Даны модель объекта управления

с начальными условиями  и функционал
и функционал
J(u, x) =  ,
,
Требуется найти оптимальное программное управление и соответствующую ему траекторию  .
.
10. Дана модель объекта управления 
с начальным условием x(0) = 1, и функционал
J(u, x) =  ,
,
Требуется найти оптимальное управление и соответствующую ему оптимальную траекторию  .
.
11. Дана модель объекта управления 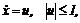
с начальным условием x(0) = 1, и функционал
J(u, x) =  ,
,
Требуется найти оптимальное управление и соответствующую ему оптимальную траекторию  .
.
12. Дана модель объекта управления 
с начальным условием x(0) = 1, и функционал
J(u, x) =  ,
,
Требуется найти оптимальное управление и соответствующую ему оптимальную траекторию  .
.
13. Дана модель объекта управления, начальное условие, функционал

Требуется найти оптимальное управление и соответствующую ему оптимальную траекторию  .
.
14. Дана модель объекта управления, начальное условие, функционал

Требуется найти оптимальное управление и соответствующую ему оптимальную траекторию  .
.
15. Дана модель объекта управления, начальное условие, функционал

Требуется найти оптимальное управление и соответствующую ему оптимальную траекторию  .
.
16. Дана модель объекта управления, начальное условие, функционал

Требуется найти оптимальное управление и соответствующую ему оптимальную траекторию  .
.
17. Дана модель объекта управления, начальное условие, функционал
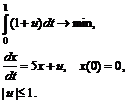
Требуется найти оптимальное управление и соответствующую ему оптимальную траекторию  .
.
18. Дана модель объекта управления, начальное условие, функционал

Требуется найти оптимальное управление и соответствующую ему оптимальную траекторию  .
.
19. Дана модель объекта управления, начальное условие, функционал

Требуется найти оптимальное управление и соответствующую ему оптимальную траекторию  .
.
20. Дана модель объекта управления, начальное условие, функционал

Требуется найти оптимальное управление и соответствующую ему оптимальную траекторию  .
.
21. Дана модель объекта управления с начальным условием и функционал


Требуется найти оптимальное управление и соответствующую ему оптимальную траекторию  .
.
22. Дана модель объекта управления с начальным условием и функционал

Требуется найти оптимальное управление и соответствующую ему оптимальную траекторию  .
.
23. Дана модель объекта управления с начальным условием и функционал

Требуется найти оптимальное управление и соответствующую ему оптимальную траекторию  .
.
24. Дана модель объекта управления с начальным условием и функционал

Требуется найти оптимальное управление и соответствующую ему оптимальную траекторию  .
.
25. Дана модель объекта управления с начальным условием и функционал

Требуется найти оптимальное управление и соответствующую ему оптимальную траекторию  .
.
Задание по темам 2.6 – 2.8
Решить задачу оптимального накопления капитала от начального значения K(0)=K0 до конечного значения K(T)=KT за фиксированное время T.
Уравнение накопления капитала имеет вид

где  - производственная функция Коба-Дугласа,
- производственная функция Коба-Дугласа,
K – капиталовложения,
L – трудозатраты.
В качестве критерия оптимальности использовать минимизацию функционала
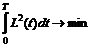
с учетом ограничений на трудозатраты 
| № | K0 | KT | T | 
| 
| L max | 
|
| 1. | 1 | 3 | 10 | 0.3 | 0.2 | 5 | 1.002 0.53 0.46 |
| 2. | 2 | 5 | 7 | 0.7 | 0.4 | 3 | 1.002 0.21 0.78 |
| 3. | 1 | 5 | 10 | 0.5 | 0.2 | 5 | 1.2 0.37 0.59 |
| 4. | 3 | 10 | 5 | 0.8 | 0.8 | 7 | 1.4 0.3 0.7 |
| 5. | 2 | 8 | 10 | 0.9 | 0.4 | 5 | 1.1 0.4 0.68 |
| 6. | 3 | 8 | 5 | 0.4 | 0.2 | 6 | 1.23 0.56 0.42 |
| 7. | 5 | 15 | 10 | 0.5 | 0.4 | 5 | 1.08 0.32 0.44 |
| 8. | 3 | 10 | 8 | 0.7 | 0.3 | 8 | 1.7 0.4 0.6 |
| 9. | 2 | 15 | 10 | 0.8 | 0.5 | 10 | 1.2 0.33 0.66 |
| 10. | 1 | 3 | 6 | 0.9 | 0.6 | 6 | 2.1 0.32 0.59 |
| 11. | 3 | 8 | 10 | 0.6 | 0.2 | 6 | 1.23 0.56 0.43 |
| 12. | 2 | 10 | 8 | 0.9 | 0.4 | 5 | 1.1 0.4 0.68 |
| 13. | 1 | 5 | 8 | 0.5 | 0.3 | 4 | 1.2 0.37 0.59 |
| 14. | 5 | 10 | 5 | 0.5 | 0.1 | 7 | 1.4 0.3 0.7 |
| 15. | 2 | 5 | 10 | 0.5 | 0.2 | 5 | 1.2 0.37 0.59 |
| 16. | 3 | 8 | 3 | 0.8 | 0.5 | 5 | 1.4 0.3 0.7 |
| 17. | 2 | 6 | 10 | 0.8 | 0.4 | 5 | 1.1 0.4 0.68 |
| 18. | 3 | 9 | 5 | 0.4 | 0.1 | 4 | 1.23 0.56 0.42 |
| 19. | 1 | 10 | 15 | 0.7 | 0.3 | 8 | 1.7 0.4 0.6 |
| 20. | 5 | 15 | 7 | 0.8 | 0.4 | 8 | 1.2 0.33 0.66 |
| 21. | 1 | 5 | 6 | 0.9 | 0.4 | 6 | 2.1 0.32 0.59 |
| 22. | 2 | 10 | 20 | 0.6 | 0.2 | 6 | 1.23 0.56 0.43 |
| 23. | 3 | 10 | 8 | 0.7 | 0.4 | 8 | 1.7 0.4 0.6 |
| 24. | 2 | 10 | 8 | 0.8 | 0.3 | 9 | 1.2 0.33 0.66 |
| 25. | 1 | 4 | 7 | 0.9 | 0.4 | 6 | 2.1 0.32 0.59 |






