Исследуем на экстремум функционал
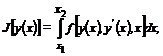(1.13)
где 
непрерывная и трижды дифференцируемая функция своих аргументов.
Искомая функция, для которой этот функционал принимает экстремальное значение, удовлетворяет краевым условиям
y (x 1) = у 1; y (x 2) = у 2. (1.14)
Задача о нахождении экстремума функционала (1.13) при условиях (1.14) называется вариационной задачей с закрепленными граничными точками.
Подчеркнем, что целью исследования является также и нахождение функции y (x), доставляющей экстремум функционалу (1.13).
Непрерывно дифференцируемые функции y (x), определенные на [ x 1, x 2] и удовлетворяющие условиям (1.14), называются допустимыми функциями.
Будем искать такую кривую у = y (x) на участке x 1< x < x 2, которая реализует экстремум функционала 
.
Примем, что решение найдено и соответствует функции y (x) = y о(x). Рассмотрим однопараметрическое семейство кривых y 1(x) и y 2(x). Уравнение, описывающее семейство кривых (допустимые функции), можно представить в виде
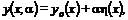
где η(х) – произвольная функция, обращающаяся в нуль на x = x 1 и x = x 2; α – параметр. Каждой кривой будут соответствовать свои значения (числа) α, а значениям α = 0 будет соответствовать кривая y о(x), доставляющая экстремум функционалу.
Первая вариация функционала будет
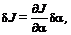
необходимое условие экстремума
d J = 0.
Запишем функционал в виде
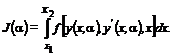
Произведем дифференцирование под знаком интеграла
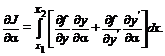(1.15)
Второй интеграл представим в виде
(1.16)
и вычислим его по частям.
Если обозначить 
, то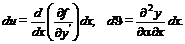 
С учетом введенных обозначений выражение (1.16) запишем в виде
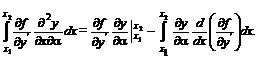
Учитывая, что кривые семейства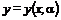 
проходят через точки x 1, y 1 и x 2, y 2, можно записать
, а функция η (х) выбрана так, что η (х 1) = 0 и η (х 2) = 0.
Теперь выражение (1.15) можно записать в виде
или, учитывая, что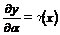 
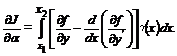
Тогда для вариации функционала имеем
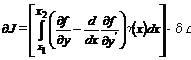
Если учесть, что 
, то необходимое условие экстремума функционала будет
(1.17)
К выражению (1.17) применим лемму Лагранжа. Тогда вместо (1.17) запишем выражение, которое называется уравнением Эйлера
Экстремум функционала J будет достигаться только для таких кривых y (x), которые удовлетворяют дифференциальному уравнению Эйлера.
Кривые, соответствующие решению уравнения Эйлера y = y (x, С1, С2), где С1 и С2 – произвольные постоянные, называются экстремалями.
Для удобства записи введем принятые в вариационном исчислении условные обозначения
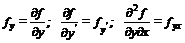и т. д.
В этом случае уравнение Эйлера примет вид
Пример. Найти экстремали функционала
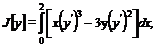
при граничных условиях y (0) = 4, y (2) = 6.
Решение.
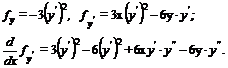
Уравнение Эйлера
Решение второе входит в семейство первых. С1 и С2 находим из граничных условий.
С2 = 4;
2С1 + 4 = 6;
С1 = 1.
Таким образом, экстремаль y = х +4.
Уравнение Эйлера не всегда интегрируется в квадратурах, поэтому важно рассмотреть частные случаи, когда такое интегрирование возможно.
1. Интегрант не зависит от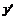 
В этом случае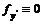 
и уравнение Эйлера имеет вид f у = 0, т. е. является алгебраическим уравнением.
2. Интегрант линейно зависит от .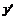
Этот случай охватывает предыдущий и соответствует функциям, для которых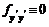 
, т. е. f = f (x, y) или f = m (x, y) + 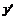n (x, y). Такие функционалы называются вырожденными.
3. Интегрант зависит только от .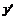
В этом случае уравнение Эйлера: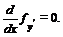 
Видно, что первый интеграл будет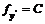 
, т. е. алгебраическое уравнение относительно 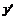и все его решения можно представить в виде 
, а экстремалями являются семейства функций y = С 1 + С 2 х с произвольными постоянными, определяемыми из краевых условий.
4. Интегрант не зависит от у, т. е. может зависеть от 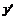и х (если не зависит и от х, то это предыдущий случай). Уравнение Эйлера 
и, следовательно, 
.
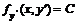Это или дифференциальное уравнение первого порядка, или алгебраическое.
5. Интегрант не зависит явно от х
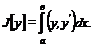
Если функционал не вырожденный, т. е.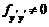 
, то уравнение Эйлера сводится к следующему
Условие Лежандра
Предположим, что экстремаль найдена и первая вариация обращается в нуль. Тогда при достаточно малом параметре α члены высшего порядка малости в полном приращении функционала убывают быстрее, чем квадратичный член.
В этом случае знак полного приращения функционала 
совпадает со знаком второй вариации
Вследствие этого, для того чтобы y (х) доставляла min функционалу, необходимо выполнение условия
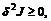
для max соответственно
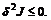
Условия Лежандра будут иметь вид:
при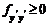 
имеем на экстремали min J,
при 
имеем на экстремали max J.
