ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ И
МЕТОДЫ ОПТИМИЗАЦИИ
Учебное пособие
для студентов, обучающихся по направлениям
010302 – Прикладная математика и информатика,
010402 – Прикладная математика и информатика,
020303 – Математическое обеспечение и
администрирование информационных систем
Стерлитамак
2016
УДК 517.9
ББК 22.18
М 91
Рецензенты:
доктор технических наук, профессор Е.А. Муравьева (Стерлитамакский филиал Уфимского государственного нефтяного технического университета); доктор физико-математических наук, профессор Михайлов П.Н. (Стерлитамакский филиал Башкирского государственного университета); кафедра естественнонаучных и общепрофессиональных дисциплин (Уфимский государственный авиационный технический университет филиал в г. Стерлитамак); кафедра математического моделирования (Стерлитамакский филиал Башкирского государственного университета)
Ответственный редактор – доктор физико-математических наук, профессор С.А. Мустафина (Стерлитамакский филиал Башкирского государственного университета)
| М 91 | Мустафина С.А., Карамова А.И. Вариационное исчисление и методы оптимизации: Учебное пособие. – Стерлитамак: Стерлитамакский филиал БашГУ, 2016. – 92 с. |
Учебное пособие содержит основные теоретические сведения разделов вариационного исчисления, оптимального управления и динамического программирования. В пособии приводятся решения тестовых примеров по каждой теме, варианты контрольных заданий и задачи для самостоятельного решения.
Предназначается для студентов старших курсов дневного и заочного отделений, магистрантов, аспирантов физико-математического факультета.
УДК 517.9
ББК 22.18
М 91
© Мустафина С.А., Карамова А.И., 2016
© Стерлитамакский филиал БашГУ, 2016
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ.. 4
1. ОСНОВНЫЕ ПОНЯТИЯ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ.. 6
1.1. Основные определения. 8
1.2. Вариация функционала. 11
1.3. Условия экстремума функционала. 12
1.4. Уравнение Эйлера (простейшая вариационная задача) 13
1.5. Условие Лежандра. 18
1.6. Функционалы от нескольких функций. 18
1.7. Функционалы, зависящие от производных высших порядков. 19
1.8. Каноническая форма уравнений Эйлера. 20
1.9. Функционалы, зависящие от функций нескольких переменных. 21
1.10. Задачи на условный экстремум.. 24
1.11. Изопериметрическая задача. 26
Задания для самостоятельной работы.. 27
2. ЭЛЕМЕНТЫ ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ.. 32
2.1. Постановка задачи оптимального управления. 32
2.2. Принцип максимума Понтрягина. 35
2.3. Алгоритм применения принципа максимума. 38
2.4. Решение задач вариационного исчисления. 43
2.5. Примеры решение задач на принцип максимума. 44
2.6. Задача с фиксированными концами (увеличение капитала до заданного значения) 48
2.7. Задача со свободным правом концом.. 51
(максимизация потребления) 51
2.8. Задача с подвижным правым концом.. 53
Задания для самостоятельной работы.. 56
3. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ.. 65
3.1. Постановка задачи динамического программирования. 65
3.2. Примеры задач динамического программирования. 71
3.3. Задача о загрузке рюкзака (задача о ранце) 74
Задания для самостоятельной работы.. 82
БИБЛИОГРАФИЧЕСКИЙ СПИСОК.. 90
ВВЕДЕНИЕ
В жизни постоянно приходится сталкиваться с необходимостью принять наилучшее возможное (иногда говорят – оптимальное) решение. Огромное число подобных проблем возникает в экономике и технике. При этом часто случается так, что полезно прибегнуть к математике.
В математике исследование задач на экстремум (т. е. на максимум и минимум) началось давно – двадцать пять веков назад. Долгое время к задачам на отыскание экстремумов не было сколько-нибудь единых подходов. Но примерно триста лет назад – в эпоху формирования математического анализа – были созданы первые общие методы решения и исследования задач на экстремум. Тогда же выяснилось, что некоторые специальные задачи оптимизации играют очень важную роль в естествознании, а именно обнаружилось, что многие законы природы допускают вывод из так называемых «вариационных принципов», согласно которым истинное движение механической системы, света, электричества, жидкости, газа и т. п. можно выделить из произвольной совокупности допустимых движений тем, что они минимизируют или максимизируют некоторые величины. В конце XVII столетия было поставлено несколько конкретных экстремальных задач естественнонаучного содержания (брахистохрона, задача Ньютона и др.). Потребность решать как их, так и многие другие проблемы, возникающие в геометрии, физике, механике, привела к созданию новой главы математического анализа, получившей название вариационного исчисления.
Интенсивное развитие вариационного исчисления продолжалось около двух столетий. В нем принимали участие многие замечательные ученые XVIII и XIX веков, и к началу XX столетия стало казаться, что они почти исчерпали эту тематику. Но это оказалось не так. Потребности практической жизни, особенно в области экономики и техники, в последнее время выдвинули такие новые задачи, которые старыми методами решить не удавалось. Надо было идти дальше. Пришлось несколько развить математический анализ и создать новый его раздел — «выпуклый анализ», где изучались выпуклые функции и выпуклые экстремальные задачи. С другой стороны, потребности техники, в частности космической, выдвинули серию задач, которые также не поддавались средствам вариационного исчисления. Необходимость решать их привела к созданию новой теории, получившей название теории оптимального управления. Основной метод в теории оптимального управления был разработан в 1950—60-е годы нашими соотечественниками – Л. С. Понтрягиным и его учениками. Это привело к тому, что теория экстремальных задач получила новый мощный толчок к дальнейшим исследованиям.
Опыт преподавания показывает, что раздел вариационного исчисления и оптимального управления – один из наиболее сложных для освоения. Это, прежде всего, связано с концептуальными отличиями изучаемых в нем задач оптимального управления от задач конечномерной оптимизации, и, как следствие, с существенным усложнением используемых в них условий оптимальности. В связи с этим представляется полезным дать наглядную иллюстрацию применения данных условий оптимальности к решению задач различных типов. Настоящее пособие и является попыткой дать такую иллюстрацию. В нем содержатся примеры и задачи по трем темам:
· вариационному исчислению;
· принципу максимума;
· динамическому программированию.
Каждый раздел состоит из теоретической части, описывающей базовые понятия и результаты, используемые при решении соответствующих задач, примеров с решениями, а также задач для самостоятельной работы студентов.
Следует подчеркнуть, что данное пособие ни в коем случае не является теоретическим курсом, а ориентировано, прежде всего, на практическое применение методов оптимального управления. По мнению авторов-составителей, данное пособие будет полезным преподавателям при подготовке и проведении практических занятий по разделу "Вариационное исчисление и оптимальное управление", а также студентам при выполнении домашних заданий по этой теме.
ОСНОВНЫЕ ПОНЯТИЯ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
Курс вариационного исчисления является продолжением дифференциального и интегрального исчислений и в нем изучаются разнообразные экстремальные задачи. Многие важнейшие уравнения механики (динамики, теории упругости и т. д.) получены именно как решение экстремальных задач.
Необходимо также отметить, что классическое вариационное исчисление является базой для решения задач оптимального управления и фундаментальной основой современных методов оптимального управления, таких как принцип максимума Понтрягина, динамическое программирование и т. д.
Примеры решения экстремальных задач известны даже из древней истории. Известна так называемая задача Дидоны. В IX в. до н. э. финикийская царевна Дидона со спутниками бежала из г. Тира и высадилась на африканском берегу Средиземного моря. Хитрая Дидона упросила местных жителей отдать ей участок земли, который можно охватить шкурой быка. Простодушный правитель не понял глубины проблемы, а Дидона разрезала шкуру на тончайшие полоски и получившейся веревкой охватила достаточно большую площадь, на которой был заложен Карфаген. Если длина веревки L, то требуется найти такую форму кривой, которая охватывает наибольшую площадь. В формальной постановке будем считать, что кривая у (х) гладкая, т. е. непрерывно дифференцируема, и определена на отрезке [ a, в ], при этом у (а) = у (в) = 0. Длина кривой, как это известно, из интегрального исчисления, определяется по формуле
 (1.1)
(1.1)
 (1.2)
(1.2)
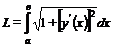 . (1.3)
. (1.3)
Площадь S определяется интегралом
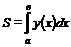 . (1.4)
. (1.4)
Экстремальная задача здесь следующая: найти такую гладкую функцию у (х), которая удовлетворяет условиям (1.1) и (1.2) при заданном L и обеспечивает интегралу (1.4) максимальное значение.
Подобные задачи ставили и решали еще Аристотель и Архимед, однако считается, что вариационное исчисление как математическая дисциплина оформилась в 1696 г., когда И. Бернулли предложил задачу, решение которой независимо нашли Я. Бернулли, Лопиталь и И. Ньютон. Это задача о брахистрохроне. В вертикальной плоскости через две заданные точки О и В, не лежащие на одной вертикали, провести кривую (т. е. найти её уравнение), двигаясь по которой материальная точка под действием силы тяжести пройдет от точки О до В за наименьшее время.
В силу теоремы о сохранении энергии, если скорость точки в точке О равна 0, можно записать
 . (1.5)
. (1.5)
Откуда  . Так как
. Так как
 (1.6)
(1.6)
где ds – дифференциал дуги, то
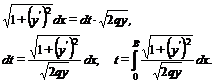 (1.7)
(1.7)
Таким образом, нужно найти гладкую функцию у (х), для которой  при краевых условиях у (0) = 0, у(в) = уВ. Задача усложняется, если кривую ищем не до точки В, а до известной кривой φ(t) или если необходимо найти линию наискорейшего спуска между двумя известными линиями φ(t) и ψ(t).
при краевых условиях у (0) = 0, у(в) = уВ. Задача усложняется, если кривую ищем не до точки В, а до известной кривой φ(t) или если необходимо найти линию наискорейшего спуска между двумя известными линиями φ(t) и ψ(t).
В этих вариационных задачах необходимо найти не только форму кривой, но и координаты начала и конца линии.
Большой класс задач, приводящих к вариационным проблемам, связан с оптимальным управлением. Например, задача поворота вала двигателя на заданный угол без остановки (с остановкой) за минимальное время с ограничением на управление (без этого ограничения задача становится бессмысленной). Часто ставится также вариационная задача поворота вала двигателя на заданный угол за заданное время Т при минимальном расходе энергии.
Много задач связано с управлением летательных аппаратов, например ракет. Проблема вывода ракеты в заданную точку фазового пространства (координаты и скорости) за минимальное время при ограничении на величину реактивной силы  . Или, например, задача перевода летательного аппарата на максимальную дальность или высоту, т. е. при заданных уравнениях объекта, фазовых ограничениях, ограничениях на управление (запас топлива ограничен и известно ограничение на максимальную силу тяги) и заданных краевых условиях. Таким образом, необходимо найти управление, обеспечивающее максимальную дальность или высоту.
. Или, например, задача перевода летательного аппарата на максимальную дальность или высоту, т. е. при заданных уравнениях объекта, фазовых ограничениях, ограничениях на управление (запас топлива ограничен и известно ограничение на максимальную силу тяги) и заданных краевых условиях. Таким образом, необходимо найти управление, обеспечивающее максимальную дальность или высоту.
К вариационным задачам приводят также проблемы обработки информации, выделение полезного сигнала на фоне помех и т. д.
Примеров постановок вариационных задач можно приводить много, но из изложенного выше следует, что изучение курса «Вариационное исчисление и оптимальное управление» должно обеспечить:
- понимание постановки вариационных задач;
- умение ставить вариационную задачу;
- умение находить решение вариационных задач в рамках классического вариационного исчисления.
Основные определения
Одним из базовых понятий вариационного исчисления является понятие функционала.
ОПРЕДЕЛЕНИЕ. Переменная величина J [ у (х)] называется функционалом, зависящим от функции у (х), если каждой функции у (х) для некоторого класса функций соответствует число J.
Аналогично определяются функционалы, зависящие от нескольких функций. Можно считать, что функционал представляет собой обобщение понятия функции, в котором роль независимой переменной играет другая функция. Еще раз подчеркнём, что значением функционала является число.
Довольно часто придется иметь дело с функционалами вида
 (1.8)
(1.8)
При формулировке понятия функционала использовано выражение «некоторый класс функций», вследствие чего необходимо расшифровать это выражение и рассмотреть функциональные пространства.
При изучении функций n -переменных удобно пользоваться геометрическим языком, рассматривая набор n чисел (у 1, у 2, …, у n) как точку n -мерного пространства.
При изучении функционалов каждую функцию у (х), принадлежащую какому-либо классу, будем рассматривать как точку некоторого пространства.
ОПРЕДЕЛЕНИЕ. Пространства, элементами которых являются функции, называются функциональными пространствами.
Для исследования функционалов необходимо ввести для функций понятие нормы – аналога расстояния между точками в евклидовом пространстве.
Сформулируем определение линейного нормированного пространства.
ОПРЕДЕЛЕНИЕ. Линейное пространство – совокупность R элементов х, у, z … произвольной природы, для которых определены операции сложения и умножения их на числа, причем выполнены следующие аксиомы:
1. х + у = у + х.
2. (х + у) + z = х + (у + z).
3. Существует такой нулевой элемент 0, что х + 0 = х.
4. Для каждого 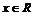 существует такой элемент (- х), что х +(- х) = 0.
существует такой элемент (- х), что х +(- х) = 0.
5. 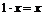
6. 
7. 
8. 
ОПРЕДЕЛЕНИЕ. Линейное пространство будет нормированным, если каждому элементу 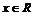 поставлено в соответствие неотрицательное число || x || – норма этого элемента, так что
поставлено в соответствие неотрицательное число || x || – норма этого элемента, так что
1. || x || = 0 при х = 0.
2. 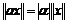 .
.
3. || x + y ||  || x || + || y ||.
|| x || + || y ||.
В линейном нормированном пространстве можно рассматривать расстояние между элементами, понимая под расстоянием между х и у величину || x - у ||.
Представляют особый интерес следующие пространства.
Пространство С, состоящее из всех непрерывных функций с нормой || у ||с = max | y (x)|, a < x < b.
Пространство С 1 функций с нормой
 . (1.9)
. (1.9)
Гильбертово пространство L 2 функций, суммируемых с квадратом на отрезке [ a, в ] и с нормой
 (1.10)
(1.10)
ОПРЕДЕЛЕНИЕ. Если функционал J (y) задан на линейном пространстве L и представляет собой линейную форму, т. е.
 (1.11)
(1.11)
то функционал называется линейным.
При изучении функционалов вводят ряд понятий, аналогичных понятиям для функций: непрерывность, дифференцируемость, экстремум и др.
ОПРЕДЕЛЕНИЕ. Функционал J [ y (x)], определенный на нормированном пространстве М, называют непрерывным в точке  , если для всякого числа
, если для всякого числа  существует такая
существует такая  окрестность точки у о, что для любой точки у из этой окрестности выполнено неравенство
окрестность точки у о, что для любой точки у из этой окрестности выполнено неравенство
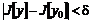
ОПРЕДЕЛЕНИЕ. Разность у (х) – у о(х) = δ у (х) называется вариацией функции у о(х).
Необходимо подчеркнуть отличие понятия вариации от приращения функции в точке.
Приращение функции в точке х о – число, равное разности двух значений функций, а вариация – это функция, равная разности двух функций, являющихся аргументами функционала.
Вариация функционала
ОПРЕДЕЛЕНИЕ. Функционалы, заданные с помощью интегралов, называются интегральными функционалами, а подынтегральная функция интегрантом.
Пусть  Где у (х) трижды дифференцируемая функция. Приращение функционала, соответствующее приращению аргумента δ у (х) (полное приращение функционала), можно записать в виде
Где у (х) трижды дифференцируемая функция. Приращение функционала, соответствующее приращению аргумента δ у (х) (полное приращение функционала), можно записать в виде
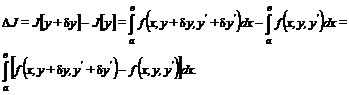 (1.12)
(1.12)
Применим к подынтегральной функции формулы Тейлора

где 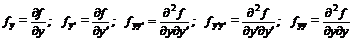
(обозначения производных, принятые в вариационном исчислении).
Отметим, что вторые производные взяты в точке (х, у (х), у’ (х)).
Первое слагаемое (линейная часть) и есть первая вариация

вторая вариация

где ε члены в разложении, порядок которых больше чем два.






