Символическим методом расчета установившихся режимов в линейных цепях синусоидального тока называют метод, использующий представление синусоидальных функций комплексными числами. Такой переход осуществляется с помощью соотношения Эйлера:
,
где
 и  .
| (2.6) |
Соотношение (2.6) позволяет поставить в соответствие синусоидальной функции комплексное число. Так, для тока, напряжения и ЭДС запишем соответствие между синусоидальными функциями и комплексными числами:
| (2.7) |
где 
– мнимая единица; 
, 
и 
– комплексы действующих значений тока, напряжения и ЭДС.
Такое представление позволяет при определении токов и напряжений в цепи перейти от решения систем уравнений с синусоидальными функциями времени к расчету систем алгебраических линейных уравнений с комплексными коэффициентами. Систему уравнений можно получить как по законам Кирхгофа в комплексном виде, так и любым методом расчета цепей: по закону Ома, методом контурных токов, узловых потенциалов, эквивалентного генератора или эквивалентными преобразованиями цепи. При составлении системы уравнений используются схемы замещения цепи в комплексном виде.
Законы Кирхгофа в комплексной форме
1. Алгебраическая сумма комплексных значений токов в проводниках, соединенных в узел, равна нулю:
| (2.8) |
2. Алгебраическая сумма комплексных значений напряжений на всех сопротивлениях замкнутого контура равна алгебраической сумме комплексных значений ЭДС всех источников того же контура:
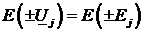
| (2.9) |
Векторные диаграммы
Для иллюстрации взаимосвязи между токами и напряжениями в конкретной схеме строят векторные диаграммы. Различают три вида векторных диаграмм.
| Исходный элемент | Схема замещения | Векторная диаграмма |
Источники ЭДС
|
| 
|
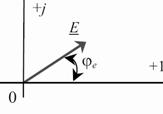
Резистор
|
| 
|
Емкость
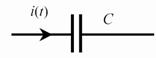
 – емкостное сопротивление (Ом)
| 
| 
|
Индуктивность
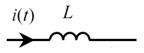
 – индуктивное сопротивление (Ом)
|
| 
|
Векторная диаграмма токов – представляет собой сумму векторов токов на комплексной плоскости, соответствующую первому закону Кирхгофа, записанному для определенного узла цепи.
Векторная диаграмма напряжений – это сумма векторов напряжений на комплексной плоскости, построенная в соответствии со вторым законом Кирхгофа.
Топографическая диаграмма – является диаграммой комплексных потенциалов цепи на комплексной плоскости, причем один из потенциалов принимается равным нулю, а остальные потенциалы определяются через падения напряжения на элементах цепи.
При построении диаграмм должны быть заданы масштабы напряжений, потенциалов и токов, тогда длина векторов напряжений и токов будет пропорциональна их действующим значениям, а угол поворота векторов относительно вещественной оси равен их начальной фазе. Положительные значения углов отсчитываются против направления вращения часовой стрелки, а отрицательных - по часовой стрелке.
Элементы линейной цепи гармонического тока, их схемы замещения и векторные диаграммы приведены в табл. 2.1.
• Закон Ома в комплексной форме, треугольники сопротивлений и проводимостей
Рис. 2.7. Треугольники: а) сопротивлений; б) проводимостей; в) мощностей
Закон Ома в комплексной форме:
 ,
| (2.10) |
где 
– суммарное реактивное сопротивление ветви (рис. 2.7, а); 
– комплексное сопротивление ветви; 
– модуль и 
– ее угол; 
– суммарная комплексная проводимость ветвей, где 
– модуль; 
– угол; 
и 
– активная и реактивная проводимость (рис. 2.7, б).
