Определение параметров эквивалентного генератора ­  и  относительно зажимов заданного резистора

Для определения тока методом эквивалентного генератора вам необходимо вернутся к исходной схеме, построенной в EWB (с двумя источниками), а также с подключенными амперметрами и вольтметрами.

В исходной схеме вашего варианта задания (табл. 1.1) восстановить заданную величину  источника ЭДС.

Установить величину резистора той ветви, в которой вам необходимо найти ток методом эквивалентного генератора равной 50 мОм (соответствует разры­ву в данном месте цепи) и вольтметром, который подключен к резистору исследуемой ветви, измерить величину напря­жения на разомкнутых зажимах сопротивления  (режим хо­лостого хода). Напряжение эквивалентного генератора .

Установить величину резистора величину резистора той ветви, в которой вам необходимо найти ток методом эквивалентного генератора равной  (соответствует корот­кому замыкания в данном месте цепи) и амперметром измерить ве­личину тока 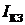 (ток короткого замыкания) в исследуемой ветви.

По результатам моделирования рассчитать значение входного сопротивления .

По известным параметрам эквивалентного генератора  и  рассчитать искомый ток в ветви по формуле , где  - сопротивление ветви, в которой производится расчет тока методом эквивалентного генератора. Результаты измерений и расчета занести в соответствующие графы табл. 1.3.

По результатам расчетов сделать выводы.

 

Содержание отчета

Расчеты контрольных заданий по вариантам.

1. Цель работы.

2. Схема вашего варианта задания

3. Расчеты, выполненные при подготовке к лабораторной работе

4. Исследование линейной цепи методом наложения

4.1 Схема исследуемой цепи с двумя источниками, построенная в EWB (скриншот с показаниями приборов), табл. 1.2

4.2. Схема исследуемой цепи, построенная в EWB, в которой ток  источника тока равен нулю, а значение ЭДС  источника ЭДС имеет исходное значение  (скриншот с показаниями приборов).

4.3. Схема исследуемой цепи, построенная в EWB, в которой значение ЭДС  источника ЭДС равно нулю, а ток  источника тока имеет исходное значение (скриншот с показаниями приборов).

 

 5. Исследование линейной цепи методом узловых потенциалов

5.1  Схемы измерения потенциалов всех пронумерованных узлов в исходной схеме (с двумя источниками), табл. 1.4

5.2. Формулы для расчет токов по измеренным потенциалам

 

6. Опытное определение параметров источника ЭДС.

6.1. Схемы измерения  и 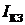 (скриншоты с показаниями приборов).

6.2. Расчетные формулы для определения  и искомого тока в заданной ветви.

7. Анализ полученных результатов и выводы по лабораторной работе.

 

Контрольные вопросы и задания

1. Какие элементы содержит электрическая цепь и для чего эти элементы предназначены?

Как строится схема замещения электрической цепи?

Изложите основные сведения об источниках напряжения и тока и их эквивалентности?

4. Нарисуйте внешние характеристики идеальных источников на­пряжения и тока.

5. Как записывается закон Ома для ветви с последовательным со­единением ЭДС и резисторов?

Сформулируйте законы Кирхгофа.

Как выбираются знаки у составляющих, которые входят в пер­вый и второй законы Кирхгофа?

8. Сколько уравнений необходимо составить по первому и второму законам Кирхгофа для определения токов в цепи?

9. Изложите суть метода расчета цепей по законам Кирхгофа.

10. Изложите суть метода узловых потенциалов для расчета цепей.

11. Изложите суть метода наложения для расчета цепей.

12. Можно ли при менять принцип наложения для определения на­пряжений на ветвях цепи?

13. Изложите суть метода эквивалентного генератора для расчета цепей.

14. При каком значении сопротивления нагрузки в нем выделяется максимальная мощность?

15. Как экспериментально определить параметры эквивалентного генератора?

16. Как экспериментально определить эквивалентные параметры ис­точников ЭДС и тока?

17. Составить систему уравнений по законам Кирхгофа для схемы рис. 1.10.

Записать закон Ома для предложенной схемы рис. 1.10.

Составить систему уравнений методом контурных токов для предложенной схемы.

20. Составить систему уравнений методом узловых потенциалов для предложенной схемы.

21. Определить входное сопротивление цепи относительно зажимов резистора .

22. Определить входное сопротивление цепи относительно зажимов резистора .

23. Определить входное сопротивление цепи относительно зажимов резистора .

24. Определить напряжение холостого хода относительно зажимов резистора .

25. Определить напряжение холостого хода относительно зажимов резистора .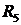

26. Определить напряжение холостого хода относительно зажимов резистора .

 

 

Список литературы

1. Основы теории цепей. Практический курс: [учебное пособие / Б. В. Литвинов и др.]. - Новосибирск, 2011. - 346 с.: ил., схемы
2.  Нейман В. Ю. Теоретические основы электротехники в примерах и задачах. Ч. 1: учебное пособие / В. Ю. Нейман; Новосиб. гос. техн. ун-т, Фак. мехатроники и автоматизации. - Новосибирск, 2008. - 114, [1] с.: ил.. - Режим доступа: http://www.library.nstu.ru/fulltext/metodics/2008/neim.rar
3. Схемотехническое моделирование электрических цепей. Ч. 1: лабораторный практикум для электротехнических специальностей всех форм обучения / Новосиб. гос. техн. ун-т; [сост.: В. А. Аксютин, Ф. Э. Лаппи, В. Ю. Нейман]. - Новосибирск, 2011. - 103 с.: ил., табл.

4. Бессонов Л. А. Теоретические основы электротехники. Электрические цепи: учебник для бакалавров / Л. А. Бессонов. - М., 2012. - 701 с.: ил., табл.

Лабораторная работа

Простейшие линейные цепи

с синусоидальными источниками

Цель работы

Теоретически и с помощью пакета программ E1ectronics Workbench (EWB) исследовать зависимости токов и напряжений в резисторе, ка­тушке индуктивности, конденсаторе при их простейших соединениях в цепи с синусоидальными источниками. Освоить символический метод расчета, проверить справедливость первого и второго законов Кирхгофа.

2.1. Основные теоретические сведения

 

2.1.1. Гармонический ток и его характеристики

В лабораторной работе исследуются линейные электрические цепи с гармоническими источниками, в которых напряжения, ЭДС и токи изменяются по синусоидальному закону и имеют одинаковую частоту (рис. 2.1).

,  и ,

где 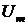, ,  - амплитудные или максимальные значения;  - угловая частота сигнала; 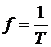 - частота сигнала;  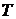- период колебаний; ,  и 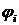 - начальные фазы гармонических колебаний.

Одной из основных характеристик гармонических сигналов являет­ся их среднеквадратичные (действующие) значения:

,  и  .

(2.1)

 

Рис. 2.1. Графики гармонических сигналов ЭДС и тока

 

Электрическая цепь переменного тока кроме источников может со­держать такие элементы, как резисторы, конденсаторы, катушки ин­дуктивности, катушки взаимной индуктивности. Такие элементы цепи называют пассивными. Для расчета элементы цепей представляют их схемами замещения. Каждая такая схема замещения должна учитывать основные электромагнитные процессы, протекающие в конкретном элементе.

 

2.1.2. Резистор

 

В резистивных элементах (или их еще называют активными сопро­тивлениями и обозначают ) электромагнитная энергия необратимо преобразуется в тепло или иные виды энергии. Мгновенная мощность, с которой происходит преобразование энергии, определяется соотношением: .

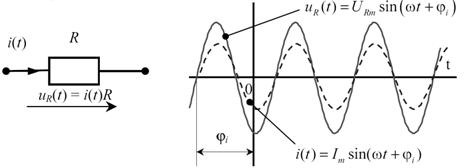
                а)                                                   б)

Рис. 2.2. Гармонический ток и напряжение на резисторе

 

В резистивном элементе (рис. 2.2, а) напряжение связано с током законом Ома . Если ток в резисторе , то напряжение  имеет синусоидальную форму и та­кую же фазу, что и ток в резисторе. Говорят, что ток и напряжение в резисторе совпадают по фазе (рис. 2.2, б).

Средняя мощность, рассеиваемая в резисторе за период, определя­ется соотношением:

 

Катушка индуктивности

Рис. 2.3. Схемы замещения катушки индуктивности

 

Если через катушку индуктивности (рис. 2.3, а) пропустить пере­менный синусоидальный ток , то он создаст пере­менный магнитный поток, пронизывающий витки катушки. По закону электромагнитной индукции на зажимах катушки этот переменный поток наведет синусоидальное напряжение:

,

(2.2)

 

где  - число витков катушки; 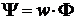 - потокосцепление;  –индуктивность, размерностью Генри (Гн);  – реактивное индук­тивное сопротивление размерностью Ом.

Катушка индуктивности обладает способностью накапливать энер­гию в магнитном поле катушки . Из соотношения (2.1) видно, что ток через индуктивность  отстает от напряжения  на угол  (рис. 2.4).

Рис. 2.4. Гармонический ток и напряжение в катушке индуктивности

Переменный ток, протекая по виткам катушки, создает в проводни­ках тепловые потери мощности , где  – активное сопротивление обмотки. На рис. 2.5, б показана низкочастотная схема замеще­ния катушки индуктивности, состоящая из индуктивности  и активного сопротивления обмотки . Если сопротивлением обмот­ки можно пренебречь, то такую катушку считают идеальной индук­тивностью (рис. 2.5, в).

 

Конденсатор

Конденсатор является элементом электрической цепи, имеющим две проводящие обкладки, между которыми находится слой диэлек­трика (рис. 2.5, а). Если к зажимам конденсатора (рис. 2.5, а) подклю­чить источник синусоидального напряжения 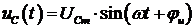, то на его обкладках возникнет изменяющийся во времени электриче­ский заряд , т. е. через конденсатор будет протекать электрический ток

 

,

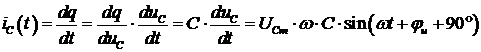(2.3)

Рис. 2.5. Схемы замещения конденсатора

 

где - емкость конденсатора, которая определяет зависи­мость изменения величины заряда на обкладках конденсатора от изме­нения напряжения, приложенного к его обкладкам, имеет размерность Фарада (Ф);  – реактивное емкостное сопротивление, имеет размерность Ом.

Из соотношения (2.3) видно, что ток через конденсатор  опере­жает напряжение  на угол  (рис. 2.6).

Рис. 2.6. Гармонический ток и напряжение в конденсаторе

 

Основной особенностью конденсатора является его способность запасать энергию электрического поля . Кроме того, в конденсаторе имеют место тепловые потери энергии в диэлектрике и обкладках, а также происходит запас энергии в магнитном поле. На рис. 2.5, б показана низкочастотная схема замещения конденсатора, состоящая из параллельного соединения емкости  и активного сопротивления с проводимостью - , учитывающей потери энергии в ди­электрике. Если этими потерями можно пренебречь, то конденсатор будет представлять собой идеальную емкость (рис. 2.5, в).

Из (2.3) следует, что при заданном токе  напряжение  можно найти по соотношению

.

(2.4)

 Если для установившегося синусоидального режима подставить ток 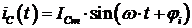 в (2.4), то напряжение на емкости примет вид:

.

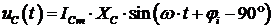(2.5)