1. RL-цепь
Рис. 2.12 – Исходная RL-цепь и схема ее замещения
Для цепи рис. 2.12, а заданы:
, 
, 
, 
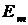и 
, 
;
.
Определить ток 
и напряжения 
и 
.
1. Определим параметры схемы замещения, рис. 2.12, б:
– реактивное индуктивное сопротивление;
– действующее значение ЭДС;
– комплекс действующего значения ЭДС;
2. Запишем второй закон Кирхгофа в комплексном виде:
 или  ,
| (2.18) |
где 
– комплексное сопротивление;
– модуль комплексного сопротивления:
| (2.19) |
– угол комплексного сопротивления
| (2.20) |
3. Найдем по закону Ома:
– комплекс действующего значения тока:
 ,
| (2.21) |
где 
– действующее значение тока;
– фаза тока
Определим комплекс действующего значения напряжения на резисторе
 ,
| (2.22) |
где 
– действующее значение напряжения на резисторе;
– комплекс действующего значения напряжения на индуктивности:
 ,
| (2.23) |
где 
– действующее значение напряжения на индуктивности
4. Запишем мгновенные значения тока и напряжений:
– ток в цепи;
– напряжение на резисторе;
– напряжение на индуктивности.
5. Построим векторные диаграммы токов и напряжений (рис. 2.13).
Рис. 2.13. Векторные диаграммы токов и напряжений 
-цепи.
6. Определим мощность в цепи.
• Мощность, отдаваемая источником:
– комплексная мощность
;
– активная мощность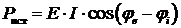 
(Вт);
– реактивная мощность 
(Вар);
– полная мощность 
(ВА).
• Мощность потребителя - катушки индуктивности:
– комплексная мощность 
– активная мощность 
(Вт);
– реактивная мощность 
(Вар),
где 
(рис. 2.13).
• Баланс мощности: 
;
R C -цепь
Рис. 2.15. Исходная 
-цепь и ее схема замещения
Для цепи рис. 2.15, и заданы:
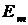, , , и 
, ;
.
Определить ток и напряжения 
и .
1. Определяем параметры схемы замещения (рис. 2.15, б)
– реактивное емкостное сопротивление 
;
– действующее значение ЭДС ;
– комплекс действующего значения ЭДС
2. Записываем второй закон Кирхгофа в комплексном виде:
,
или
,
где 
3. Найдем по закону Ома:
– комплекс действующего значения тока:
,
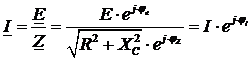где 
– действующее значение тока
– фаза тока.
– модуль комплексного сопротивления 
;
– угол комплексного сопротивления 
– комплекс действующего значения напряжения на резисторе:
,
где – действующее значение напряжения на резисторе;
– комплекс действующего значения напряжения на емкости:
,
где 
– действующее значение напряжения на емкости.
4. Запишем мгновенные значения тока и напряжений:
– ток в цепи;
– напряжение на резисторе;
– напряжение на емкости.
5. Построим векторные диаграммы токов и напряжений (рис. 2.16).
Рис. 2.16. Векторные диаграммы токов и напряжений -цепи
6. Определим мощность в цепи.
• Мощность, отдаваемая источником:
– комплексная мощность
;
– активная мощность 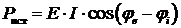(Вт);
– реактивная мощность (Вар);
– полная мощность (ВА).
• Мощность потребителя – емкости:
– комплексная мощность 
– активная мощность (Вт);
– реактивная мощность 
(Вар),
где (рис. 2.13).
• Баланс мощности: ;
