Для того, чтобы БФ была полной, необходимо и достаточно, чтобы она включала хотя бы одну функцию: несохраняющую константу 0, несохраняющую константу 1, несамодвойственную, нелинейную, немонотонную.
Теорему понимают так: одна и та же функция может представлять в функционально полной системе (ФПС) одно или несколько требуемых свойств, если она обладает этими свойствами. Таблица характеризует свойства БФ с позиций функциональной полноты (знаком ´ отмечены свойства, которыми обладает данная функция).
| Свойства | ||||||
| БФ | Формулы | Несо-храня-ющие 0 | Несо-храня-ющие 1 | Несамо-двойст-венность | Нели-ней-ность | Немо-нотон-ность |
| Константа 0 | 0 | ´ | ´ | |||
| Константа 1 | 1 | ´ | ´ | |||
| Отрицание | 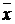
| ´ | ´ | ´ | ||
| Конъюнкция | x 1 x 2 | ´ | ´ | |||
| Дизъюнкция | x 1 Ú x 2 | ´ | ´ | |||
| Импликация | x 1 ® x 2 | ´ | ´ | ´ | ´ | |
| Эквивалентность | x 1 ~ x 2 | ´ | ´ | ´ | ||
| Отрицание импликации | x 1 x 2 | ´ | ´ | ´ | ´ | |
| Сумма по модулю 2 | x 1Å x 2 | ´ | ´ | ´ | ||
| Штрих Шеффера | x 1 | x 2 | ´ | ´ | ´ | ´ | ´ |
| Стрелка Пирса | x 1 ¯ x 2 | ´ | ´ | ´ | ´ | ´ |
Из таблицы видно, что операции: дизъюнкция и отрицание, конъюнкция и отрицание, штрих Шеффера, стрелка Пирса удовлетворяют теореме о функциональной полноте.
Система операций АЖ (сумма по модулю 2 и конъюнкция) вместе с константой 1 образуют ослабленно - функционально полную систему. Выбрав любую, неэлементарную функцию и дополнив ее одной или несколькими другими функциями так, чтобы они вместе удовлетворяли теореме о функциональной полноте, можно выразить через них все другие БФ.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется безынверсной(нормальной) формой логической функции?
2. Дайте определение дизъюнктивной нормальной формы логической функции.
3. Дайте определение конъюнктивной нормальной формы логической функции.
4. Укажите способы приведения логической функции к нормальной форме.
5. Что такое минитерм k-того ранга?
6. Что называется совершенной дизъюнктивной нормальной формой логической функции?
7. Что называется совершенной конъюнктивной нормальной формой логической функции?
8. Перечислите способы перехода от нормальных к совершенным нормальным формам БФ.
9. В чем смысл аналитического способа перехода к совершенной нормальной форме логической функции?
10. Что представляет собой графический способ перехода к совершенной нормальной форме логической функции?
11. Опишите принципы составления карт Карно.
12. Что представляет собой алгебра Жегалкина?
13. Перечислите пять типов логических функций.
14. Какая система функций называется функционально полной?
15. Дайте определение функциональной полноты.
16. Приведите теорему о функциональной полноте.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Приведите заданную булеву функцию к нормальной(безынверсной) форме:
а) Y 1 =  ;
;
б) Y 2 =  ;
;
в) Y 3 =  ;
;
г) Y 4 =  ;
;
д) Y 5 = 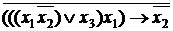 .
.
2. Преобразовать следующие логические функции в совершенную нормальную форму аналитическим способом:
а) Y = A Ú  C Ú
C Ú  B
B  ;
;
б) Y =  B Ú A
B Ú A  Ú
Ú  C;
C;
в) Y = A 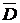 Ú B C Ú
Ú B C Ú 

 Ú B
Ú B  D;
D;
г) Y = (A Ú  Ú
Ú  ) (
) ( Ú C Ú D) (
Ú C Ú D) ( Ú B Ú
Ú B Ú 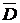 );
);
д) Y = (A Ú  ) (
) ( Ú C Ú
Ú C Ú 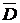 ) (B Ú D);
) (B Ú D);
е) Y =  (A Ú D) (
(A Ú D) ( Ú
Ú  Ú
Ú 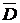 ).
).
3. Преобразовать логические функции, заданные в предыдущем пункте, к совершенной нормальной форме с использованием карт Карно.
За основу для построения нормальных форм булевых функций взяты операции конъюнкции и дизъюнкции. Соответственно различают дизъюнктивную и конъюнктивную нормальную формы булевых функций.
Система функций, суперпозицией которых представляется любая функция из некоторого множества булевых функций, называется функционально полной. Функционально полная систем функций образует базис в логическом пространстве.
Глава 14. Логические схемы
Бог сотворил мир на основе математических принципов.
И. Ньютон
Методы минимизации логических функций, основные элементы реализующие логические функции, карты Карно, метод Квайна, метод Блейка-Порецкого
ЦЕЛИ
Освоив эту главу, учащиеся должны знать и уметь:
· типы логических элементов, реализующих булевы функции;
· применять методы минимизации логических функций;
· строить логические схемы булевых функций.
14.1. Реализация булевых функций
Устройства, реализующие элементарные БФ, называются логическими элементами. Их входы соответствуют булевым переменным, а выходы – реализуемой функции.
На рис. 14.1 приведены логические элементы, реализующие элементарные БФ и примеры соответствия логических элементов и БФ.

Рис. 14.1. Соответствие логических элементов и булевых функций
По европейским и американским стандартам основные логические элементы обозначаются несколько иначе. Основные типы вентилей с точки зрения логических функций представлены в табл. 14.1.
Таблица 14.1
| Название вентиля | Символ логической схемы | Логическая функция |
| И | 
| 
|
| ИЛИ | 
| 
|
| НЕТ | 
| 
|
| И-НЕ | 
| 
|
| ИЛИ-НЕ | 
| 
|
| ИСКЛЮЧАЮЩЕЕ ИЛИ | 
| 
|
| СОЕДИНИТЕЛЬ | 
| 
|
В таблице наряду с названием логического элемента и логическим символом приведена его функция в виде логического выражения. Следует обратить внимание на то, что кружок означает логическое отрицание. Три типа логических схем — И, ИЛИ, НЕ, — представленные в табл. 14.1, соответствуют операциям булевой алгебры — конъюнкции, дизъюнкции и инверсии. С точки зрения возможности реализации произвольной логической функции эти три типа элементов образуют полный набор. Как следует из рис. 14.2, используя только элементы И и НЕ, можно получить элемент ИЛИ, поэтому сами по себе элементы И и НЕ составляют полный набор.

Рис. 14.2. Пример получения логического элемента ИЛИ
Подобно суперпозиции функций логические схемы образуются суперпозицией элементов посредством объединения их внешних узлов.
Задачи применения ЛС состоят в том, чтобы обеспечить экономичную реализацию БФ в некотором базисе.
Например, ЛС, реализующая функцию,
Y = (x 1 | x 2)Å( ® x 1).
® x 1).
Переведем в базис (НЕ, И, ИЛИ) (рис.14.3):
y = 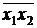 Å(x 3 Ú x 1) =
Å(x 3 Ú x 1) =  .
.
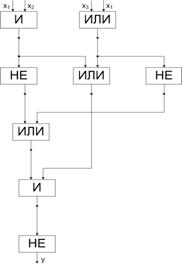
а)
Рис. 14.3. Схема логической функции
Та же ЛС, но упрощенная (рис.14.4).

б)
Рис. 14.4. Логическая схема функции после минимизации
Всегда можно построить много различных ЛС, соответствующих данной ЛФ, они все эквивалентны. Из множества эквивалентных ЛС можно выделить экономичную.
Каноническая задача синтеза (т.е. построения) ЛС в булевом базисе сводится к минимизации БФ, т.е. к представлению их ДНФ, содержащей наименьшее число букв. Такие формы называются минимальными.
Логические функции, заданные булевыми выражениями, которые содержат операции логического произведения, суммы и исключающей суммы, а также операцию логического отрицания, легко могут быть реализованы комбинациями логических элементов. Булевы выражения, как показано на рис. 14.5, могут быть подвергнуты разложению по «дереву вычислений» в соответствии со скобками и приоритетом операций.

Рис. 14.5. Пример синтеза логической схемы по булевой функции
Разложение по дереву вычислений начинается с последней вычисляемой операции булевого выражения. В примере, приведенном на рис. 14.5, последней в булевом выражении вычисляется операция исключающей суммы (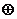 ), поэтому можно получить частичное разложение, показанное на рис. 14.5, б. Поскольку операция
), поэтому можно получить частичное разложение, показанное на рис. 14.5, б. Поскольку операция 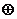 представляет собой двухместную операцию, на дереве вычислений имеются 2 операнда. Один из этих двух операндов –
представляет собой двухместную операцию, на дереве вычислений имеются 2 операнда. Один из этих двух операндов – 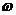 – представляет собой переменную и дальнейшему разложению не подлежит. Другой операнд –
– представляет собой переменную и дальнейшему разложению не подлежит. Другой операнд – 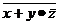 – представляет собой булево выражение и может быть разложен дальше. Последней вычисляемой операцией в выражении
– представляет собой булево выражение и может быть разложен дальше. Последней вычисляемой операцией в выражении 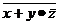 является операция логического отрицания, и разложение принимает вид, показанный на рис. 14.5, в. Дальнейшие аналогичные операции разложения приводят к виду, показанному на рис. 14.5, г. Когда операнд логического отрицания (–) представляет собой переменную и дополнение (отрицание) этой переменной может быть использовано в схеме, то в разложении нет необходимости.
является операция логического отрицания, и разложение принимает вид, показанный на рис. 14.5, в. Дальнейшие аналогичные операции разложения приводят к виду, показанному на рис. 14.5, г. Когда операнд логического отрицания (–) представляет собой переменную и дополнение (отрицание) этой переменной может быть использовано в схеме, то в разложении нет необходимости.
Для того чтобы по дереву разложения, соответствующему булеву выражению, сформировать цепь логических элементов, на дереве следует произвести замену операции логического произведения на элемент И, логической суммы — на элемент ИЛИ, исключающей логической суммы — на элемент ИСКЛЮЧАЮЩЕЕ ИЛИ и операции логического отрицания — на элемент НЕ. На рис. 14.6 показан результат такой подстановки, выполненной по дереву (рис. 14.5, г). Корень исходного дерева становится выходом, а его ветви — входами.

Рис. 14.6. Реализация логической схемы по булевой функции
14.2. Минимизация булевых функций
«При проектировании логической схемы возникает задача минимизации оборудования, используемого в схеме. Простейшей оценкой затрат оборудования на построение схемы, реализующей заданную функцию, является цена схемы по Квайну SQ, которая представляет собой суммарное количество входов во все логические элементы схемы. Задача минимизации цены схемы связана с задачей минимизации булевой функции, описывающей закон функционирования этой схемы. Обычно задача минимизации булевых функций решается с применением нормальных форм (ДНФ или КНФ). Нормальная форма булевой функции, содержащая минимальное количество букв, называется минимальной нормальной формой (МДНФ или МКНФ). Задача минимизации булевых функций сводится к нахождению их минимальных покрытий, т.е. покрытий, обладающих минимальной ценой» (Довгий П.С., Поляков В.И.).
Под минимизацией понимают процесс упрощения булевых функций, сведения их к минимально возможной форме. Минимальной называется такая форма БФ, которая не допускает уже никаких сокращений. Минимизация БФ производится с помощью различных методов, среди которых можно выделить три.
1. Аналитический (метод последовательного исключения переменных).
2. Метод карт Карно.
3. Метод Квайна –Макласки.
Рассмотрим аналитический метод минимизации булевых функций.
В этом случае для минимизации используют известные законы и тождества алгебры логики. Процесс минимизации заключается в последовательных операциях группировки и выноса за скобки общих переменных с последующим их исключением.
Формула, представленная в ДНФ, упрощается многократным применением операций:
· склеивания a b Ú a  = a
= a
· поглощения a Ú a b = a, a Ú 
 b = a Ú b, (a Ú b) (a Ú
b = a Ú b, (a Ú b) (a Ú  ) = 0, a (a Ú b) = a, a (
) = 0, a (a Ú b) = a, a ( Ú b) = a b.
Ú b) = a b.
В результате приходим к аналитическому выражению, когда дальнейшие преобразования невозможны, т.е. получаем тупиковую форму.
Среди тупиковых форм находится и минимальная ДФ. Причем она может быть не единственной. Для проверки, что тупиковая форма минимальна, надо найти все тупиковые формы и сравнить их по числу входящих в них букв.
Например, функция задана СДНФ:
Y =  x 2
x 2  Ú
Ú  x 2 x 3 Ú x 1
x 2 x 3 Ú x 1 
 Ú x 1
Ú x 1  x 3 Ú x 1 x 2 x 3.
x 3 Ú x 1 x 2 x 3.
Группируя члены и применяя операцию склеивания, получим
Y = ( x 2
x 2  Ú
Ú  x 2 x 3) Ú (x 1
x 2 x 3) Ú (x 1 
 Ú x 1
Ú x 1  x 3) Ú x 1 x 2 x 3 =
x 3) Ú x 1 x 2 x 3 =  x 2 Ú x 1
x 2 Ú x 1  Ú x 1 x 2 x 3.
Ú x 1 x 2 x 3.
Но эта форма не минимальна (7 букв).
При повторении в исходной формуле одного члена (это возможно, т.к. x Ú x = x) получим:
Y =  x 2 Ú x 1
x 2 Ú x 1  Ú (x 1 x 2 x 3 Ú
Ú (x 1 x 2 x 3 Ú  x 2 x 3) =
x 2 x 3) =  x 2 Ú x 1
x 2 Ú x 1  Ú x 2 x 3 (6 букв).
Ú x 2 x 3 (6 букв).
Каждой вершине n -мерного куба можно поставить в соответствие конституенту единицы. Подмножество отмеченных вершин является отображением на n -мерном кубе БФ от n переменных в СДНФ. На рис. 14.7 показан пример отображения БФ 3-х переменных на трехмерном кубе.

Рис. 14.7. Пример отображения БФ 3-х переменных на трехмерном кубе
Для отображения функции от n переменных, представленной в любой ДНФ, необходимо установить соответствие между ее минитермами (конституентами единицы) и элементами n -мерного куба.
Минитерм (n - 1)-го ранга j n - 1 — это результат склеивания двух минитермов n -го ранга, т.е. j n - 1 = j n - 1 xi Ú j n - 1 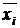 . На n -мерном кубе это соответствует замене двух вершин, отличающихся только значениями координаты xi, соединяющим эти вершины ребром.
. На n -мерном кубе это соответствует замене двух вершин, отличающихся только значениями координаты xi, соединяющим эти вершины ребром.
Говорят, что ребро покрывает инцидентные ему вершины. Таким образом, минитермам (n - 1)-го порядка соответствуют ребра n -мерного куба. Аналогично устанавливается соответствие минитермов (n - 2)-го порядка граням n -мерного порядка, каждая из которых покрывает 4 вершины и четыре ребра.
Например: Y =  x 2 Ú x 1
x 2 Ú x 1  Ú x 3. На рис. 14.8 показана графическая реализация данной функции.
Ú x 3. На рис. 14.8 показана графическая реализация данной функции.

Рис. 14.8. Графическая реализация функции y
Покрытие, соответствующее минимальной форме, называется минимальным покрытием.
Например, неминимальная форма y =  x 2 Ú x 1
x 2 Ú x 1  Ú x 1 x 3 Ú x 2 x 3 соответствует покрытию куба (рис. 14.9):
Ú x 1 x 3 Ú x 2 x 3 соответствует покрытию куба (рис. 14.9):

Рис. 14.9. Вариант покрытия куба
А покрытию Y =  x 2 Ú x 1
x 2 Ú x 1  Ú x 1 x 3 соответствует минимальная форма (рис. 14.10):
Ú x 1 x 3 соответствует минимальная форма (рис. 14.10):

Рис. 14.10. Покрытие куба минимальной формой
Отображение функции на n-мерном кубе наглядно при n £ 3. При n > 4 требуется много сложных построений.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
14.1. Используя законы алгебры логики, минимизировать логическую функцию:
а) Y = x 1 x 2 Ú 
 Ú x 1 x 2 х 3 Ú х 1
Ú x 1 x 2 х 3 Ú х 1 
 .
.
Решение. Применив метод группировки, описанный выше, получим:
x 1 x 2 Ú x 1 x 2 х 3 = x 1 x 2 (1 Ú х 3) = x 1 x 2;

 Ú х 1
Ú х 1 
 =
= 
 (1 Ú х 1) =
(1 Ú х 1) = 
 .
.
Ответ. Y = x 1 x 2 Ú 
 .
.
б) Y = x 1 х 3 Ú x 1 x 2 х 3 Ú  х 3 Ú
х 3 Ú 

 Ú x 2 х 3.
Ú x 2 х 3.
Решение. После группировки получим:
 х 3 Ú
х 3 Ú 

 =
=  (х 3 Ú
(х 3 Ú 
 );
);
x 1 х 3 Ú x 1 x 2 х 3 = x 1 х 3 (1 Ú х 2) = х 1 х 3.
Применим распределительный закон для логического умножения:
 (х 3 Ú
(х 3 Ú 
 ) =
) =  (
( Ú х 3) (х 3 Ú
Ú х 3) (х 3 Ú  ) =
) =  (
( Ú х 3) =
Ú х 3) =  x 2 Ú
x 2 Ú  х 3.
х 3.
После этого получим следующее выражение:
Y = 
 Ú
Ú  х 3 Ú x 2 х 3 Ú x 1 х 3.
х 3 Ú x 2 х 3 Ú x 1 х 3.
Продолжая процесс группировки, получим:
х 3 (x 1 Ú  ) Ú
) Ú 
 Ú x 2 х 3 = х 3 Ú
Ú x 2 х 3 = х 3 Ú 
 Ú x 2 х 3 = х 3 (1 Ú x 2) Ú
Ú x 2 х 3 = х 3 (1 Ú x 2) Ú 
 = х 3 Ú
= х 3 Ú 
 .
.
Ответ. Y = х 3 Ú 
 .
.
в) Y = А 
 Ú А В
Ú А В  Ú A B C.
Ú A B C.
Решение. Воспользуемся для минимизации исходной функции знакомым нам методом группировки:
Y = А 
 Ú A B
Ú A B  Ú A B C = A
Ú A B C = A 
 Ú A B (
Ú A B ( Ú C) = A
Ú C) = A 
 Ú A B = A (
Ú A B = A (
 Ú B) = A (
Ú B) = A ( Ú B) (
Ú B) ( Ú B) = A (
Ú B) = A ( Ú B)
Ú B)
Ответ. Y = A ( Ú B).
Ú B).
14.3. Карты Карно
«Карты Карно являются одним из способов таблично-графического представления булевых функций. Они используются для минимизации булевых функций от небольшого числа переменных (как правило, от трех до шести). С использованием карт Карно достаточно просто выделяется минимальное покрытие функции, по которому составляется МДНФ (для единичного покрытия) или МКНФ (для нулевого). Для этой цели на карте выделяются максимальные кубы, представляемые прямоугольниками из клеток, отмеченных единицами или нулями. Две соседние клетки карты образуют 1-куб, четыре - 2-куб, восемь - 3-куб и т.д. Покрытие с минимальной ценой формируется, если каждая существенная вершина будет покрыта максимальным кубом наибольшей размерности и для покрытия всех существенных вершин будет использовано наименьшее число кубов» (Довгий П.С., Поляков В.И.).
Минимизация с помощью карт Карно производится следующим образом.
1. Строится карта Карно.
2. В соответствии с алгоритмом, описанным выше, карта Карно заполняется единицами.
3. Производится минимизация. В основу процесса минимизации положен следующий принцип: две стоящие рядом единицы могут быть объединены.
При этом переменная, значение которой изменяется, исключается из дальнейшего рассмотрения.
Соответственно, при объединении четырех расположенных рядом единиц одновременно исключаются из рассмотрения две переменных, восьми единиц - три и т.д.
4. Полученная в результате процесса минимизации функция будет являться минимальной.
Карты Карно представляют собой специальные таблицы соответствия. Столбцы и строки таблиц соответствуют всевозможным наборам значений не более двух переменных. Причем эти наборы расположены в таком порядке, что каждый последующий отличается от предыдущего значением только одной из переменных, поэтому и соседние клетки таблицы по горизонтали и вертикали отличаются значением только одной переменной. Клетки, расположенные по краям таблицы, также считаются соседними и обладают этим свойством. Клетки наборов, на которых функция принимает значение 1, заполняются единицами (рис. 14.11, 14.12, 14.13).
| 00 | 01 | 11 | 10 |
| (x 1, x 2) | |||
Рис. 14.11. Карта Карно для двух переменных
| 00 | 01 | 11 | 10 | ||
| (x 1) | 0 | ||||
| 1 | |||||
| (x 2, x 3) | |||||
Рис. 14.12. Карта Карно для трех переменных
| 00 | 01 | 11 | 10 | ||
| (x 1, x 2) | 00 | ||||
| 01 | |||||
| 11 | |||||
| 10 | |||||
| (x 3, x 4) | |||||
Рис. 14.13. Карта Карно для четырех переменных
Например, для функции Y = x 1  Ú x 2 x 4 Ú
Ú x 2 x 4 Ú  x 3
x 3  (НДФ) (рис.14.14).
(НДФ) (рис.14.14).
| x 3 | |||||
| 1 | x 2 | ||||
| x 1 | 1 | 1 | 1 | ||
| 1 | 1 | 1 | |||
| 1 | 1 | ||||
| x 4 | |||||
Рис. 14.14. Заполнение карты Карно для функции Y
Для упрощения строки и столбцы, соответствующие значениям 1 для некоторой переменной, выделяются фигурной скобкой с обозначением этой переменной.
Покрытие соответствует минимальной дизъюнктивной форме.
Считывание минитермов осуществляется по правилу: клетки, образующие S -куб, дают минитерм (n - s)-го ранга, в который входят те (n - s) переменные, которые сохраняют одинаковые значения на этом S кубе, причем значениям 1 соответствуют сами переменные, а значениям 0 — их отрицания. Переменные, которые не сохраняют свои значения на S -кубе, в минитермах отсутствуют.
Различные способы считывания приводят к различным представлениям функции в ДНФ. Например, по одной и той же карте Карно (рис. 14.15) после считывания можно записать несколько вариантов представления одной функции.
| x 2 | ||||
| 1 | 1 | |||
| x 1 | 1 | 1 | 1 | |
| х 3 | ||||
Рис. 14.15. Карта Карно для трех аргументов
Y1 = x 1  Ú x 1 x 3 Ú x 2 х 3 Ú
Ú x 1 x 3 Ú x 2 х 3 Ú  x 2;
x 2;
Y2 = x 1  Ú x 1 x 2 х 3 Ú
Ú x 1 x 2 х 3 Ú  x 2;
x 2;
Y3 = x 1  Ú x 2 х 3 Ú
Ú x 2 х 3 Ú  x 2.
x 2.
Построим карту Карно для пяти аргументов A, B, C, D, E, F (рис. 14.16).
| E |
| E | |||||||
| A | 
| ||||||||
| C | |||||||||
|
| |||||||||

| |||||||||
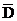
| D |
| D | 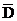
| |||||
| B |
| ||||||||
Рис. 14.16. Карта Карно для пяти аргументов
При большом числе переменных БФ представляется комплексом кубов (КК).
КК K (y) функции y = f (x 1, x 2,..., xn) определяется как объединение множеств KS (y) всех ее S -кубов (S = 0, 1,..., n), т.е. K (y) = È KS (y), причем некоторые из KS (y) могут быть пустыми.
Для записи S -кубов и минитермов функции от n переменных используются слова длины n, буквы которых соответствуют всем n переменным.
Входящие в минитерм переменные называются связанными и представляются значениями, при которых минитерм равен 1 (1 для xi, и 0 для 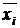 ). Не входящие в минитерм переменные являются свободными и обозначаются x.
). Не входящие в минитерм переменные являются свободными и обозначаются x.
Например, 2-куб функции пяти переменных соответствующий минитерму x 2  x 5, запишется:
x 5, запишется:
x 1 0 x 1
(x 1 x 2 x 3 x 4 x 5).
0-кубы, соответствующие конституентам 1, представляются наборами значений переменных, на которых функция равна 1. Для удобства слова S-кубов располагают в столбцы, а их совокупность – в фигурные скобки.
Например, КК, соответствующий представлению функции на трехмерном кубе, выражается следующим образом:
K (y) = K 0 È K 1 È K 2.
 .
.
Графическая интерпретация данного выражения представлена на рис. 14.17,а,б.


Рис. 14.17,а,б. Графическая интерпретация
Комплекс кубов образует максимальное покрытие функции. Исключая из него все те S -кубы, которые покрываются кубами высшей размерности, получаем покрытия, соответствующие тупиковым формам. Так, для примера имеем:
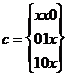 ,
,
которое соответствует функции y =  x 3 Ú x 2
x 3 Ú x 2  Ú
Ú  . В данном случае это покрытие является минимальным.
. В данном случае это покрытие является минимальным.
Приведем постановку задачи минимизации БФ. Минимизация БФ сводится к поиску минимальной ДФ, которой соответствует минимальное покрытие. Общее число букв, входящих в нормальную форму, выражается ценой покрытия:
С =  ,
,
где qs — число S -кубов, образующих покрытие данной функции от n переменных.
Задача минимизации решается в 2 шага:
1 шаг. Сначала ищут сокращенное покрытие, которое включает все S-кубы максимальной размерности, но не содержит ни одного куба, покрывающего каким-либо кубом того покрытия. Соответствующую ДНФ называют сокращенной, а ее минитермы — простыми импликантами.
2 шаг. Переход от сокращенной ДНФ к тупиковым ДНФ. Из них выбираются минимальные.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 14.2. Минимизировать с помощью карт Карно БФ:
а) Y = А  С Ú
С Ú 
 C Ú
C Ú 

 Ú
Ú  B
B  Ú A B C Ú A B
Ú A B C Ú A B  .
.
Решение. Строим карту Карно (рис. 14.18).
| С\AB |  00 00
|  01 01
| 11 | 10 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 |  1 1
| 1 |
Рис. 14.18. Пример минимизации функции трех переменных (СДНФ)
В полученной карте Карно группируем соседние единицы по горизонтали и вертикали. Так, например, объединив единицы, как показано в вышеуказанной таблице, мы получим следующую минимальную БФ:
Y 1 мин. = 
 Ú B
Ú B  Ú A C.
Ú A C.
Выполнив группировку иначе, так, например, как показано на рис. 14.19, получим иной вариант минимальной БФ:
Y 2 мин =  С Ú
С Ú 
 Ú A B.
Ú A B.
| С\АВ |  00 00
| 01 |  11 11
| 10 |
| 0 | 1 | 1 | 1 | 0 |
| 1 |  1 1
| 0 | 1 |  1 1
|
Рис. 14.19. Второй вариант группировки переменных
Очевидно, что эти два варианта равнозначны, поскольку содержат одинаковое число СНФ.
Ответ. Y 1 мин. = 
 Ú B
Ú B  Ú A C либо Y 2 мин =
Ú A C либо Y 2 мин =  С Ú
С Ú 
 Ú A B.
Ú A B.
б) Х = А  С D Ú A
С D Ú A 
 D Ú A B
D Ú A B  D Ú
D Ú  B C
B C 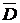 Ú
Ú  B C D Ú
B C D Ú  B
B  D Ú
D Ú 
 C D Ú
C D Ú 

 D Ú
D Ú 


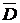 Ú A
Ú A 

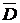 .
.
Решение. Уже известным нам способом строим карту Карно (рис. 14.20).
Затем группируем соседние единицы. В результате группировки получаем следующий результат:
YДНФ мин. = A Ú 
 Ú
Ú  B C.
B C.
| CD\AB | 00 | 01 | 11 | 10 |
| 00 |   1 1
| 0 | 0 |  1 1
|
| 01 | 1 | 1 | 1 | 1 |
| 11 | 1 |  1 1
| 1 | 1 |
| 10 | 0 | 1 | 0 | 0 |
Рис. 14.20. Пример минимизации функции 4-х переменных (СДНФ)
Для того, чтобы записать по полученной карте Карно ХКНФ мин необходимо провести группировку по нулям (рис. 14.21):
| CD\AB | 00 | 01 | 11 | 10 |
| 00 | 1 |  0 0
| 0 | 1 |
| 01 | 1 | 1 | 1 | 1 |
| 11 | 1 | 1 | 1 | 1 |
| 10 |  0 0
| 1 |  0 0
|  0 0
|
Рис. 14.21. Пример минимизации функции 4-х переменных (СКНФ)
После группировки соседних единиц получим выражение:
В 
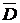 Ú
Ú  C
C 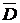 Ú A C
Ú A C 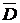
Теперь для того, чтобы получить ХКНФ мин, достаточно проинвертировать полученное выражение:
Y КНФ мин = 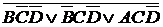 = (
= ( Ú C Ú D) (B Ú
Ú C Ú D) (B Ú  Ú D) (A Ú
Ú D) (A Ú  Ú D).
Ú D).
14.4. Метод Квайна - Мак-Класски
Этот метод применяется для минимизации БФ, содержащих небольшое количество переменных (как правило не более 4-х), причем исходная функция должна быть записана в виде СДНФ.
Минимизация выполняется в два этапа:
Й этап
Сначала производится выделение из СДНФ так называемых сокращенных нормальных форм. Для этого строится таблица, по строкам и столбцам которой записываются все составляющие БФ конъюнкции.
Затем производится анализ полученных конъюнкций и для тех конъюнкций, которые отличаются друг от друга на одну переменную, производится операция склеивания, а на пересечении соответствующей строки и столбца записывается результат операции склеивания, т.е. сокращенная нормальная форма (СНФ).
Й этап
Составляется новая таблица, в которой строкам соответствуют полученные на предыдущем этапе сокращенные нормальные формы, а столбцам - конъюнкции, составляющие исходную функцию.
Затем проверяется условие вхождения сокращенных форм в каждую из имеющихся исходных конъюнкций.
Там, где данное условие выполняется, на пересечении соответствующей строки и столбца ставится знак «плюс».
После этого записывается минимальная функция, которая определяется как минимальный набор сокращенных форм, полностью покрывающий исходный набор конъюнкций.
Метод используется, когда функция задана в СДНФ или таблицей соответствия. Приведение к сокращенной форме осуществляется последовательным применением операции склеивания: axi Ú a 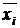 = a.
= a.
Множеству конституент единицы, представленных в исходной форме, соответствует совокупность 0-кубов K 0, а операция склеивания – объединению двух 0-кубов, которые отличаются только одной координатой. Результатом такого объединения является 1-куб, в котором различные координаты исходных 0-кубов замещены символом х. Сравнивая попарно все 0-кубы, получаем множество 1-кубов K 1. Применяя к K 1 операцию склеивания, находим множество 2-кубов K 2 и т.д. Это продолжается до тех пор, пока получаемое из KS очередное KS +1 не окажется пустым множеством. В результате множество K 0 преобразуется в комплекс кубов:
K = { K 0, K 1,..., KS }, причем S £ n.
Для выделения из K множества простых импликант Z Ì K при каждой операции склеивания необходимо отмечать меткой (например D) те кубы, которые объединяются в кубы высшей размерности.
Очевидно, неотмеченные кубы и образуют множество простых импликант Z. Чтобы уменьшить число сравниваемых пар при операции объединения, целесообразно разбить множество KS на классы, в каждом из которых содержатся S -кубы с одинаковым числом единиц, и упорядочить эти классы по возрастающему числу единиц. Так как объединяться могут только такие 2 S -куба, число единиц, в которых
точно на одну больше или меньше, то достаточно ограничиться попарным сравнением S -кубов одного класса с S -кубами соседнего класса.
На втором шаге для образования минимального покрытия используется таблица покрытий. Ее строки соответствуют импликантам, а столбцы конституентам единицы СДНФ данной функции, которые представляются 0-кубами (вершинами) комплекса кубов. В клетку таблицы записывается метка, если простая импликанта в данной строке покрывает вершину в данном столбце. Экстремалям соответствуют те строки таблицы, которые содержат единственную метку в каком-либо столбце. Удаляя строки экстремалей и все столбцы, в которых эти строки имеют метки, получаем более простую таблицу. На ее основе выбираем простые импликанты, которые дополняют выделенное множество экстремалей до минимального покрытия функции.
Пример 14.3. Задана функция 4 переменных y = f (x 1, x 2, x 3, x 4) таблицей соответствия:
| x 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| x 2 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| x 3 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| x 4 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| y | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
Ей соответствует СДНФ:
y = 









