Стрелка Пирса - приводится к виду 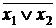 и называется операцией ИЛИ - НЕ.
и называется операцией ИЛИ - НЕ.
Штрих Шеффера - можно привести к виду 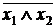 и называется операцией И - НЕ.
и называется операцией И - НЕ.
Функцииотрицания импликации (прямой и обратной) называются иначе функциями запрета по х 1 и х 2 соответственно и читаются (не х 2, а х 1) и наоборот.
Всякая функция от меньшего числа переменных содержится среди функций большего числа переменных. Между функциями имеются зависимости, на основании которых можно записать соотношения для констант 0 =  и 1 =
и 1 =  , для функции одной переменной х =
, для функции одной переменной х =  и для функций двух переменных: x 1 x 2 =
и для функций двух переменных: x 1 x 2 =  ,
,  =
=  , x 1 Ú x 2 =
, x 1 Ú x 2 =  .
.
Любая функция двух переменных (включая константы) выражается в аналитической форме через совокупность шести функций, содержащей отрицание 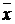 и любую из каждой пары функций:
и любую из каждой пары функций:
{ y 0, y 15}, { y 1, y 14}, { y 2, y 13}, { y 6, y 9}, { y 7, y 8}.
Например, такой совокупностью могут быть функции: константа 0, отрицание 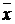 , конъюнкция х 1 Ù х 2, дизъюнкция x 1 Ú x 2, эквивалентность x 1 ~ x 2, импликация x 1 ® x 2.
, конъюнкция х 1 Ù х 2, дизъюнкция x 1 Ú x 2, эквивалентность x 1 ~ x 2, импликация x 1 ® x 2.
Выбранная совокупность шести функций является избыточной. Покажем, что эквивалентность и импликация выражаются через остальные функции этой совокупности:
x 1 ® x 2 =  Ú x 2, x 1 ~ x 2 = (
Ú x 2, x 1 ~ x 2 = ( Ú x 2)(x 1 Ú
Ú x 2)(x 1 Ú  ).
).
Для этого построим таблицу 12.6 и сравним ее с основной таблицей.
Таблица 12.6
| x 1 | 0 | 0 | 1 | 1 | |
| x 2 | 0 | 1 | 0 | 1 | |

| 1 | 1 | 0 | 0 | |

| 1 | 0 | 1 | 0 | |
 Ú x 2 Ú x 2
| 1 | 1 | 0 | 1 | x 1 ® x 2 |
x 1 Ú 
| 1 | 0 | 1 | 1 | |
( Ú x 2)(x 1 Ú Ú x 2)(x 1 Ú  ) )
| 1 | 0 | 0 | 1 | x 1 ~ x 2 |
Итак, комплект элементарных функций сокращается до четырех:
· константа 0,
· конъюнкция х 1 Ù х 2,
· отрицание 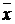 ,
,
· дизъюнкция x 1 Ú x 2.
Его можно сократить за счет законов де Моргана: x 1 Ú x 2 =  , x 1 Ù x 2 =
, x 1 Ù x 2 =  .
.
Булевы функции могут быть выражены через отрицание и конъюнкцию или через отрицание и дизъюнкцию. Более того, для записи любой БФ достаточно одной из 2 элементарных функций: стрелки Пирса или штриха Шефера.
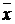 = х ¯ х = х | х, x 1 Ù x 2 = (x 1 ½ x 2) | (x 1 ½ x 2), x 1 Ú x 2 = (x 1 ¯ x 2)¯(x 1 ¯ x 2).
= х ¯ х = х | х, x 1 Ù x 2 = (x 1 ½ x 2) | (x 1 ½ x 2), x 1 Ú x 2 = (x 1 ¯ x 2)¯(x 1 ¯ x 2).
С помощью суперпозиции функций, т.е. подстановок в логические формулы вместо переменных, некоторых БФ получают более сложные функции от любого числа переменных.
Например, подставляя в формулу a * b выражение: a = x 1 Ú x 2, b = x 2 ® c, c =  получим (x 1 Ú x 2) (x 2 ®
получим (x 1 Ú x 2) (x 2 ®  ).
).
Таблица 12.7 для сложения формул записывается на основании общей таблицы для элементарных функций.
Например:
Таблица 12.7
| x 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| x 2 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| x 3 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| x 1 Ú x 2 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |

| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
x 2 ® 
| 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
(x 1 Ú x 2)(x 2 ®  ) )
| 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
Область определения БФ от n переменных y = f (x 1,..., xn) рассматривают как совокупность n -мерных векторов, компонентами которого являются буквы 0 и 1.
При n = 3 каждый вектор представляется вершиной единичного куба в трехмерном пространстве.
В общем случае совокупность векторов (x 1,..., xn) отображается на множество вершин n -мерного куба.
БФ отображается на n -мерном кубе путем выделения вершин, соответствующих векторам (x 1,..., xn), на которых БФ принимает значение 1.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Поясните термин “логическое высказывание”.
2. Какие логические операции вы знаете?
3. Назовите порядок выполнения логических операций в составном логическом высказывании.
4. Что называется логической формулой?
5. Каким образом задается логическая формула?
6. Как устанавливается равенство двух логических формул?
7. Как доказывается истинность логических формул, тождеств, законов?
8. Что такое булева функция?
9. Запишите все булевы функции «двух переменных».
10. Определите булевы функции «штрих Шеффера» и «стрелка Пирса».
11. Что такое функция отрицания импликации?
12. Приведите основные логические тождества и законы.
13. В чем заключается закон Де Моргана?
14. Каким образом доказывается справедливость основных логических законов и тождеств?
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Определить значения следующих составных высказываний:
а) ((x Ú  Ú
Ú  )
)  y) ® (x Ú
y) ® (x Ú  ) z, если х = 0; y = 1; z = 1.
) z, если х = 0; y = 1; z = 1.
б)  y ® (
y ® ( z Ú x y
z Ú x y  ® (x Ú z)), если х = 0; y = 1; z = 0.
® (x Ú z)), если х = 0; y = 1; z = 0.
в) x z ® (x Ú 
 z Ú y z) ® y
z Ú y z) ® y  , если х = 0; y = 0; z = 1.
, если х = 0; y = 0; z = 1.
г) ( y ® z) Ú (
y ® z) Ú ( ® x
® x  z) x z, если х = 1; y = 0; z = 1.
z) x z, если х = 1; y = 0; z = 1.
д) y ( Ú
Ú  y ® x z) Ú (x
y ® x z) Ú (x  ® (
® ( Ú z), если х = 1; y = 1; z = 1.
Ú z), если х = 1; y = 1; z = 1.
е) ((x Ú  z) ® (
z) ® ( z Ú y z)) (x
z Ú y z)) (x  Ú y
Ú y  ), если х = 1; y = 1; z = 1.
), если х = 1; y = 1; z = 1.
ж) ((x  ) ® (x
) ® (x  Ú
Ú  z)) Ú ((
z)) Ú ((
 Ú
Ú  z) ® (x y
z) ® (x y  Ú
Ú  y)), если х = 1; y = 1; z = 0.
y)), если х = 1; y = 1; z = 0.
2. Для составных логических высказываний, заданных в пункте 1, определить набор значений логических переменных x, y, z, при котором значение составного высказывания было бы: а) ложно; б)истинно.
Ответ записать в виде таблицы истинности.
3. Используя таблицы истинности, доказать справедливость следующих тождеств:
а) x Ú (y z) = (x Ú y) (x Ú z);
б) x (y Ú z) = (x y) Ú (x z);
в) x (x Ú z) = x;
г) x Ú (x y) = x;
д) (x y) Ú (x  ) = x;
) = x;
е) (x Ú y) (x Ú  ) = x;
) = x;
ж) x ® y =  Ú y;
Ú y;
з) x ® y =  ®
®  ;
;
и) (x ® y) (y ® x) = (x «y);
к)  ® y =
® y =  ® x = x Ú y;
® x = x Ú y;
л) x Ú y =  ;
;
м) x y =  ;
;
н)  =
= 
 ;
;
о)  =
=  Ú
Ú  .
.
3. Используя законы и тождества алгебры логики, доказать или опровергнуть справедливость следующих тождеств:
а)  ® y = y;
® y = y;
б)  ®
®  = x ® y;
= x ® y;
в)  = x y;
= x y;
г)  = 0;
= 0;
д)  =
= 

 .
.
Логика - это искусство рассуждений, наука о законах и формах мышления. Основная цель применения в логике символики - это свести операции с логическими заключениями к формальным действиям над символами. При этом исходные положения записываются формулами, которые преобразуются по определенным законам, а полученные результаты истолковываются в определенных понятиях.
Глава 13. Нормальные формы булевых функций
Логика – это искусство приходить к непредсказуемому выводу.
С. Джонсон
Нормальные формы булевых функций, дизъюнктивная и конъюнктивная нормальные формы, совершенная нормальная форма, способы перехода от нормальных к совершенным нормальным формам, алгебра Жегалкина, функциональная полнота булевых функций
ЦЕЛИ
Освоив эту главу, учащиеся должны знать и уметь:
· основные способы перехода от нормальных к совершенным нормальным формам;
· основные операции алгебры Жегалкина;
· строить нормальные формы булевых функций;
· определять функционально полные системы булевых функций.
13.1. Дизъюнктивная и конъюнктивная нормальные формы
В Булевой алгебре, как и в любой алгебре, существует принцип двойственности. Так, например, взаимно двойственными являются операции дизъюнкции и конъюнкции.
Дизъюнктивная (конъюнктивная) нормальная форма (ДНФ (КНФ)) — это дизъюнкция (конъюнкция) конечного числа различных членов, каждый из которых представляет собой конъюнкцию (дизъюнкцию) отдельных переменных или их отрицаний, входящих в данный член не более одного раза.
За основу для построения нормальных(безинверсных) форм БФ взяты операции конъюнкции и дизъюнкции. Соответственно различают дизъюнктивную нормальную форму (ДНФ) и конъюнктивную нормальную форму (КНФ) БФ.
Дизъюнктивной нормальной формой БФ называется функция, представляющая собой дизъюнкцию конечного числа конъюнкций, каждая из которых содержит простые переменные в прямой или инверсной форме; но не более одного раза для каждой конъюнкции.
Конъюнктивную нормальную форму БФ, по аналогии, можем определить как конъюнкцию некоторого числа дизъюнкций, содержащих не повторяющиеся в рамках каждой конъюнкции переменные в прямой или инверсной форме.
Любая формула приводится к нормальной форме следующим образом:
1) С помощью законов де Моргана формула преобразуется к такому виду, чтобы знаки отрицания относились только к отдельным переменным.
2) На основе первого (второго) дистрибутивного закона формула сводится к дизъюнкции конъюнкций (конъюнкции дизъюнкций).
3) Полученное выражение упрощается в соответствии с тождествами (1.7).
Любое высказывание может быть приведено к нормальной (безынверсной) форме. Для этого можно воспользоваться следующими методами:
1. Законами Де Моргана пользуются для избавления от знаков инверсии, распространяющихся на несколько переменных сразу.
2. Законы алгебры логики (дистрибутивность и т.д.) используют для приведения высказывания к ДНФ или КНФ.
3. Тождества алгебры логики используют для упрощения полученных выражений.
Элементарной конъюнкцией (дизъюнкцией) или конъюнктивным (дизъюнктивным) термом называется выражение, представляющее собой конъюнкцию (дизъюнкцию) любого конечного множества попарно различимых букв или состоящее из одной буквы.
Члены ДНФ (КНФ), представляющие собой элементарные конъюнкции (дизъюнкции) k букв, называются минитермами (макстермами) k -го ранга. Так, например, x y - в форме выше минитерм 2 ранга, (x Ú  ) - макстерм второго ранга.
) - макстерм второго ранга.
Введем также понятие совершенной нормальной формы БФ. Если в каждом члене нормальной формы представлены все переменные (либо в прямом, либо в инверсном виде), то она называется совершенной нормальной формой (СНФ).
Совершенной конъюнктивной нормальной формой БФ(СКНФ) называется логическая функция, представленная в конъюнктивной нормальной форме, причем каждая ее элементарная дизъюнкция содержит все возможные переменные в прямой или инверсной форме.
Соответственно, совершенной дизъюнктивной нормальной формой БФ (СДНФ) называется логическая функция, представленная в дизъюнктивной нормальной форме, при условии, что каждая составляющая ее элементарная конъюнкция содержит все возможные переменные в прямой или инверсной форме.
Любая БФ, не являющаяся тождественным нулем (единицей), имеет одну и только одну совершенную дизъюнктивную (конъюнктивную) нормальную форму (СДНФ (СКНФ)). Если какой-либо член в ДНФ не содержит переменной xi, то она вводится тождественным преобразованием:
j = j(xi Ú 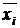 ) = j xi Ú j
) = j xi Ú j 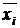 .
.
Совершенные нормальные формы можно записать для любой БФ, исходя из таблицы истинности этой функции, например, так, как показано в таблице БФ двух переменных.
В этом случае СДНФ записывается для тех значений наборов переменных, при которых БФ истина, т.е. принимает значение, равное единице. При этом, если значение переменной в строке равно 1, то переменная входит в конъюнкцию в прямом виде, а если 0 – то в обратном.
В свою очередь, СКНФ записывается для тех наборов переменных, при которых БФ обращается в 0.
Составляющие СКНФ элементарные дизъюнкции записываются следующим образом: если значение переменной в строке таблицы равно 0, то она записывается в прямом виде, если 1 - то в инверсном.
Для совокупности переменных х 1,..., х n выражение  x 2... xn называют конституентой единицы, а выражение
x 2... xn называют конституентой единицы, а выражение  Ú
Ú  Ú … Ú
Ú … Ú  – конституентой нуля (
– конституентой нуля ( означает либо xi, либо
означает либо xi, либо 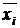 ).
).
Данная конституента единицы (нуля) образуется при одном соответствующем ей наборе значений переменных, который получается, если все переменные принять равными единице (нулю), а их отрицания – нулю (единице). Например, конституенте единицы x 1  x 3 x 4 соответствует набор (1011), а конституенте нуля
x 3 x 4 соответствует набор (1011), а конституенте нуля  Ú x 2 Ú
Ú x 2 Ú  Ú
Ú  – (1011).
– (1011).
В некоторых учебниках на основе конституент единицы (нуля) составляются канонические дизъюнктивные (конъюнктивные) нормальные формы булевых функций. ДНФ (КНФ) называется канонической или совершенной, если все ее элементарные конъюнкции (дизъюнкции) являются конституентами единицы (нуля) (Довгий П.С., Поляков В.И.).
Так как СДНФ (СКНФ) является дизъюнкцией (конъюнкцией) конституент единицы (нуля), то можно утверждать, что представляемая ею БФ f (x 1, x 2,..., xn) обращается в единицу (нуль) только при наборах значений переменных x 1, x 2,..., xn соответствующих этим конституентам. На остальных наборах эта функция обращается в нуль (единицу), как показано, например, в таблице:
| x 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| x 2 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| x 3 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| y | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
y = 
 x 3 Ú
x 3 Ú  x 2
x 2  Ú x 1
Ú x 1 
 Ú x 1 x 2 x 3 = (x 1 Ú x 2 Ú x 3) (x 1 Ú
Ú x 1 x 2 x 3 = (x 1 Ú x 2 Ú x 3) (x 1 Ú  Ú
Ú  ) (
) ( Ú x 2 Ú
Ú x 2 Ú  ) (
) ( Ú
Ú  Ú x 3).
Ú x 3).
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 13.1. Привести нижеследующие функции к нормальной (безынверсной) форме:
а) Y1 =  .
.
Решение. Применив правило Де Моргана, преобразуем функцию Y 1 к виду
Y1 =  .
.
После применения сочетательного закона можем записать:
Y1 =  .
.
Раскрыв инверсию, получим конъюнктивную нормальную форму (КНФ) исходной функции:
Y1КНФ =  =
=  .
.
Для перехода от КНФ к ДНФ воспользуемся распределительным законом:
Y1ДНФ = ( Ú
Ú  ) (В Ú
) (В Ú  ) =
) =  (В Ú
(В Ú  ) Ú
) Ú  (В Ú
(В Ú  )=
)=  В Ú
В Ú 
 Ú
Ú  В Ú
В Ú 
 =
=  В Ú
В Ú 
 Ú
Ú 
 .
.






