2. Каждому логическому условию должна соответствовать одна стрелка, направленная вверх.
3. Каждому логическому условию всегда соответствует, одна стрелка, направленная вниз.
4. Каждой восходящей (нисходящей) стрелке обязательно соответствует одна нисходящая(восходящая)стрелка.
Пример 10.3. Пусть задана последовательность из n натуральных целых чисел. Составить логическую схему алгоритма нахождения среднего арифметического этих чисел. Тогда данный алгоритм можем записать в виде логической схемы следующего вида:
А0 ¯ 1 A1 q 1 A2 A3 ¯ 2 A4 A5 p 2 A6 A7 Ak,
А0 – начало алгоритма;
А1 – ввод исходной последовательности чисел;
q – проверка логического условия: все ли числа введены;
А2 – задание начального значения для подсчета суммы чисел: S = 0;
А3 – ввод начального значения переменной цикла: i = 1;
А4 – суммирование значений чисел последовательности: S = S + xi;
А5 – увеличение переменной цикла: i = i + 1;
p – проверка логического условия выхода из цикла: i > n;
А6 – нахождение среднего арифметического последовательности чисел: D = S / n;
А7 – вывод найденного значения;
А k – конец работы алгоритма.
Рассмотрим графические схемы алгоритмов (ГСА). Они представляют собой графическую интерпретацию алгоритмов Ляпунова. Приведем основные правила представления графических схем алгоритмов:
· наличие конечного числа вершин;
· наличие одной начальной и одной конечной вершин;
· входы и выходы вершин соединяются между собой с помощью стрелок, направленных от входа к выходу;
· каждый выход соединяется только с одним входом, каждый вход соединяется, по крайней мере, с одним выходом;
· логическое условие имеет некоторое множество входов, но только два выхода («да», «нет»).
Следовательно, оператор начала А0 может иметь только выходящие стрелки (рис. 10.5).

Рис. 10.5. Оператор начала ГСА
Оператор преобразования может иметь входящие и выходящие стрелки (рис. 10.6).

Рис. 10.6. Оператор преобразования ГСА
Логическое условие может иметь много входящих стрелок, выходящих стрелок может быть только две (рис. 10.7)
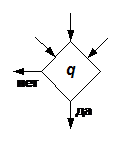
Рис. 10.7. Оператор логического условия
Оператор конца алгоритма имеет только входящие стрелки (рис. 10.8).

Рис. 10.8. Оператор окончания ГСА
Пример 10.4. Пусть задана логическая схема алгоритма следующего вида: А0¯1А1р11А2р22А3¯2А4А5Аk. На основе приведенных правил построим эту схему в виде ГСА (рис. 10.9).
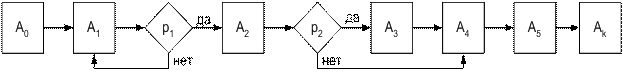
Рис. 10.9. Графическая схема алгоритма (ГСА)
Важной разновидностью графического представления алгоритмов являются структурные схемы алгоритмов (ССА). При такой записи алгоритмов происходит как-бы процесс декомпозиции (т.е. расчленения алгоритма на отдельные этапы - блоки). Блоки изображаются графически в виде геометрических фигур. Каждому блоку присваивается собственный номер. Внутри блока в виде формул или словесно записывается информация, характеризующая выполняемые им функции. Блоки соединяются линиями, символизирующими межблочные связи. Блоки могут описывать элементарные шаги алгоритма или представлять собой части алгоритмов или отдельные алгоритмы.
Правила выполнения структурных схем алгоритмов определены ГОСТом 19.701-90 (ИСО 5807-85) “Схемы алгоритмов, программ, данных и систем. Условные обозначения и правила выполнения”. Фрагмент текста ГОСТа приведен в приложении. Руководствуясь требованиями данного ГОСТа, можно построить структурную схему алгоритма для решения конкретной задачи.
Пример 10.5. Пусть необходимо построить ССА нахождения минимального числа в заданном множестве чисел.
А = { a 1, a 2, a 3, a 4}; |A| = 4 = n, a 1 = 2, a 2 = 1, a 3 = 8, a 4 = 5.
Перед разработкой ССА производится распределение памяти, причем это распределение условное.
Блок «Начало» соответствует началу работы алгоритма.
Блок 1 ввод исходных данных.
Блок 2 задает начальное значение переменной i.
Блок 3 присваивает переменной x значение ai, причем на первом шаге значение ai равно a 1.
Блок 4 сравнивает значение переменной i с n. Это необходимо для определения момента окончания алгоритма.
Блок 5 увеличивает значение переменной i на единицу.
Блок 6 сравнивает предыдущее число ai с последующим ai+1.
Блок 7 печатает значение найденного минимального элемента a 2 = 1.
Блок «Конец» соответствует окончанию работы алгоритма.
На рис. 10.10 приведена структурная схема алгоритма.
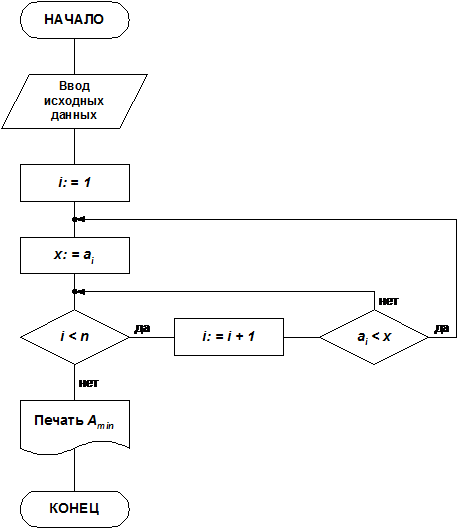
Рис. 10.10. Пример структурной схемы алгоритма
Пример 10.6. Составить алгоритм определения среднего роста студента учебной группы.
Решение:
1. Область допустимых значений исходных данных определена в самом условии задачи и предполагает, что все обрабатываемые значения могут быть только положительными числами (целыми или дробными, в зависимости от принятой единицы измерения).
2. Математическая модель задачи может быть выражена соотношением
 ,
,
где li - рост i -го студента, n - число студентов в учебной группе.
6.3. Составляем структурную схему алгоритма. Вариант структурнойсхемы алгоритма для решения этой задачи показан на рис. 10.11.

Рис.10.11. Вариант структурной схемы алгоритма к примеру 6
Следует отметить, что основа структуры алгоритма представляет собой ограниченный набор стандартных способов соединения базовых блоков для выполнения типичных последовательностей действий. Следовательно, любой алгоритм может быть построен на использовании нескольких базовых блоков путемих комбинации друг с другом на основе связок. Такой подход к разработке алгоритмов называется структурным. К связкам относят:
· следование - последовательное размещение блоков или их групп.
· цикл - структура, определяющая выполнение одного и того же действия несколько раз с различными параметрами вычисляемой величины. Циклическая структура предполагает наличие следующих блоков:
а) присваивание, где происходит задание начальных значений параметров вычисляемой величины;
б) тело цикла, представляющего собой последовательность многократно выполняемых действий;
б) условия выполнение цикла, определяющего выполнение действий в теле цикла или прекращение их выполнения.
Различают два типа циклических структур - цикл "с предусловием" (цикл «до») и цикл "с постусловием" (цикл «пока»). Цикл "до" (рис. 10.12, а) позволяет выполнять заданные действия (тело цикла) несколько раз, до тех пор, пока выполняется некоторое условие. Особенность преобразования информации здесь состоит в том, что цикл «до» выполняется всегда (по крайней мере, один раз), т.к. проверка условия выхода из цикла осуществляется только после выполнения действий. Цикл "пока" (рис. 10.12, б) позволяет выполнить заданные действия только после проверки условия. В этом случае цикл"пока", вотличие от цикла "до", может быть не выполнен ни разу;
· разветвление (рис. 10.13) позволяет выполнять, в зависимости от условия, то илииное действие (или группу действий).
· обход (рис.10.14) представляет собой частный случай разветвления, когда при выполнении (или, наоборот, невыполнении) условия никаких действий не выполняется.
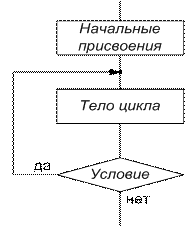

а) цикл «до»; б) цикл «пока»
Рис. 10.12. Типы циклических структур

Рис. 10.13. Структура разветвления
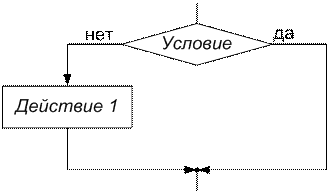
Рис. 10.14. Структура обхода
Особенность приведенных структурных связок состоит в том, что все они имеют единственные вход и выход. Это позволяет просто и наглядно формировать из них в любой последовательности структуру алгоритма. В этой связи, если принять рассмотренные структурные связки за элементарные алгоритмы, алгоритм любой задачи можно представить следующим образом:
АЛГОРИТМ = {<элементарные алгоритмы>}.
Другими словами, алгоритм состоит из набора элементарных алгоритмов. Приведенное определение алгоритма позволяет при разработке алгоритмов сложных задач использовать иерархический подход. Суть данного подхода состоит в следующем: сначала анализируется и записывается структура алгоритма (при этом в полной мере возможно использование описанных выше структурных связок), а затем детализируются отдельные блоки предложенной структуры. Процесс детализации является итерационным, причем уровень детализации с каждой итерацией повышается. Очевидно, что общая структура алгоритма решения задачи может влиять и влияет на результат программной реализации.
Рассмотрим распространенный способ записи алгоритмов – словесное описание. В этом случае алгоритм задается через описание и перечисление операторов, аналогичных блокам, используемым структурной схемой алгоритма. Таким образом, словесная запись алгоритма представляет собой перечень операторов, пронумерованный в порядке их исполнения алгоритмом. При записи условных операторов помимо указания условия, истинность которого необходимо проверить, указываются также номера операторов, которым будет передаваться управление в зависимости от результатов проверки.
Пример 10.7. Приведем словесное описание структурной схемы алгоритма из примера 5.
1. Присвоить переменной i значение, равное 1.
2. Присвоить х значение, равное ai (x — произвольная ячейка памяти).
3. Проверяем, i меньше n или нет. Если меньше, то переходим к п.4, иначе переходим к п.6.
4. Переменной i присвоить значение, равное i + 1.
5. Проверка логического условия ai < x. Если условие выполняется, то переходим к п.2, если нет, то переходим к п.3.
6. Печать минимального числа из множества А.
7. Конец работы алгоритма.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 10.1. Построить логическую схему алгоритма (ЛСА) подсчета арифметического выражения:
.
Решение. Для записи логической схемы алгоритма подсчета данного выражения нами будут использованы следующие операторы:
A 0 - начало программы;
А1 - ввод объема выборки n;
А2 - задание начальных значений переменной цикла i = 0 и промежуточной переменной С = 0;
А3 - оператор увеличения переменной цикла: i = i + 1;
А4 - вычисление значения индекса переменной b: j = n - i + 1;
А5 - вычисление значения произведения: p = ai * bj;
A 6 - суммирование промежуточных значений p: С = С + p;
q - логический оператор проверки условия: i = n;
А7 - вычисление значения исходного выражения: у = С/n;
А k - конец программы.
Ответ: Таким образом, логическая схема алгоритма подсчета данного выражения будет иметь следующий вид:






