Процесс получения обратного преобразования заключается в выделении интегралов, определяемых соотношениями (1.2-5). Напомним здесь эти соотношения:
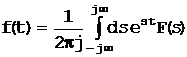(1.1-2)
при обратном преобразовании Фурье;
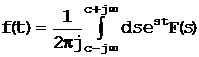(1.2-5)
при обратном преобразовании Лапласа.
В этих соотношениях интегрирование выполняется по всей бесконечной длине мнимой оси в случае преобразования Фурье и по бесконечной линий, параллельной мнимой оси и смещенной так, что все особенности F(s) лежат слева от этой линии, в случае преобразования Лапласа. Вычисление этих интегралов можно упростить, если применить теорему Коши о вычетах. Задача состоит в том, чтобы представить интеграл вдоль всей бесконечной мнимой оси в виде разности между интегралом по замкнутому пути, включающему как мнимую ось, так и дугу полуокружности бесконечного радиуса, и интегралом по полуокружности бесконечного радиуса. Можно показать, что при определенных ограничениях, наложенных на F(s) и t, интеграл на бесконечной полуокружности исчезает и, следовательно, значение интеграла вдоль мнимой оси определяется непосредственно из теоремы о вычетах для замкнутого контура.
Рассмотрим сначала обратное преобразование Фурье. Заметим, что бесконечная полуокружность может быть взята либо в правой либо в левой полуплоскости. Особенности преобразования Фурье F(s) могут в общем случае лежать как в правой, так и в левой полуплоскости. Можно показать, что интеграл по контуру» охватывающему левую полуплоскость, определяет f(t) при t>0, а интеграл по контуру, охватывающему правую полуплоскость определяет f(t) соответственно при t<0. Оба контура показаны на рис. 1.5-1.
Теорема Коши о вычетах устанавливает: "Если С является границей односвязной области (область называют односвязной, если каждый простой замкнутый контур, лежащий целиком внутри области, охватывает только точки самой области и, следовательно, не охватывает граничных точек), внутри которой и на ее границе g(s) аналитична, исключая конечное число полюсов, то значение 
равно произведению 2pj на сумму вычетов в полюсах g(s), лежащих внутри области С".
Остается только вычислить вычеты в каждом из полюсов функции F(s)est, лежащих внутри замкнутого контура. Различным метолам вычисления вычетов в полюсах предпочитается, ввиду его простоты и совершенства, следующий. Вычет в полюсе s=s k порядка m функции g(s) равен
(1.5-11)
Коротко говоря, обратное преобразование Фурье, определяемое соотношением
(1.1-2), может быть вычислено так:
при t<0, (1.5-12)
где суммирование производится по вычетам s k во всех полюсах правой полуплоскости.
Подобным же образом значение f{t) при t>0 можно вычислить, рассматривая контур, полностью охватывающий левую полуплоскость (рис. 1.5-1). Обратное преобразование Фурье при этом дается формулой
при t>0, (1.5-13)
где суммирование производится по вычетам sj во всех полюсах левой полуплоскости.
Пусть, например, требуется определить обратное преобразование Фурье для функции
(1.5-14)
Чтобы определить f{t) при t<0, исследуем полюсы f(t), лежащие в правой полуплоскости. Полюс второго порядка в точке s=a является единственным полюсом в ППП. Воспользовавшись соотношением (1.5-12) при m=2 и s k =a, имеем
при t<0.
Следовательно,
при t<0. (1.5-15)
Чтобы вычислить f(t) при t>0, примем в расчет полюс первого порядка в ЛПП в точке s=—b и воспользуемся соотношением (1.5-13) при m=1.
Отсюда непосредственно следует
при t>0. (1.5-16)
График функции f(t), заданной соотношениями (1.5-15), (1.5-16), показан на рис. 1.5-2. Этим завершается обсуждение преобразования Фурье и его обращения.
