Здесь мы напомним основные определения из теории функций комплексного переменного. Обозначим через F(s) функцию комплексной переменной 
. Говорят, что функция F(s) в области R аналитическая, если в каждой точке области она однозначна и имеет конечную производную. Поэтому если функция F(s) аналитична в точке и некоторой сколь угодно малой окрестности этой точки, то в этой точке F(s) может быть разложена в ряд Тейлора.
Точки, в которых F(s) не аналитична, называются особыми. Особенности функции комплексного переменного важны, поскольку они определяют поведение функции в комплексной плоскости. Аналитическая функция без особенностей является просто постоянной величиной. В особой точке производная F(s) или не существует или зависит от способа стремления к этой точке. Существуют три типа особых точек: полюсы, существенно особые точки и точки ветвления. Особенность при s=a называют полюсом порядка n, если n—наименьшее положительное целое число, такое, что произведение (s—a)nF(s) становится в точке a аналитической функцией. Особую точку a функции F(s) называют существенно особой, если функция F(s) однозначна, ее производная F'(s) не существует и нет такого целого n, для которого при s=a существует производная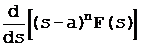 
. Следовательно, существенную особенность можно понимать как полюс бесконечного порядка. Например, функция 
имеет существенную особенность в бесконечности.
Третий тип изолированных особых точек — точки ветвления, которыми обладают многозначные функции. Точка ветвления характеризуется тем, что значение функции после обхода по замкнутому контуру в окрестности точки ветвления будет отличаться от первоначального. Можно показать, что в точке ветвления не существует производных любых порядков. Примером функции, имеющей точки ветвления, является логарифмическая функция 
и степенная функция 
, где k — нецелое число; f(s) в обоих случаях — целая функция, исключая постоянное число. Оба типа этих функций имеют точки ветвления при s=0.
Однозначные аналитические функции можно классифицировать в соответствии с особенностями, которыми они обладают. Функция, с особенностью только в бесконечной точке является аналитической всюду в конечной плоскости и называется целой функцией. Этот тип функций подразделяется далее на целые рациональные и целые трансцендентные функции, соответственно тому, является ли особенность на бесконечности полюсом конечного порядка или существенной особенностью. Целые функции допускают разложение в степенной ряд вида 
, который сходится всюду в конечной части плоскости. Следовательно, целая рациональная функция имеет разложение с конечным числом членов и может быть представлена конечным полиномом от s. Целая трансцендентная функция содержит в своем разложении бесконечное число членов. Примерами целых трансцендентных функций являются sh s, и cos s.
Другим важным и более общим классом является класс таких функций, которые однозначны и не имеют в любой конечной части плоскости других особенностей, кроме полюсов. Функции этого класса называют мероморфными. Из сказанного вытекает, что мероморфная функция является частным двух целых функций и имеет в любой конечной области конечное число полюсов.
Примерами мероморфных функций могут служить sin s/(1— 
), ctg s и G(s)/H{s), где G(s) и H(s) - полиномы от s. Если G(s) и H(s) - конечные полиномы, то функция называется рациональной. Этим завершается рассмотрение классов функций.
