Преобразования Фурье и Лапласа
Приводятся условия, которым должна удовлетворять преобразуемая по Фурье функция f(t). Рассуждения распространяются на специальный случай преобразования Фурье - преобразование Лапласа. Дано (в виде таблицы) перечисление некоторых свойств преобразований Фурье и Лапласа. Рассмотрено обратное преобразование на основе применения теории вычетов. Для иллюстрации приложений обратного преобразования, а также выявления основных ограничений в теории преобразований Фурье и Лапласа, приводится несколько примеров. Наконец, класс преобразуемых по Фурье функций, путем применения множителя, улучшающего сходимость, распространяется на функции единичного скачка и степенные.
Преобразование Фурье; вводные замечания
Пара преобразований Фурье, применяемая далее, определяется соотношениями
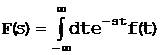, (1.1-1)
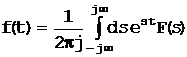, (1.1-2)
где s=jw*). Доказательство того, что выполнение интегральных операций, определяемых соотношениями (1.1-1) и (1-1-2), приводит к исходной функции f(t), представляется очевидным. Подставив функцию F{s) (1.1-1) в (1.1-2) и заменяя в (1.1-2) t на х, приходим в результате к теореме о преобразовании Фурье
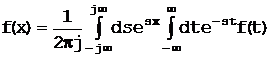. (1.1-3)
Условиями, налагаемыми на f{t) для того, чтобы она была преобразуема по Фурье, являются так называемые условия Дирихле 1—3 для любого конечного интервала t1<t<t2 и условие сходимости 4:
1) функция f{t) может иметь только конечное число разрывов;
2) функция f{t) может иметь только конечное число точек, в которых она обращается в бесконечность;
3) функция f{t) может иметь только конечное число максимумов и минимумов;
4) интеграл 
должен быть сходящимся.
Переход к преобразованию Лапласа
Требование сходимости интеграла накладывает на класс преобразуемых по Фурье функций определенное ограничение. Такие употребительные в технике функции, как функция единичного скачка, линейная функция или периодическое колебание, в строгом смысле не являются преобразуемыми по Фурье. Если несколько ослабить требование сходимости путем введения экспоненциального множителя, обеспечивающего сходимость, то класс преобразуемых функций существенно расширится. В этом плане покажем, что преобразование Лапласа является специальным случаем преобразования Фурье.
*) Вообще переменная s используется в качестве комплексной переменной s+jw. Однако в прямом преобразовании Фурье переменная s понимается только как мнимая часть, т. е. s=jw.
Предположим, что шкала времени выбрана так, что функция f(t) представляет интерес только при t>0; кроме того, введем множитель е-st. Тогда условие сходимости, которому должна удовлетворять функция f(t), будет следующим:
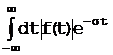сходится. (1.2-1)
Нижняя граница множества чисел s, обеспечивающих сходимость интеграла, называется абсциссой абсолютной сходимости и обозначается через sa. Теорема о преобразовании Фурье дает:
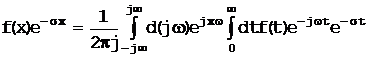. (1.2-2)
Умножая обе части этого соотношения на 
и заменяя переменную интегрирования s=jw на s+jw, получим
. (1.2-3)
Чтобы обеспечить теперь выполнение условия сходимости при интегрировании по переменной 
, ее действительная часть должна быть больше чем sa. Обозначим это значение s>sa через с. Мы можем, далее, рассматривать как комплексную переменную и заменить ее на s. Отсюда непосредственно следует
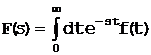(1.2-4)
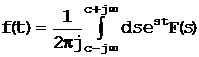(1.2-5)
где s= 
и с >sa.
Эти два уравнения составляют прямое и обратное преобразования Лапласа.
