Тема 12. Окружность и круг

Автор статьи [2, C.27] А. Малеев в шутливой форме так поясняет принцип Дирихле: «Если шесть зайцев посадить в пять клеток, то обязательно найдется клетка, в которой будут сидеть не менее двух зайцев» (При этом, естественно, подразумевается, что целостность зайцев не нарушается).

Существует много задач, при решении которых используется именно принцип Дирихле.

Задания:

№1. В ящике лежит сотня флажков: красные, зеленые, желтые и синие –поровну. Какое наименьшее число флажков нужно взять не глядя, чтобы среди них обязательно было не меньше десяти флажков одного цвета (безразлично какого)?

№2. В одном ящике лежит 10 пар коричневых и 10 пар черных носков, а в другом – 10 пар коричневых и 10 пар черных перчаток. Из них, не глядя, вынимают несколько носков и несколько перчаток. Какое наименьшее число носков и перчаток надо извлечь из этих ящиков, чтобы из них можно было составить пару одноцветных носков и пару одноцветных перчаток (все носки и все перчатки одного размера)?

№3. В ящике лежит 40 шаров различного цвета: 17 зеленых, 12 синих, 5 красных, остальные 6 шаров окрашены в белый и черный цвета. Какое наименьшее число шаров нужно вынуть, не заглядывая в ящик, чтобы среди вытянутых шаров оказалось: а) не менее 6 шаров одного цвета; б) хотя бы один зеленый шар; в) хотя бы 2 синих шара?

№4. В одном классе 23 ученика Можно ли утверждать, что в этом классе найдутся хотя бы два ученика, фамилии которых начинаются с одной и той же буквы? А если бы в этом классе было 35 учеников?

№5. В ящике комода хранятся красные, желтые и зеленые носки. Какое наименьшее число носков надо взять наугад из комода, чтобы среди них обязательно оказались четыре носка одного цвета?

№6. Три поросенка, Ниф-Ниф, Нуф-Нуф и Наф-Наф, хранят в жестяной коробке красные, желтые и зеленые леденцы. Какое наименьшее число
леденцов надо взять наугад из коробки, чтобы
каждому поросенку обязательно достались пять леденцов одного цвета.

№7.  В темном чулане N гномов хранят вперемежку колпаки разных цветов, причем колпаков каждого цвета поровну. Проснувшись как-то
утром, первый гном попросил m₁  колпаков одного цвета. Белоснежка сходила в чулан и отсчитала в темноте наугад несколько колпаков, чтобы их
наверняка хватило выполнить его просьбу. Но тут проснулись остальные гномы, и второй гном
попросил m₂  колпаков одного цвета, третий m₃  колпаков и так далее, вплоть до последнего гнома, который попросил m_n колпаков одного цвета, причем m₁³ m₂³ m₂³…³ m_n.Чтобы выполнить просьбы всех гномов, Белоснежка вынуждена была еще раз сходить в чулан. Какое наибольшее количество цветов могли иметь колпаки, хранящиеся в темном чулане?

Замечание: 1. Если задача вызывает затруднение, то попробуй решить её сначала на конкретных числах.

2. Если же решение задачи совсем не получается, то изучи её решение, представленное в  статье   [2].

После выполнения всех заданий напиши реферат по теме «Принцип Дирихле».

Литература:

1. Депман И.Я., Виленкин Н.Я. За страницами учебника математики: Пособие для учащихся 5-6 кл. сред. шк. –М.: Просвещение, 1989. С.229-230.

2. Малеев А. О колпаках, хранящихся в темных
чуланах // Квант.-2003.№2. С. 27-30.

Тема 14. Положительные и отрицательные
целые числа

Отрицательные числа возникли примерно во II веке до н.э. Ввели это понятие китайские ученые. Они рассматривали понятие отрицательного числа как долг и обозначали чернилами другого цвета. Позднее отрицательные числа встречаются в трудах индийских математиков, которые ставят над этими числами точку. Например, число минус три записывали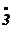  

Древнегреческий математик Диофант (3 век н.э.) при решении уравнений фактически уже пользовался правилом умножения отрицательных чисел, формулируемое так: «Вычитаемое, умноженное на прибавляемое, дает в результате вычитаемое; вычитаемое на вычитаемое дает прибавляемое».

Известно также из истории математики, что
правило умножения положительных и отрицательных чисел было введено впервые индийскими учеными, которые трактовали отрицательные
числа с долгом, а положительные числа с имуществом (7 в.).

Итальянский математик Леонардо Фибоначчи (12-13 вв.) пришел к мысли, что отрицательные количества надо понимать в смыcле противоположном положительным. Немецкий математик Михаил Штифель впервые в 1544 г. дал определение отрицательных чисел как чисел, меньших
нуля. Великий французский математик Рене
Декарт (1596-1650) предложил откладывать отрицательные числа на координатной прямой влево от нуля. Всеобщее признание отрицательные числа получили в первой половине 19 века. Тогда же появилась современная запись отрицательных
чисел.

Задания:

№1. Познакомься с историей возникновения и развития отрицательных чисел в математике.

№2. Установи причины возникновения отрицательных чисел в математике.

№3. Записать в клетках квадрата 3х3 числа -1, +2,
-3, +4, -5, +6, -7, +8, -9 так, чтобы их произведения по всем горизонталям, вертикалям, диагоналям были отрицательными.

№4. Даны 173 числа, каждое из которых равно 1 или -1. Можно ли разбить их на две группы так, чтобы суммы чисел, входящих в каждую группу, были бы равны?

№5. Можно ли написать подряд 17 различных
целых чисел так. чтобы произведение любых
четырех соседних чисел было отрицательным, а произведение всех чисел положительным? Привести пример.

№6. Даны 1989 положительных чисел. Известно, что произведение любых 22 из них больше 1.
Докажи, что произведение всех данных чисел больше 1. 

После выполнения всех заданий напиши реферат по теме «Положительные и отрицательные целые числа».

Литература:

1. Глейзер Г.И. История математики а в школе.
IV –VI классы: Пособие для учителей. – М.:
Просвещение, 1981. С. 61-65.

2. Депман И.Я., Виленкин Н.Я. За страницами учебника математики: Пособие для учащихся 5-6 кл. сред. шк. –М.: Просвещение, 1989. С.76-77.

3. Утеева Р.А. Дифференцированные задания по математике. 6 класс: Пособие для учителя. –Тольятти, 1996. Задания № 3. С. 14-17.

Приложение 1

Образец оформления титульного листа