1. Если L: 
, 
– кусочно-гладкая кривая в R3, то ее длина s может быть найдена по формуле 
а, если кривая в R2, то 
.
2.Пусть L – материальная плоская кривая с линейной плотностью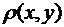 
или пространственная кривая с линейной плотностью 
. Тогда для нахождения массы кривой можно использовать криволинейный интеграл первого рода m = 
.
3. Пусть в каждой точке области G пространства R3 задана вектор-функция 
. Тогда говорят, что задано силовое поле 
.
Криволинейный интеграл второго рода используют для нахождения работы A силового поля 
при перемещении вдоль кривой ГAB: A= 
4. Если в формуле Грина положить Q=x, P=0 и учесть, что 
равен площади S области G, то получим выражение площади плоской фигуры через криволинейный интеграл:
S= 
. Если взять в качестве Q=0, P=-y, выражение для S примет вид S= 
.
Для вычисления площади используют также формулу
S= 
.
Задача 16. 1. Найти длину дуги плоской кривой y=ln cos x, 
.
Решение. Запишем параметрические уравнения кривой в виде: x=x, y=ln cos x, . Тогда 
= = 
= 
= = 
.
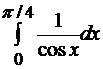Задача 16. 2. Найти длину дуги пространственной кривой 
.
Решение. Для применения формулы вычисления длины кривой необходимо вычислить производные 
. Далее подставляя в формулу 
получим s= 
.
Задача 16. 3. Найти массу, распределенную с линейной плотностью по дуге плоской кривой ГAB: y=x2/2, A(1; 1,5) B(2; 2); 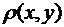=y/x.
Решение. Здесь мы должны воспользоваться формулой
m = 
. Вспомнив, что дифференциал дуги вычисляется по формуле ds= 
, а переменная x меняется от 1 до 2, окончательно получим m = 
= 
.
Задача 16. 4. Найти массу, распределенную с линейной плотностью по дуге пространственной кривой Г: x=at, y=at2/2, z= at3/3; 
; 
.
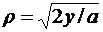Решение. Массу кривой будем находить по формуле m= 
== 
= = 
.
Задача 16. 5. Найти площадь области, ограниченной плоской кривой y2= 4- x, x=4, y=1.
Решение. Область, площадь которой нужно найти, представляет собой криволинейный треугольник ABC, где A(
), B(4; 1)C(4;0). Граница области образована AC: y2= 4- x, 
CB: x=4,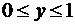 
, BA: y=1, . Для вычисления площади будем использовать формулу S= 
= 
= 1/3.
Рассмотрим, например, как вычисляется интеграл I= 
. На CB x= 4, поэтому dx=0, а y меняется от 0 до 1. Поэтому I= 
= 
=4.
Задача 16. 6. Найти работу поля = {z, -x, y} вдоль кривой AB, если AB – виток винтовой линии x=acos t; y= bsin t; z=ct; 
; A(a;0;0), B(a;0;2 
).
Решение. Запишем формулу вычисления работы A= , где ={P;Q;R}. В данном примере 
, дифференциалы 
. Подставим в интеграл 
= 
= = 
= = 
= = 
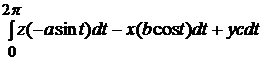+0= 
= 
.
Условие независимости криволинейного интеграла второго рода от пути интегрирования. Область G на плоскости называется односвязной, если для любого замкнутого контура, лежащего в этой области, ограниченная им часть плоскости целиком принадлежит области G.
Если функции P и Q непрерывны в односвязной области G. Тогда криволинейный интеграл 
не зависит от пути интегрирования ГAB (ГAB – кривая, лежащая в области, точка A – ее начало, точка B - конец) тогда и только тогда, когда выражение 
является полным дифференциалом некоторой функции u=u(x, y), т.е. в области G выполняется условие du= Pdx+Qdy, или 
=P, 
= Q. При этом для любой кривой ГAB, лежащей в области, имеет место равенство = u(B) – u(A).
Пусть функции P, Q, 
, 
непрерывны в односвязной области G. Для того чтобы криволинейный интеграл не зависел от пути интегрирования, необходимо и достаточно, чтобы в G выполнялось условие 
= 
.
Задача 16. 7. Найти работу поля = {y, x} от точки A(1;0) до точки B(-4;3).
Решение. Поскольку в интеграле 
выражение 
является полным дифференциалом (действительно = =1), то значение интеграла не зависит от пути интегрирования ГAB. Поэтому в качестве ГAB мы можем выбрать ломаную AMB, где точка M(1; 3). Тогда AM={x=1, 
}, BM=={y=3, 
}. Интеграл 
= 
= 
= 
=-12.
Задача 16. 8. Доказать, что подынтегральное выражение является полным дифференциалом, и вычислить криволинейный интеграл 
, где A(-2;-1), B(3;0).
Решение. Нужно проверить выполнение условия = . Затем выбрать удобный путь интегрирования и вычислить криволинейный интеграл: I= 62.
Задания для самостоятельной работы:
Задача 16. 9. Найти длину дуги плоской кривой ay2= x3, 
. Ответ: 335a/27.
Задача 16.10. Найти длину дуги пространственной кривой 
, 
. Ответ: 5.
Задача 16. 11. Найти массу, распределенную с линейной плотностью по дуге пространственной кривой Г: x=tcost, y=tsint, z= t; 
; 
.
Ответ: 
.
Задача 16. 12. Найти площадь области, ограниченной кривыми
y= 1- x2, x – y – 1 =0. Ответ: 9/2.
Задача 16. 13. Доказать, что подынтегральное выражение является полным дифференциалом, и вычислить криволинейный интеграл 
, где A(3;0), B(0;-3).
Ответ: 0.
Задача 16. 14. Найти работу поля = 
вдоль дуги AB кривой Г, где A(1;0), B(0;1), если:
1) Г – ломаная APB, где P(1;1);
2) Г- четверть окружности 
;
3) Г- четверть астроиды 
.
Ответ: 1), 2),3) 
