Пусть плоская спрямляемая кривая С задана уравнениями
x =x(s), y =y(s), 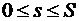 , где s – длина дуги этой кривой от некоторой ее точки M0 до точки M(x, y). Значение s=0 соответствует начальной точке M0. На кривой задана непрерывная функция f.
, где s – длина дуги этой кривой от некоторой ее точки M0 до точки M(x, y). Значение s=0 соответствует начальной точке M0. На кривой задана непрерывная функция f.
Число 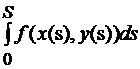 называют криволинейным интегралом первого рода от функции f по кривой C. Обозначают такой интеграл
называют криволинейным интегралом первого рода от функции f по кривой C. Обозначают такой интеграл 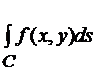 . Криволинейные интегралы первого типа обладают свойствами, аналогичными свойствам определенного интеграла Римана: линейность, аддитивность.
. Криволинейные интегралы первого типа обладают свойствами, аналогичными свойствам определенного интеграла Римана: линейность, аддитивность.
Если на плоскости xy кривая С задана уравнениями x= 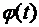 , y=
, y= 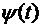 ,
, 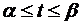 , где функции
, где функции 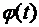 ,
, 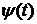 - непрерывны на
- непрерывны на  и имеют непрерывные производные
и имеют непрерывные производные 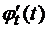 ,
, 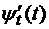 , не обращающиеся в нуль одновременно. Тогда справедлива формула вычисления криволинейного интеграла первого рода
, не обращающиеся в нуль одновременно. Тогда справедлива формула вычисления криволинейного интеграла первого рода
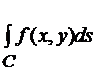 =
= 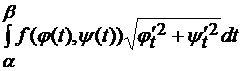 (1.16)
(1.16)
Сделаем несколько замечаний.
1. Если кривая С задана уравнением y=y(x), 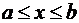 , и функция y(x) имеет непрерывную производную на [a,b], то справедлива следующая формула вычисления криволинейного интеграла первого рода
, и функция y(x) имеет непрерывную производную на [a,b], то справедлива следующая формула вычисления криволинейного интеграла первого рода
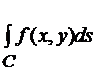 =
= 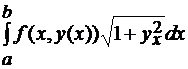 . (2.16)
. (2.16)
2. Если кривая С задана в полярных координатах уравнением 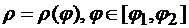 , и функция
, и функция 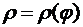 имеет непрерывную производную на
имеет непрерывную производную на 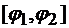 , то криволинейный интеграл первого рода может быть вычислен по формуле
, то криволинейный интеграл первого рода может быть вычислен по формуле
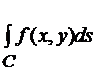 =
= 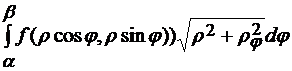 . (3.16)
. (3.16)
3. Для гладкой пространственной кривой С, заданной уравнениями x= 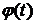 , y=
, y= 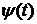 , z=
, z= 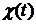
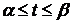 , справедлива формула
, справедлива формула 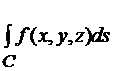 =
= 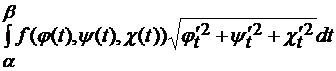 (4.16)
(4.16)
Задача 15.1. Вычислить криволинейный интеграл: 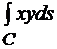 , где С - четверть эллипса
, где С - четверть эллипса 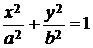 ,лежащая в первом квадранте.
,лежащая в первом квадранте.
Решение. Как можно получить параметрические уравнения эллипса? Изменим немного формулы перехода к полярным координатам 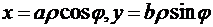 и подставим эти выражения в уравнение эллипса. Получим
и подставим эти выражения в уравнение эллипса. Получим 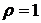 . С учетом условия задачи про четверть эллипса, лежащую в первом квадранте параметрические уравнения эллипса запишем в виде: x=acos t, y=bsin t,
. С учетом условия задачи про четверть эллипса, лежащую в первом квадранте параметрические уравнения эллипса запишем в виде: x=acos t, y=bsin t, 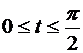 .
.
Найдем производные x’= - a sin t, y’= bcos t. Подставим найденные значения в формулу (1.16).
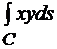 =
= 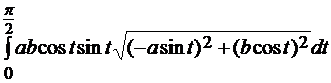 = =
= = 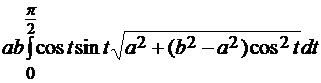 = =
= = 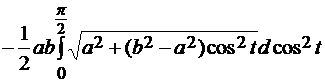 = =
= = 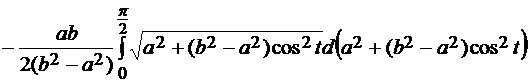 = =
= = 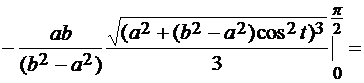
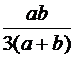 .
.
Задача 15.2. Вычислить криволинейный интеграл: 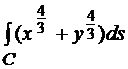 , где кривая С – астроида
, где кривая С – астроида 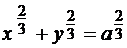 .
.
Решение. Чтобы получить параметрические уравнения астроиды, следует воспользоваться обобщенными полярными координатами: 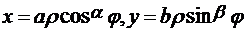 , где
, где 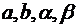 специальным образом подобранные постоянные. В данном случае
специальным образом подобранные постоянные. В данном случае 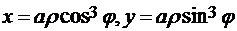 . Подставим эти выражения в уравнение астроиды, получим
. Подставим эти выражения в уравнение астроиды, получим 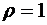 . Окончательно, параметрические уравнения астроиды
. Окончательно, параметрические уравнения астроиды 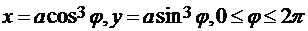 . После всех вычислений получим
. После всех вычислений получим 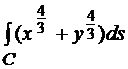 =
= 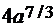 .
.
Задача 15.3. Вычислить криволинейный интеграл: 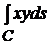 , где кривая С – граница прямоугольника (0, 0), (4, 0), (4, 2), (0, 2).
, где кривая С – граница прямоугольника (0, 0), (4, 0), (4, 2), (0, 2).
Ответ. 24
Задача 15.4. Вычислить криволинейный интеграл: 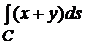 , где кривая С – правый лепесток лемнискаты, заданной в полярных координатах уравнением
, где кривая С – правый лепесток лемнискаты, заданной в полярных координатах уравнением 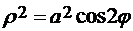 .
.
Ответ..
Криволинейный интеграл второго рода. Кривая AB задана уравнениями x= 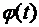 , y=
, y= 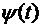 ,
, 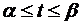 . Здесь A=A(
. Здесь A=A(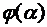 ,
, 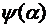 ) B= B(
) B= B(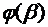 ,
, 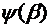 ). Функции P=P(x, y) и Q=Q(x, y) определены и непрерывны на кривой AB. Пусть
). Функции P=P(x, y) и Q=Q(x, y) определены и непрерывны на кривой AB. Пусть 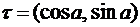 - единичный касательный вектор к кривой AB в точке M(x, y),
- единичный касательный вектор к кривой AB в точке M(x, y), 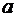 - угол, между вектором
- угол, между вектором 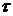 в точке M(x, y) и осью Ox. Тогда криволинейный интеграл второго рода
в точке M(x, y) и осью Ox. Тогда криволинейный интеграл второго рода 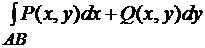 =
= 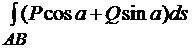 .
.
Если AB – гладкая кривая, то вычислить криволинейный интеграл второго рода можно по формуле 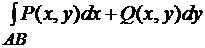 = =
= = 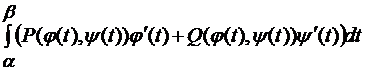 . (5.16)
. (5.16)
Если кривая С задана уравнением y=y(x), 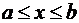 , и функция y(x) имеет непрерывную производную на [a,b], то справедлива следующая формула вычисления криволинейного интеграла второго рода
, и функция y(x) имеет непрерывную производную на [a,b], то справедлива следующая формула вычисления криволинейного интеграла второго рода
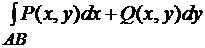 =
= 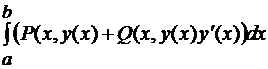 . (6.16)
. (6.16)
Если C - гладкая кривая в R3, заданная уравнениями x=  , y=
, y= 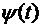 , z=
, z= 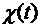 ,
, 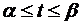 , то
, то 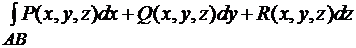 =
= 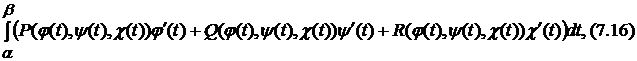
Задача 15.5. Вычислить криволинейный интеграл: 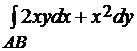 , где кривая AB – кривая, соединяющая точки A(0; 0), B(1; 1) с уравнением y= x2.
, где кривая AB – кривая, соединяющая точки A(0; 0), B(1; 1) с уравнением y= x2.
Решение. Кривая задана уравнениемy= x2 и производная y’=2x. По формуле (6.16) получим
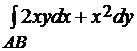 =
= 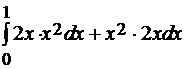 =
= 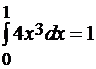 .
.
Задача 15.6. Вычислить криволинейный интеграл по отрезку AB, A(3; -4), B(1; 2): 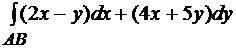 .
.
Решение. Уравнение прямой AB имеет вид 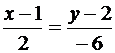 . Отсюда y= -3x +5. По формуле (6.16) получим
. Отсюда y= -3x +5. По формуле (6.16) получим
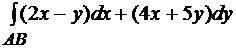
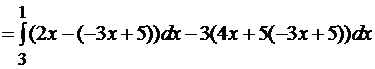 =
= 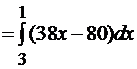
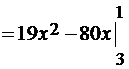 =8.
=8.
Задача 15.7. Вычислить криволинейный интеграл второго рода 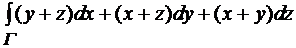 по пространственной кривой Г:
по пространственной кривой Г: 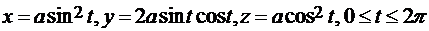 .
.
Решение. Для применения формулы (5.16) вычислим производные переменных x, y, z по t.
Получим 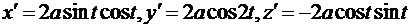 .
.
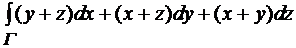 = =
= = 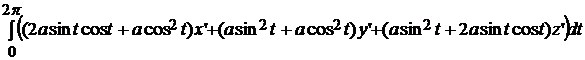 =
=
= 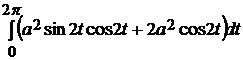 =
= 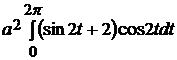 =
= 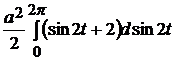 =0.
=0.
Задача 15.8. Вычислить криволинейный интеграл второго рода 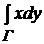 по кривой Г, пробегаемой от точки A к точке B: Г – полуокружность x2+y2=a2,
по кривой Г, пробегаемой от точки A к точке B: Г – полуокружность x2+y2=a2,  , A(0;-a), B(0;a).
, A(0;-a), B(0;a).
Решение. Здесь можно, выразив переменную y как функцию от x, вычислить интеграл,
используя формулу (6.16). Однако удобнее перейти к полярным координатам и получить параметрические уравнения кривой. Подставим  в уравнение окружности. Таким образом, нас интересуют те и только те точки плоскости, у которых
в уравнение окружности. Таким образом, нас интересуют те и только те точки плоскости, у которых  . Значит, параметрические уравнения окружности имеют вид
. Значит, параметрические уравнения окружности имеют вид 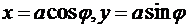 . Параметр
. Параметр  изменяется от
изменяется от 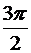 (точка A) до
(точка A) до 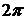 (точка B). Далее следует вычисление интеграла по формуле (5.16):
(точка B). Далее следует вычисление интеграла по формуле (5.16):
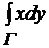 =
= 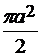 .
.
Формула Грина. Пусть граница Г плоской ограниченной области G состоит из конечного набора кусочно-гладких кривых. Тогда, если функции P, Q,  ,
,  непрерывны на
непрерывны на 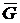 , то справедлива формула Грина
, то справедлива формула Грина 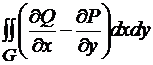 =
= 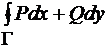 , где контур Г ориентирован так, что при его обходе область G остается слева.
, где контур Г ориентирован так, что при его обходе область G остается слева.
Задача 15.9. Вычислить криволинейные интегралы 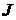 с помощью формулы Грина
с помощью формулы Грина
1) 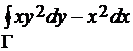 , где Г - окружность
, где Г - окружность 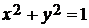 ;
;
2) 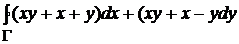 , где Г - эллипс
, где Г - эллипс 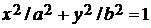 .
.
Решение. По формуле Грина 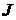 =
= 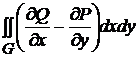 .
.
В задании 1) функции P= -x2, Q = xy2. Отсюда 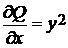 ,
, 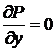 .
.
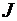 =
= 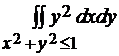 . Далее, имеет смысл перейти к полярной системе координат и записать
. Далее, имеет смысл перейти к полярной системе координат и записать 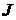 в виде
в виде 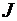 =
= 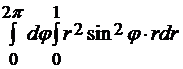 =
= 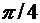 .
.
Задания для самостоятельной работы:
Задача 15.10. Вычислить криволинейный интеграл: 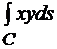 , где С – граница квадрата с вершинами (1;0), (0;1), (-1;0), (0;-1). Ответ: 0
, где С – граница квадрата с вершинами (1;0), (0;1), (-1;0), (0;-1). Ответ: 0






