Основные понятия. Пусть z = z(x, y); (x, y) 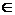 G – непрерывная функция двух переменных. График этой функции, т.е. множество точек вид {x, y, z(x, y)│ (x, y)
G – непрерывная функция двух переменных. График этой функции, т.е. множество точек вид {x, y, z(x, y)│ (x, y) 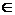 G } – поверхность в пространстве
G } – поверхность в пространстве  . Это явное уравнение поверхности. Оно может быть также записано в виде y = y(x, z) или x = x(y, z).
. Это явное уравнение поверхности. Оно может быть также записано в виде y = y(x, z) или x = x(y, z).
Поверхность может быть задана параметрически
x=  (u, v), y=
(u, v), y=  (u, v), z=
(u, v), z=  (u, v), (u, v)
(u, v), (u, v)  , (1.18)
, (1.18)
где  ,
,  ,
,  - непрерывные функции в области
- непрерывные функции в области  . Каждой точке (u, v)
. Каждой точке (u, v)  ставится в соответствие точка (x, y, z) пространства
ставится в соответствие точка (x, y, z) пространства  , образующих поверхность. В принципе, случай явного задания поверхности легко может быть сведен к параметрическому:
, образующих поверхность. В принципе, случай явного задания поверхности легко может быть сведен к параметрическому:  , (x, y)
, (x, y) 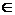 G.
G.
В дальнейшем, мы будем считать, что область 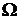 замкнута и ограничена, а функции
замкнута и ограничена, а функции  ,
,  ,
,  непрерывно дифференцируемы.
непрерывно дифференцируемы.
Пусть  - некоторая точка поверхности S. Рассмотрим векторы
- некоторая точка поверхности S. Рассмотрим векторы  ,
,  , вычисленные в точке M0. Точку будем называть неособой, если эти векторы линейно независимы, и особой в противном случае.
, вычисленные в точке M0. Точку будем называть неособой, если эти векторы линейно независимы, и особой в противном случае.
Итак, мы рассматриваем поверхность S, заданную параметрическими уравнениями (1.18), не имеющую особых точек.
Площадь такой поверхности может быть вычислена по формуле  , где A=
, где A= 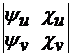 ; B=
; B= 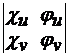 ; C=
; C=  . Здесь через
. Здесь через  обозначены соответствующие частные производные этих функций по u, v.
обозначены соответствующие частные производные этих функций по u, v.
Замечание. Введем в рассмотрения функции E=  ; G=
; G=  ; F=
; F= 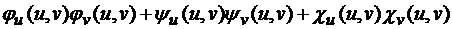 . Справедливо равенство A2+B2+C2=EG-F2. Тогда формулу для вычисления площади поверхности можно переписать в виде
. Справедливо равенство A2+B2+C2=EG-F2. Тогда формулу для вычисления площади поверхности можно переписать в виде  .
.
Поверхностные интегралы первого рода. Определение поверхностного интеграла первого рода как предела интегральных сумм может быть сформулировано стандартным образом. Однако нас сейчас интересует его вычисление. Поэтому приведем здесь формулу для вычисления.
Пусть на поверхности S определена функция f(M)=f(x, y, z).
Поверхностный интеграл первого рода  равен двойному интегралу
равен двойному интегралу  =
= 
или  =
=  . (2.18)
. (2.18)
Если поверхность задана явно, т.е. z = z(x, y); (x, y)  G, то
G, то  =
=  , (3.18)
, (3.18)
где через  и
и  обозначены частные производные функции z по x и y соответственно.
обозначены частные производные функции z по x и y соответственно.
Задача 17.1. Вычислить 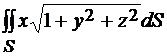 , где S - часть параболоида
, где S - часть параболоида 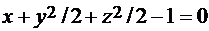 , отсечённая плоскостью х = 0.
, отсечённая плоскостью х = 0.
Решение. Уравнение поверхности удобно переписать в виде
x=f(y, z), т. к. все точки параболоида однозначно проектируются в точки круга плоскости yz. Заметим, что на другие координатные плоскости будет проектироваться по две половины параболоида.
Для вычисления будем использовать формулу вида (3.18). Для данного интеграла ее следует записать в виде  = =
= =  .
.
Вычислим элемент dS поверхности x=1-y2-z2. Запишем формулу в общем виде и получим для данной поверхности  .
.
Множество G - это круг  в плоскости yz. Функцию f(x, y, z) выразим через выбранные переменные y, z, т.е.
в плоскости yz. Функцию f(x, y, z) выразим через выбранные переменные y, z, т.е.  .
.
Запишем поверхностный интеграл через двойной по области G:  = =
= =  .
.
Для вычисления двойного интеграла используем переход к полярной системе координат: 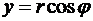 ,
,  , якобиан
, якобиан  ). Ответ:
). Ответ: 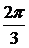 .
.
Задача 17.2. Вычислить значение интеграла  , S - поверхность конуса
, S - поверхность конуса  .
.
Решение. Здесь, как и в предыдущей задаче, речь идет о поверхности, заданной в явном виде:  . Область G изменения переменных (x,y) получена в результате проектирования поверхности S на координатную плоскость xy (проектирование должно быть взаимно однозначным). Поэтому область G определяется условием
. Область G изменения переменных (x,y) получена в результате проектирования поверхности S на координатную плоскость xy (проектирование должно быть взаимно однозначным). Поэтому область G определяется условием  . Подынтегральная функция здесь уже представлена как функция, зависящая от переменных x,y. Ответ:
. Подынтегральная функция здесь уже представлена как функция, зависящая от переменных x,y. Ответ:  .
.
Задача 17.3. Вычислить значение интеграла  , S – поверхность x= ucosv, y=usinv, z=v,
, S – поверхность x= ucosv, y=usinv, z=v,  .
.
Решение. Здесь речь идет о поверхности, заданной в параметрическом виде. Для вычисления будем использовать формулу (2.18), причем здесь  .
.  =
=  =
=  =
=  .
.
Задача 17.4. Найти площадь полусферы радиуса 5.
Решение. Запишем параметрические уравнения сферы x2+y2+z2 =52,  . Перейдем к сферическим координатам и получим, что точки сферы в этой системе координат задаются условием R=5. Тогда параметрическое представление сферы
. Перейдем к сферическим координатам и получим, что точки сферы в этой системе координат задаются условием R=5. Тогда параметрическое представление сферы  ,
,  ,
,  , где
, где 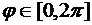 ,
,  . Вычислим дифференциальный элемент площади
. Вычислим дифференциальный элемент площади  и найдем площадь полусферы по формуле
и найдем площадь полусферы по формуле  = =
= =  . В ответе получим
. В ответе получим  .
.
В качестве приложения поверхностного интеграла первого рода к решению физических задач рассмотрим формулу нахождения массы поверхности. Пусть S – материальная поверхность с поверхностной плотностью  в точке M(x, y, z). Тогда массу поверхности мы можем определить по формуле M=
в точке M(x, y, z). Тогда массу поверхности мы можем определить по формуле M=  . Эту формулу мы будем использовать для решения следующей задачи.
. Эту формулу мы будем использовать для решения следующей задачи.
Задача 17.5. Вычислить массу цилиндрической поверхности  , отсечённой плоскостями х =0, х =4, если плотность в каждой её точке есть функция
, отсечённой плоскостями х =0, х =4, если плотность в каждой её точке есть функция 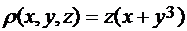 .
.
Решение. Построим поверхность. Учтем, что поверхность задана в явном виде и выберем координатную плоскость для проектирования. Необходимо продумать, какими соображениями будем руководствоваться по этому поводу и нарисовать проекцию поверхности на координатную плоскость. Вычислим элемент dS поверхности. Составим поверхностный интеграл  и вычислим его, сводя к двойному. В ответе получим 16.
и вычислим его, сводя к двойному. В ответе получим 16.
Поверхностные интегралы второго рода. Пусть поверхность S задана параметрически x=  (u, v), y=
(u, v), y=  (u, v), z=
(u, v), z=  (u, v), (u, v)
(u, v), (u, v)  , функции
, функции  (u, v),
(u, v),  (u, v),
(u, v),  (u, v) непрерывно дифференцируемы в
(u, v) непрерывно дифференцируемы в 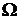 , причем векторы
, причем векторы  и
и 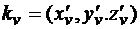 неколлинеарны. В каждой точке такой поверхности существуют два противоположно направленных нормальных вектора. Выбор одного из этих направлений означает выбор стороны поверхности. В качестве вектора нормали можно выбрать
неколлинеарны. В каждой точке такой поверхности существуют два противоположно направленных нормальных вектора. Выбор одного из этих направлений означает выбор стороны поверхности. В качестве вектора нормали можно выбрать  , где M – точка поверхности. Его координаты
, где M – точка поверхности. Его координаты  . Обозначим их через {A; B; C} соответственно. Если поверхность задана уравнением z=f(x; y; z), то вектор нормали определяется как
. Обозначим их через {A; B; C} соответственно. Если поверхность задана уравнением z=f(x; y; z), то вектор нормали определяется как  .
.
Будем считать, что мы выбрали одну из сторон поверхности S. Пусть  - углы, которые вектор
- углы, которые вектор 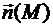 составляет с осями координат, и пусть на поверхности заданы три функции P(M), Q(M), R(M).
составляет с осями координат, и пусть на поверхности заданы три функции P(M), Q(M), R(M).
Поверхностные интегралы второго рода определяются через интегралы первого рода 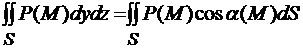 ,
,  ,
,  . Используя формулы сведения поверхностного интеграла первого рода к двойному, мы можем получить формулу для вычисления
. Используя формулы сведения поверхностного интеграла первого рода к двойному, мы можем получить формулу для вычисления  =
=  . (4.18)
. (4.18)
Если поверхность S задана уравнением z=f(x, y), (x, y)  и выбрана верхняя сторона поверхности (это означает, что
и выбрана верхняя сторона поверхности (это означает, что  ),
),
тогда  =
=  . Аналогично могут быть записаны формулы для вычисления интегралов
. Аналогично могут быть записаны формулы для вычисления интегралов  ,
,  , если поверхность S задана уравнением x=x(y, z), (y,z)
, если поверхность S задана уравнением x=x(y, z), (y,z)  и уравнением y=y(z, x), (z, x)
и уравнением y=y(z, x), (z, x)  соответственно.
соответственно.
Задача18.6. Вычислить  , где S - внешняя сторона замкнутой поверхности
, где S - внешняя сторона замкнутой поверхности 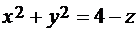 , z=0.
, z=0.
Решение. Поверхность S состоит из поверхности параболоида П: 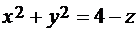 ,
,  , причем выбрана верхняя сторона, и нижней части плоскости z=0, выделяемой условием К:
, причем выбрана верхняя сторона, и нижней части плоскости z=0, выделяемой условием К: 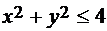 . Будемвычислять каждый из интегралов
. Будемвычислять каждый из интегралов  ,
, 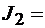
 ,
, 
 отдельно.
отдельно.
Рассмотрим первое слагаемое  . Понятно, что
. Понятно, что  , где S1 - половина параболоида, описываемая уравнением
, где S1 - половина параболоида, описываемая уравнением  , соответствующая нормаль
, соответствующая нормаль 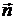 образует острый угол с осью O х, S2 - часть параболоида с уравнением
образует острый угол с осью O х, S2 - часть параболоида с уравнением  , косинус угла, составленного нормалью к этой половине параболоида и осью Ox, отрицательный. Обе части S1 и S2 проектируются на область
, косинус угла, составленного нормалью к этой половине параболоида и осью Ox, отрицательный. Обе части S1 и S2 проектируются на область  плоскости yz, граница которой состоит из дуги параболы
плоскости yz, граница которой состоит из дуги параболы 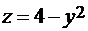 и отрезка оси Oy
и отрезка оси Oy 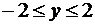 . Поверхностные интегралы по S1 и S2 сведем к двойным интегралам по области
. Поверхностные интегралы по S1 и S2 сведем к двойным интегралам по области  . Получим
. Получим
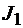 =
= 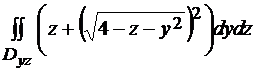 =
=  =0.
=0.
Найдем значение второго слагаемого 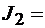
 . Что изменится при вычислении этого интеграла? Здесь интеграл
. Что изменится при вычислении этого интеграла? Здесь интеграл  =
=  , где S3 - половина параболоида с уравнением
, где S3 - половина параболоида с уравнением 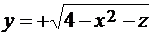 . Нормаль
. Нормаль  к поверхности S3 образует острый угол с осью Oy, S4 - левая часть параболоида, её уравнение:
к поверхности S3 образует острый угол с осью Oy, S4 - левая часть параболоида, её уравнение: 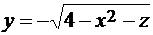 , косинус соответствующего угла между нормалью
, косинус соответствующего угла между нормалью  и осью Oy отрицательный. Половинки параболоида S3 и S4 проектируются на область
и осью Oy отрицательный. Половинки параболоида S3 и S4 проектируются на область  плоскости zx. Граница области состоит из дуги параболы
плоскости zx. Граница области состоит из дуги параболы  и отрезка оси Ox:
и отрезка оси Ox:  .
.
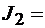
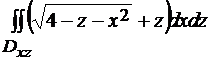 =
=  . Далее следует вычислить двойной интеграл. В результате
. Далее следует вычислить двойной интеграл. В результате 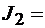 8
8  .
.
Мы вычислили два интеграла из трех. Обсудим приведенное решение. В обоих случаях речь идет о явном задании поверхности. Однако поверхностный интеграл 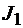 вычисляется по проекции на плоскость yz, а интеграл
вычисляется по проекции на плоскость yz, а интеграл  вычисляется по проекции на плоскость zx. Именно поэтому в первом случае мы выражаем из неявного уравнения параболоида
вычисляется по проекции на плоскость zx. Именно поэтому в первом случае мы выражаем из неявного уравнения параболоида 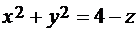 переменную x, т.е. x –это функция от y, z, и плоскость yz – плоскость изменения параметров. А при вычислении
переменную x, т.е. x –это функция от y, z, и плоскость yz – плоскость изменения параметров. А при вычислении  выражаем из уравнения параболоида переменную y как функции. от x, z.
выражаем из уравнения параболоида переменную y как функции. от x, z.
Далее, почему обсуждаем угол между нормалью к поверхности и соответствующей координатной плоскостью и его косинус?
Мы считаем по определению поверхностный интеграл второго рода, сводя его к интегралу первого рода. Например, в случае 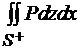 =
=  . Здесь поверхность задана уравнением y=y(x, z), или в параметрической форме x=x, y=y(x, z), z=z. Поэтому координаты векторов
. Здесь поверхность задана уравнением y=y(x, z), или в параметрической форме x=x, y=y(x, z), z=z. Поэтому координаты векторов 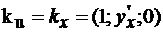 ,
,  . Вычислив координаты вектора
. Вычислив координаты вектора 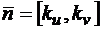 , убедимся в правильности предыдущих результатов.
, убедимся в правильности предыдущих результатов.
И еще один вопрос для обсуждения. Почему нет интеграла по основанию? Действительно, ведь каждый из интегралов является суммой интегралов по поверхности параболоида П и по поверхности К:  , но мы пишем
, но мы пишем 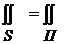 . Почему? Поверхность К – это нижняя часть плоскости z=0, и вектор нормали к ней ортогонален координатным осям Ox и Oy, следовательно косинусы равны нулю и, следовательно,
. Почему? Поверхность К – это нижняя часть плоскости z=0, и вектор нормали к ней ортогонален координатным осям Ox и Oy, следовательно косинусы равны нулю и, следовательно,  = =
= =  = 0.
= 0.
Итак, остался еще один интеграл – последнее слагаемое в основном интеграле  . Здесь
. Здесь  , где П - внешняя сторона параболоида z =4- x 2- y 2, нормаль к которой образует с осью O z острый угол, а К - это часть плоскости z = 0, внешняя нормаль которой образует с осью O z угол
, где П - внешняя сторона параболоида z =4- x 2- y 2, нормаль к которой образует с осью O z острый угол, а К - это часть плоскости z = 0, внешняя нормаль которой образует с осью O z угол  . Понятно, что обе поверхности проектируются в один и тот же круг
. Понятно, что обе поверхности проектируются в один и тот же круг 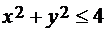 плоскости хОу (поверхность К и есть этот круг. Дальше мы поступаем аналогично разобранному решению, сводя поверхностные интегралы к двойному, при вычислении которого должны получить 8
плоскости хОу (поверхность К и есть этот круг. Дальше мы поступаем аналогично разобранному решению, сводя поверхностные интегралы к двойному, при вычислении которого должны получить 8  .
.
Окончательно,
 = 16
= 16  .
.
Формула Стокса. Пусть S – гладкая (или кусочно-гладкая) поверхность, ограниченная замкнутым контуром L. Будем считать, что мы фиксировали одну из сторон поверхности, выбрав определенное направление вектора нормали (выбрав верхнюю или нижнюю сторону и т.п.). Направление обхода контура L будем считать положительным, если наблюдатель находится на выбранной стороне поверхности и при обходе контура оставляет поверхность слева от себя.
Пусть функции P(x,y,z), Q(x,y,z), R(x,y,z) непрерывно дифференцируемы в некоторой области G, содержащей S. Тогда справедлива формула Стокса:  = =
= =  .
.
Обратите внимание, что для поверхности S, которая является плоской областью, параллельной какой-нибудь координатной плоскости, формула Стокса переходит в формулу Грина. Можно, например, выбрать поверхность, параллельную плоскости xy. У такой поверхности вектор нормали 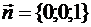 ,
,  (переменная z не меняется) и из формулы Стокса получим формулу Грина
(переменная z не меняется) и из формулы Стокса получим формулу Грина  =
=  .
.
Задача 17.7. Вычислить с помощью формулы Стокса криволинейный интеграл  , где контур L=
, где контур L=  и направление обхода выбрать против хода часовой стрелки, если смотреть из точки (0; 0; 2). В качестве поверхности S взять верхнюю часть сферы, соответствующую
и направление обхода выбрать против хода часовой стрелки, если смотреть из точки (0; 0; 2). В качестве поверхности S взять верхнюю часть сферы, соответствующую  .
.
Решение. Поверхностный интеграл имеет вид 
 . Запишем уравнения поверхности S в параметрической форме
. Запишем уравнения поверхности S в параметрической форме  ,
,  .
.
Для вычисления используем формулу (4.18). Вычислим A, B, C.  .
.
Получим 
 =
= 
Следует заметить, что криволинейный интеграл лучше было бы вычислить непосредственно, поскольку применение формулы Стокса в данном случае приводит к большим вычислениям.
При непосредственном вычислении:
кривая L – окружность, по которой пересекаются сфера и плоскость может быть записана


 ;
; 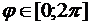 . Тогда
. Тогда  =
=  .
.
Применение формулы Стокса рассматривается здесь только с целью усвоения этой формулы.
Формула Гаусса-Остроградского. Функции  и
и  определены и непрерывны на замкнутой ограниченной области D и
определены и непрерывны на замкнутой ограниченной области D и 

 .
.
Область G=  мы называли элементарной относительно оси Oz. Аналогично можно определить области элементарные относительно осей Ox и Oz. Будем считать, что область G, о которой речь пойдет ниже, можно разбить на конечное число элементарных областей.
мы называли элементарной относительно оси Oz. Аналогично можно определить области элементарные относительно осей Ox и Oz. Будем считать, что область G, о которой речь пойдет ниже, можно разбить на конечное число элементарных областей.
Пусть G  , элементарная область, ограниченная кусочно-гладкой поверхностью S, и функции P(x,y,z), Q(x,y,z), R(x,y,z) и их частные производные
, элементарная область, ограниченная кусочно-гладкой поверхностью S, и функции P(x,y,z), Q(x,y,z), R(x,y,z) и их частные производные  непрерывны в
непрерывны в  . Тогда
. Тогда  =
=  ,
,
где поверхностный интеграл берется по внешней стороне поверхности.
Задача 17.8. Вычислить с помощью формулы Гаусса – Остроградского  , где S- внешняя сторона замкнутой поверхности
, где S- внешняя сторона замкнутой поверхности  , z=0.
, z=0.
Решение. Сделаем предварительные вычисления:  . Поэтому
. Поэтому 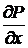 =2x,
=2x,  = 1,
= 1, 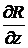 =1. Подставим в формулу:
=1. Подставим в формулу:
 =
=
=  =
=  . Для вычисления тройного интеграла имеет смысл перейти к цилиндрической системе координат. Тогда уравнение параболоида имеет вид
. Для вычисления тройного интеграла имеет смысл перейти к цилиндрической системе координат. Тогда уравнение параболоида имеет вид  , а плоскость, ограничивающая тело снизу, задана z=0. Область изменения параметров
, а плоскость, ограничивающая тело снизу, задана z=0. Область изменения параметров  .
.
 =
=  =
=  .
.
Сделаем замечание: для применения формулы необходимо проверить, что поверхность замкнута, а функции P(x, y, z), Q(x, y, z), R(x, y, z) и их частные производные на поверхности и внутри неё непрерывны.
Элементы теории векторного поля. Пусть G – некоторая область в пространстве R3. Будем говорить, что в области G задано скалярное поле, если каждой точке  поставлено в соответствие некоторое число u(M), т.е. в области G задана числовая функция. Примером такого поля может служить поле температур или поле плотности масс.
поставлено в соответствие некоторое число u(M), т.е. в области G задана числовая функция. Примером такого поля может служить поле температур или поле плотности масс.
Если каждой точке  поставлен в соответствие некоторый вектор
поставлен в соответствие некоторый вектор  (M), то будем говорить, что в области G задано векторное поле. В этом случае в каждой точке задана векторная функция
(M), то будем говорить, что в области G задано векторное поле. В этом случае в каждой точке задана векторная функция  (M). Если в пространстве введена система координат Oxyz, то скалярное и векторное поля становятся функциями координат точек: скалярное поле описывается функцией u= u(x, y, z), а векторное поле –
(M). Если в пространстве введена система координат Oxyz, то скалярное и векторное поля становятся функциями координат точек: скалярное поле описывается функцией u= u(x, y, z), а векторное поле –
векторной функцией  (M) = {P(x;y;z), Q(x;y;z), R(x;y;z)}.
(M) = {P(x;y;z), Q(x;y;z), R(x;y;z)}.
Скалярные и векторные поля называются непрерывными (дифференцируемыми), если непрерывны (дифференцируемы) функции, их задающие.
Градиентом скалярного поля u(x,y,z) называется вектор
grad u=  или grad u=
или grad u=  .
.
Пусть  - единичный вектор, задающий произвольное направление
- единичный вектор, задающий произвольное направление 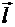 , M – произвольная точка пространства.
, M – произвольная точка пространства.
Производная скалярного поля u в точке M по направлению 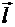 характеризует скорость изменения функции u(M) по заданному направлению и может быть найдена по формуле
характеризует скорость изменения функции u(M) по заданному направлению и может быть найдена по формуле  , где через (
, где через ( ) обозначено скалярное произведение векторов.
) обозначено скалярное произведение векторов.
Введем в рассмотрение векторный символ  , который называют набла или оператор Гамильтона. В системе Oxyz
, который называют набла или оператор Гамильтона. В системе Oxyz  . Тогда вектор градиент можно переписать в виде grad u=
. Тогда вектор градиент можно переписать в виде grad u=  .
.
Дивергенция (расходимость) дифференцируемоговекторного поля  (M) – число, обозначаемое div
(M) – число, обозначаемое div  и в прямоугольной системе координат вычисляемое по формуле div
и в прямоугольной системе координат вычисляемое по формуле div  =
=  =
=  .
.
Ротором дифференцируемоговекторного поля  (M) называют вектор rot
(M) называют вектор rot 
 , где [
, где [  ] – векторное произведение векторов. Для записи и вычисления ротора используют также определитель rot
] – векторное произведение векторов. Для записи и вычисления ротора используют также определитель rot 

 .
.
Пусть  – непрерывное векторное поле в области G, ГAB – кусочно-гладкая кривая в области G. Работой поля
– непрерывное векторное поле в области G, ГAB – кусочно-гладкая кривая в области G. Работой поля  вдоль кривой ГAB называют криволинейный интеграл второго рода
вдоль кривой ГAB называют криволинейный интеграл второго рода  .
.
Если Г – замкнутая кривая (A=B), то этот интеграл называют циркуляцией поля  по кривой Г.
по кривой Г.
Потоком векторного поля  через кусочно-гладкую поверхность S
через кусочно-гладкую поверхность S 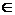 G в направлении вектора нормали
G в направлении вектора нормали  называют поверхностный интеграл
называют поверхностный интеграл  .
.
Векторное поле  (M) называют потенциальным, если его можно представить как градиент некоторого скалярного поля u(M):
(M) называют потенциальным, если его можно представить как градиент некоторого скалярного поля u(M):  = grad u. Саму функцию u(M) называют потенциалом поля
= grad u. Саму функцию u(M) называют потенциалом поля  (M). Если
(M). Если  (M)= (P,Q,R), то
(M)= (P,Q,R), то 

 .
.
Векторное поле  (M) в области G называют соленоидальным, если div
(M) в области G называют соленоидальным, если div  =0.
=0.
Задача 17.9. Найти модуль и направление градиента поля u=x2+2y2+3z2+4xy –3x – 2y – z в точках M1(0, 0, 0), M2(-1, 2, 1). Найти производную по направлению биссектрисы координатного угла xOz в точках M1(0, 0, 0), M2(-1, 2, 1).
Решение. По определению grad u=  . В точке (0, 0, 0)
. В точке (0, 0, 0)
grad u(M1)=(-3; -2; -1), в точке (-1, 2, 1) grad u(M2)=(3; 2; 5).
Модуль (величина) градиента 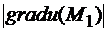 =
=  .
.
Направление градиента определяется единичным вектором  . В точке M1
. В точке M1  .
.
Единичный вектор, задающий направление биссектрисы координатного угла xOz имеет вид  . Производная по направлению
. Производная по направлению 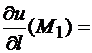
 .
.
Задача 17. 10. Найти дивергенцию векторного поля  ={x; y2; z3} в точке M(-2, 4, 5).
={x; y2; z3} в точке M(-2, 4, 5).
Решение. По определению div  =
=  = 1+2y+3z2. Отсюда div
= 1+2y+3z2. Отсюда div  (M) = 84.
(M) = 84.
Задача 17. 11. Найти ротор векторного поля  ={x2; y2; z3}.
={x2; y2; z3}.
Решение. По определению rot 
 =
=
=i(xz – 3y 2z2) – j(yz – x2) +k(0 – 0).
Окончательно, rot  ={xz – 3y 2z2; –(yz – x2); 0}.
={xz – 3y 2z2; –(yz – x2); 0}.
Задания для самостоятельной работы:
Задача 17. 12. Вычислить значение интеграла  ,
,  ,
,  . Ответ: 7
. Ответ: 7  /3.
/3.
Задача 17. 13. Вычислить значение интеграла  ,
,  ,
,  .
.
Ответ:  (
(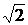 + ln(1+
+ ln(1+ 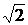 )).
)).
Задача 17. 14. Вычислить значение интеграла  , где 1) S- поверхность сферы
, где 1) S- поверхность сферы  ; 2) S- поверхность конуса
; 2) S- поверхность конуса  .
.
Ответ: 1)  ; 2)
; 2)  .
.
Задача 17. 15. Вычислить 1)  , 2)
, 2) 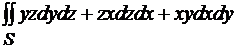 , где
, где
S – внутренняя сторона поверхности тетраэдра  ,
,  .
.
Ответ: 1)  ; 2) 0.
; 2) 0.
Задача 17. 16. Вычислить значение интеграла  , где S верхняя сторона поверхности треугольника
, где S верхняя сторона поверхности треугольника  ,
,  . Ответ: 128/3.
. Ответ: 128/3.
Задача 17. 17. Определить массу, распределенную по поверхности куба 
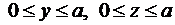 с поверхностной плотностью
с поверхностной плотностью  . Ответ:
. Ответ:  .
.
Задача 17. 18. С помощью формулы Гаусса-Остроградского вычислить  , где S внешняя сторона пирамиды
, где S внешняя сторона пирамиды  ,
,  . Ответ: 3abc/2.
. Ответ: 3abc/2.
Задача 17. 19. С помощью формулы Гаусса-Остроградского вычислить  , где S: 1) внешняя сторона полной поверхности конуса
, где S: 1) внешняя сторона полной поверхности конуса  ,
,  ; 2) внутренняя сторона эллипсоида
; 2) внутренняя сторона эллипсоида  . Ответ: 1)
. Ответ: 1)  ; 2)
; 2)  .
.
18 занятие. Вопросы и задания по темам «Криволинейные интегралы», «Поверхностные интегралы»
1) Сформулируйте определение криволинейного интеграла первого рода и запишите формулы вычисления криволинейного интеграла первого рода.
2) Какие геометрические и физические приложения криволинейного интеграла первого рода вы знаете?
3) Запишите формулу связи между интегралами первого и второго рода.
4) Напишите формулу Грина и сформулируйте условия, при которых она верна.
5) Что означает «Криволинейный интеграл не зависит от пути интегрирования»? Сформулируйте условия независимости.
6) Какие геометрические и физические приложения криволинейного интеграла второго рода вы знаете?
7) Какие способы задания поверхности вы знаете? Для каждого способа приведите пример.
8) Сформулируйте определение поверхностного интеграла первого рода и теорему о вычислении его с помощью двойного интеграла для поверхности, заданной параметрически и явно.
9) Запишите формулы сведения поверхностного интеграла второго рода к двойному для поверхности, заданной параметрически и явно.
10) Напишите формулу Гаусса-Остроградского и сформулируйте условия, при которых она верна.
11) Какие геометрические и физические приложения поверхностных интегралов вы знаете?
12) Вычислить интеграл  , где C – кривая x = t 2,
, где C – кривая x = t 2,  (0 ≤ t ≤ 3).
(0 ≤ t ≤ 3).
13) Вычислить интеграл:  , где C – кривая
, где C – кривая  ,
,  , (0 ≤ t ≤ 2).
, (0 ≤ t ≤ 2).
14) Пусть P =xy, Q=x2/2 – 1/(2-y), G={(x, y), x2 +y2 <4}. Докажите, что выражение Pdx+Qdy является полным дифференциалом некоторой функции u(x, y), найдите эту функцию. Вычислите интеграл  , где A(-1; -2), B(1; 1).
, где A(-1; -2), B(1; 1).
15) Вычислить криволинейный интеграл непосредственно и с помощью формулы Грина:  , P(x,y)= -x2 y, Q(x,y)= xy2, C: окружность
, P(x,y)= -x2 y, Q(x,y)= xy2, C: окружность  .
.
Вопросы для подготовки к экзамену.
1. Функциональные последовательности. Сходимость в точке, на множестве, равномерно, в
среднем квадратичном.
2. Критерий Коши равномерной сходимости.
3. Равномерная сходимость и непрерывность.
4. Равномерная сходимость и интегрирование.
5. Равномерная сходимость и дифференцирование.
6. Функциональные ряды Варианты сходимости.
7. Признаки равномерной сходимости функциональных рядов.
8. Свойства равномерно сходящихся функциональных рядов.
9. Степенные ряды. Теорема Абеля.
10. Радиус сходимости. Формула Коши-Адамара.
11. Дифференцирование и интегрирование степенных рядов.
12. Ряд Тейлора.
13. Основные разложения в степенные ряды
14. Тригонометрическая система. Свойства. Ряд Фурье.
15. Евклидово пространство. Основной пример. Ортонормированные системы. Минимальное свойство коэффициентов Фурье.
16. Неравенство Бесселя. Следствие.
17. Преобразование частичных сумм ряда Фурье. Ядра Дирихле, свойства
18. Теорема о сходимости ряда Фурье для кусочно - дифференцируемой функции.
19. Ядра Фейера, свойства. Теорема Фейера.
20. Теорема Вейерштрасса.
21. Полнота тригонометрической системы. Равенство Парсеваля.
22. Интегралы с параметром. Теоремы о непрерывности.
23. Дифференцирование интеграла по параметру.
24. Теорема о повторном интегрировании.
25. Несобственные интегралы с параметром. Основные понятия.
26. Г-функция и B-функция, свойства
27. Мера Жордана - схема определения.
28. Критерий измеримости.
29. Аддитивность меры Жордана.
30. Теорема о мере графика непрерывной функции.
31. Кратные интегралы; определение, свойства.
32. Сведение кратного интегрирования к повторному.
33. Замена переменных в кратных интегралах. Примеры.
34. Кривые на плоскости н в пространстве. Основные понятия и факты,
35. Криволинейные интегралы 1-го типа. Свойства
36. Криволинейные интегралы 2-го типа Свойства
37. Формула Грина
38. Независимость криволинейного интеграла от пути.
39. Поверхности, способы задания. Нормаль, касательная плоскость.
40. Площадь поверхности.
41. Поверхностные интегралы 1 -го типа Свойства.
42. Поверхностные интегралы 2-го типа Свойства.
43. Формула Гаусса - Остроградского.
44. Элементы теории поля.
Основная рекомендуемая литература
1. Кудрявцев Л.Д. Математический анализ. Т.1,2. - М.: Высшая школа, 1970.
2. Кудрявцев Л.Д., Кутасов А.Д., Чехлов В.И.и др. Сборник задач по математическому анализу. Т. 1-3 Изд 2-е, перераб. и доп. М.: Физматлит, 2003.
3. Демидович Б.П. Сборник задач и упражнений по математическому анализу. М.: Астрель, 2005.
Введение.............................................................................................................................. 2
1. Функциональные последовательности и ряды.......................................................... 4
Занятие 1. Предельная функция функциональной последовательности. Равномерная сходимость функциональных последовательностей............................................................................ 4
Занятие 2. Равномерная сходимость функциональных последовательностей........ 8
Занятие 3. Функциональные ряды. Множество сходимости функционального ряда 11
Занятие 4. Равномерная сходимость функциональных рядов................................ 13
2. Степенные ряды........................................................................................................... 16
Занятие 5. Степенные ряды. Интегрирование и дифференцирование степенных рядов 16
Занятие 6. Ряд Тейлора................................................................................................. 19
3. Ряды Фурье.................................................................................................................... 21
Занятие 7. Разложение периодических функций в ряд Фурье............................... 21
Занятие 8. Задания для подготовки к контрольной работе...................................... 22
4. Интегралы, зависящие от параметра.......................................................................... 23
Занятие 9. Интегралы, зависящие от параметра. Определение и свойства........... 23
Занятие 10. Нахождение множества сходимости несобственного интеграла, зависящего от параметра............................................................................................................................. 26
Занятие 11. Эйлеровы интегралы. Гамма- и бета-функции..................................... 29
5. Кратные интегралы..................................................................................................... 31
12 занятие. Вычисление двойного интеграла с помощью сведения к повторному. Теорема о замене переменных в двойном интеграле.................................................................................... 31
13 занятие. Тройные интегралы. Замена переменных в тройном интеграле. Сферические и цилиндрические координаты в  ................................................................................. 40
................................................................................. 40
14 занятие. Вопросы и задания по теме «Кратные интегралы».............................. 47
6. Криволинейные интегралы первого и второго рода. Поверхностные интегралы. Элементы теории поля.............................................................................................................................. 49
15 занятие. Криволинейный интеграл первого рода. Его свойства и вычисление. Формула Грина............................................................................................................................................... 49
16 занятие. Приложения криволинейных интегралов. Условие независимости криволинейного интеграла второго рода от пути интегрирования........................................................... 55
17 занятие. Поверхностные интегралы. Формула Стокса. Формула Гаусса - Остроградского. Элементы теории векторного поля................................................................................... 60
18 занятие. Вопросы и задания по темам «Криволинейные интегралы», «Поверхностные интегралы»........................................................................................................................... 73
Вопросы для подготовки к экзамену......................................................................... 74






