Занятие. Вычисление двойного интеграла с помощью сведения  к повторному. Теорема о замене переменных в двойном интеграле.

Пусть область }, где y₁(x) и y₂(x) – функции непрерывные на [a, b]. Такую область G называют элементарной относительно оси Oy.

Функция f(x,y) определена и непрерывна в области G.

Если существует в области G двойной интеграл , и при каждом x из [a, b] существует определенный интеграл , тогда существует определенный интеграл  (такой интеграл называется повторным), и справедливо равенство ,    (1.13)

т.е. двойной интеграл равен повторному.

Для области, элементарной относительно оси Ox, т.е.

G={(x, y) }, где x₁(y) и x₂(y) – функции непрерывные на [c;d],

справедлива формула              (2.13)

Задача 12.1. Построить область интегрирования .

Решение. Изменение переменной x определяет на плоскости xy полосу . В этой полосе при каждом значении x переменная y изменяется от y=0 (это значение на оси Ox) до y= (это значение на верхней половине окружности ).

Рис.1

Задача 12.2. Вычислить повторный интеграл .

Решение. Обозначим внутренний интеграл 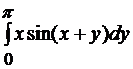через  и вычислим: = = = = = = .

Далее вычисляем интеграл = = 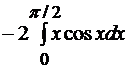. Для его вычисления используем формулу интегрирования по частям: . Перепишем интеграл в виде = = = = = .

Задача 12.3. Вычислить двойной интеграл , D: x=1, y=x², y= .

Решение. Изобразим область интегрирования.

 

Рис. 2

При каждом фиксированном x из [0, 1] переменная y изменяется  от  до  x², т.е. область интегрирования можно представить в виде G={(x, y) }. По формуле (1.13) получим

= .

После того как мы перешли к повторному интегралу, вычислим сначала внутренний интеграл по переменной y, используя формулу Ньютона-Лейбница:

= = = = .

Затем вычислим интеграл по x:

= =

= = .

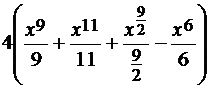
Задача 12.4. Изменить порядок интегрирования: .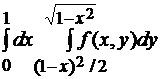

Решение. Кривые y= , y=  и прямая x=0 ограничивают область интегрирования (см. рис 3).

 

Рис. 3

Повторный интеграл равен двойному интегралу по этой области. Для того чтобы поменять пределы интегрирования нужно разбить область на подобласти, каждая из которых описана формулами типа G={(x, y) }, где x₁(y) и x₂(y) – функции непрерывные на [c, d]. 

Кривая y=  является верхней полуокружностью окружности x² +y² =1. Из последнего уравнения выразим x как функцию от y:

x= . Так как нас интересует , то выбираем

x= 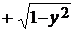. График функции y=  - парабола с вершиной в точке (1, 0). Разрешая это уравнение относительно x, получим два решения это x= . При этом x=  соответствует левой ветви параболы, а x=  - правой ветви. Посмотрим на рисунке. При изменении y от 0 до ½ переменная x меняется в области G₁ от x=  до x= . В области G₂ при изменении y от ½ до 1 переменная x меняется от x=0 (значение на оси Oy)  до x= (значение x на окружности). Поэтому

= + .

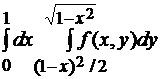Замена переменных в двойном интеграле. Рассмотрим двойной интеграл . Заменить переменные - означает перейти от переменных x и y к новым переменным u и v по формулам x = x(u, v), y=y(u, v),  (u, v) . При этом каждой точке (x, y) области G ставится в соответствие некоторая точка (u, v) , и обратно. Различным точкам соответствуют различные точки, т.е. формулы устанавливают взаимно-однозначное соответствие. Далее, будем считать, что для функций x = x(u, v), y=y(u, v), (u, v)  существуют непрерывные частные производные x_u, x_v, y_u, y_v, и определитель J матрицы , составленной из частных производных (якобиан преобразования) отличен от 0 во всех точках области . Запишем формулу замены переменных в двойном интеграле

= .

Обратите внимание, что под знаком интеграла справа  обозначает модуль якобиана.

В следующей задаче предлагается осуществить переход к полярным координатам, т.е. в качестве переменных u, v выбрать , где - расстояние от точки (x, y) до начала координат, а  - угол, составленный радиус-вектором точки (x, y) с положительным направлением оси Ox.

Задача 12.5.  Переходя к полярным координатам, расставить пределы интегрирования в интеграле  в том и другом порядке D: y x, .

Решение. Область интегрирования изображена на рис. 4.

Рис.4

Формулы, по которым декартовы координаты x и y  выражены через полярные координаты  имеют вид: . Найдем частные производные , составим определитель-якобиан, вычислим его:

= = .

Итак, .

Далее, запишем уравнения окружности  и прямой y=x в полярных координатах:  и  соответственно. Действительно,  из уравнения прямой y=x после подстановки получим , и далее .

Наглядно видно, что при каждом фиксированном значении  координата  меняется от 0 до 3, при этом сама координата  изменяется от  до . И при фиксированном значении  в промежутке от 0 до 3 координата  принадлежит промежутку .

 Таким образом,  = = = .

 

Задача 12.6.  Переходя к полярным координатам, вычислить интеграл , D: .

Решение. Область интегрирования изображена на рис 5.

Рис.5

В качестве промежутка интегрирования по  нужно выбрать отрезок . Действительно, необходимо учесть, во-первых, что область расположена в правой полуплоскости, т.е.   и, во-вторых, условие . Уравнение окружности в полярных координатах запишем в виде: =2cos . Подынтегральная функция равна . Не забывая про якобиан, получим

, где область  задана неравенствами .

Полученный двойной интеграл сводим к повторному .

Вычисляем повторный интеграл, используя формулу Ньютона-Лейбница:

 

=  = = = = .

Рассмотрим задачу, относящуюся к вопросам применения двойных интегралов.

Площадь квадрируемой области D на плоскости (x, y) выражается формулой . Если перейти к новым переменным, то выражение для площади может быть переписано в виде , где  обозначает модуль якобиана преобразования.

Задача 12.7. Найдите площадь фигуры D, ограниченной кривыми: 4y=x² -4x, x=y+3.

Решение.  Первая кривая представляет собой параболу с вершиной в точке (2, -1), вторая – прямая y=x-3. Найдем координаты точек пересечения этих кривых.

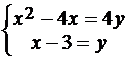. Отсюда получим и .

Область D является элементарной как по Ox так и по Oy, поэтому для сведения к повторному интегралу ее можно представить, например, в виде

{(x, y) }.

= = = =  = = = .

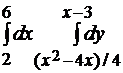Задача 12.8.  Найдите площадь области D, ограниченной кривыми (можно использовать полярные координаты): 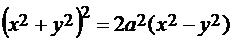,  x² +y²=a², ().

Решение.

Рассмотрим, какую область ограничивают эти кривые. Начнем с более простого. Вторая кривая определяет окружность с центром в начале координат и радиусом a. Рассматриваемая область может находиться как внутри, так и вне этой окружности. Условие в скобках говорит о том, что область D расположена вне окружности. 

Левая часть уравнения 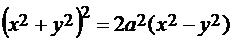 неотрицательна при любых x и y. Поэтому правая часть тоже должна быть неотрицательной, а, значит, . Следовательно, кривая расположена в областях, удовлетворяющих условию , если  или условию , если . График первой кривой симметричен относительно осей Ox и Oy. Действительно, если точка с координатами (x, y) удовлетворяет уравнению, то точки вида (-x, y), (x, - y), (-x, -y) тоже лежат на этой кривой. Таким образом, область ограниченная первой кривой, состоит из четырех одинаковых частей. Поэтому вычисления будем проводить для точек первой четверти. Перейдем к полярным координатам, подставив  в уравнение первой и второй кривых. В первом случае получим . Отсюда  или , причем . С учетом симметрии будем рассматривать часть области, принадлежащей первой четверти. Уравнение окружности в полярных координатах перепишется в виде . Найдем пересечение кривых и . Точка пересечения в первой четверти задана  и . Таким образом, часть области в первой четверти удовлетворяет условиям , .

= = = =  = = .

 

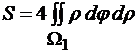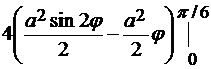Задания для самостоятельной работы:

Задача 12.9. Для заданного множества G записать интеграл  в виде повторных интегралов с разными порядками интегрирования:

1) G – треугольник (2; 1), (6, 2), (4; 6);

2) G – трапеция с вершинами (1; 1), (4; 4), (6; 4), (7; 1);

3) G – область, ограниченная линиями y=-4x+5; y=x²;

4) G – область, ограниченная линиями  x=0, x=1, x=y², y=e^x;

5) G – область, заданная неравенствами ;

Задача 12.10. Изменить порядок интегрирования  в повторных интегралах:

1) ;

2) ;

3) ;

4) ;

5) .

Задача 12. 11. Вычислить повторные интегралы, изменив порядок интегрирования:

1) ;

2) . Ответ: 1) 2;  2) 8.

Задача 12. 12. Вычислить двойные интегралы:

1) , область G ограничена x=-1, x=1, y=x, y=2x;

2) , .   

Ответ: 1) 2ch1-2;  2) 135/4.

Задача 12.12. Перейдите к полярным координатам, а затем сведите интеграл к повторному двумя способами:

1) ;

2) .

3)

13 занятие. Тройные интегралы. Замена переменных в тройном интеграле. Сферические и цилиндрические координаты в

Пусть функция f(x, y, z) определена в области

G={(x, y, z) , }, где y₁(x) и y₂(x) – функции непрерывные на [a, b], а и  определены и непрерывны на множестве

G₁={(x, y) }, которое является проекцией множества G на плоскость xy.

Такую область G называют элементарной относительно оси Oz, а множество G₁ – элементарным относительно оси Oy.

Вычисление тройного интеграла по такой области сводится к вычислению трех однократных интегралов 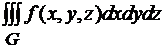.    (1.14)

Задача 13.1.  В повторном интеграле , заменив порядок интегрирования на (z, y, x), расставить пределы интегрирования.   

Решение. Пределы интегрирования в этом примере определяют цилиндр в пространстве R³:

, .

Действительно, неравенства  на плоскости xy задают круг K с центром в начале координат радиуса a, и множество интегрирования может быть представлено в виде {(x, y, z) }. Для расстановки пределов интегрирования в порядке (z, y, x) нужно спроектировать множество интегрирования на плоскость (z, y). Получим прямоугольник, который можно определить неравенствами , . Для каждой фиксированной точки (y, z) из этого прямоугольника переменная x меняется от значения  на левой части цилиндра до  на правой половине.

Поэтому .

Задача 13.2. Интеграл 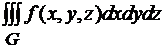 записать в виде повторного интеграла с указанным порядком (x, y, z) (слева направо), если область G ограничена поверхностями z=2(x²+y²) и z=1+x²+y².

Решение. Поверхности z=2(x²+y²) и z=1+x²+y² определяют в пространстве два параболоида. Для того, чтобы спроектировать область G в плоскость xy, нужно исключить переменную z из системы . Получим x²+y²=1, т.е. область G проектируется в круг K. Тогда область G  можно представить в виде: {(x, y, z) }, а следовательно несложно интеграл записать как повторный = .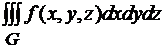

Замена переменных в тройном интеграле. Замена переменных в тройном интеграле аналогично случаю двойного состоит в переходе от переменных x,y,z к новым переменным u,v,w по формулам x = x(u, v,w), y=y(u, v,w), z=z(u, v,w), (u, v, w) . Запишем формулу замены переменных в тройном интеграле

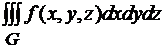= , где 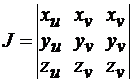 - якобиан отображения области  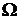в область G.

На формулы замены переменных можно смотреть как на формулы перехода к другой системе координат. Чаще всего мы используем цилиндрические и сферические координаты.

Цилиндрические координаты. Пусть M(x,y,z) произвольная точка пространства R³, а M^’- проекция этой точки на плоскость xy. Точка M может быть однозначно задана тройкой чисел (, z) где

- полярные координаты точки M^’ на плоскости xy, а z – аппликата точки M. Тройка (, z) называется цилиндрическими координатами точки M. Переход от декартовых координат (x,y,z) к цилиндрическим (,z) задается формулами , z=z.                                             (2.14).

Здесь .

Якобиан отображения равен .

 

Сферические координаты. Пусть M(x,y,z) произвольная точка пространства R³, а M^’- проекция этой точки на плоскость xy. Точка M может быть однозначно задана тройкой чисел () где r - расстояние от точки M до начала координат,  - угол, составленный лучами OM и O M^’, а  - полярный угол точки M^’ на плоскости xy. Заметим, что   берется со знаком плюс, если z>0, и со знаком минус, если z<0.

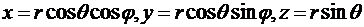Тройка () называется сферическими координатами точки M. Переход от декартовых координат (x,y,z) к сферическим () задается формулами .  (3.14)

Здесь .

Якобиан отображения равен .

Задача 13.3. Вычислить интеграл , если область G ограничена поверхностями z=0 и  (коническая поверхность).  

Решение. Из уравнения  выразим переменную z. Получим z=1 . Нас, конечно, интересует область, ограниченная z=1  (Уравнение z=1  задает неограниченную верхнюю часть конической поверхности).

Эту область интегрирования можно представить в виде

G={(x, y, z) }.

Данный тройной интеграл можно было бы свести к вычислению трех определенных интегралов в декартовых координатах, но удобно сделать замену переменных, перейдя к цилиндрической системе координат. В рассматриваемой области G переменная   меняется от 0 до 2 , при каждом значении  координата  изменяется от 0 до 1, а для каждой точки () переменная z изменяется от 0 (значение z на координатной плоскости xy) до 1  (значение z на конической поверхности). Перепишем подынтегральную функцию в цилиндрических координатах f(x,y,z)= , уравнение конической поверхности в цилиндрических координатах z=1 . Якобиан перехода равен . 

=  = .

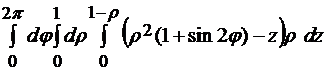Задача 13.4. Вычислить интеграл , перейдя к сферическим координатам, если f(x,y,z)= , область G = . 

Решение. Каждое из уравнений  и 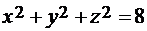 задает сферу с центром в начале координат и радиусом 1 и 2  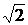соответственно. Перепишем в сферических координатах по формулам (3.14) уравнения сфер, ограничивающих область G. Получим r =1 и r =2  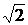соответственно. Таким образом, сферические координаты точек, принадлежащих G, удовлетворяют условию 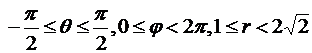. Перепишем подынтегральную функцию в сферических координатах f(x,y,z)= 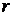. Якобиан отображения равен .

= = .

 

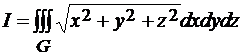Задача 13.5. Вычислить объем тела V, ограниченного заданными поверхностями:

Решение. Объем тела V выражается в декартовых координатах формулой 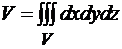. Область V ограничена снизу плоскостью z=0, а сверху – поверхностью параболоида вращения z=4-(x²+y²). Плоскости образуют боковую поверхность V. Можно записать тройной интеграл в виде:

,

где D – множество в плоскости xy, в точки которого проектируется область V. Используя условие задачи, запишем множество D={(x,y,0) }.

= =

Физические приложения кратных интегралов. Приведем некоторые формулы, относящиеся к задачам применения кратных интегралов.

Пусть G – материальная бесконечно тонкая пластинка с плотностью . То есть мы будем говорить о множестве на плоскости xy, которое мы выше называли квадрируемая область (измеримое множество). В каждой точке этого множества определена функция  Справедливы следующие формулы:

a) m =  - масса пластинки;

b) M_x = , M_y =   - статические моменты пластинки относительно осей Ox и Oy;

c)  - координаты центра масс пластинки.

Если V материальное тело в пространстве R³ с плотностью , то справедливы следующие формулы:

d) m =  - масса тела;

e)  M_yz = 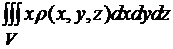, M_zx = ,   

M_xy =   - статические моменты тела относительно координатных плоскостей yz, zx и xy;

f)  - координаты центра масс тела.

g) - ньютоновский потенциал поля тяготения тела V в точке (x₀, y₀, z₀). Здесь r  - расстояние между точками M(x, y, z) и M₀(x₀, y₀, z₀),  - гравитационная постоянная.

Задача 13.6. Найти координаты центра масс однородного тела V с плотностью , ограниченного поверхностями x² =4z, y² =4x, x=1, z=0.

Решение. Для применения формул f) необходимо вначале вычислить массу тела V.

m=  = = .

Далее, = = .

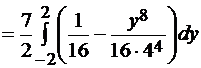Аналогично вычисляем остальные координаты .

Задача 13.7. Найти ньютоновский потенциал поля тяготения однородного шара T радиуса R с плотностью  в точке A, находящейся на расстоянии d от центра шара (d>R).

Решение. Начало системы координат поместим в центр шара, тогда поверхность шара будет задана уравнением x²+y²+z² =R². Точку A разместим на одной из осей, например Oz, тогда ее координаты (0,0,d).  Формула g) вычисления ньютоновского потенциала примет вид:

.

Так как интегрирование ведется по шару, то удобно перейти к сферическим координатам 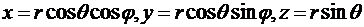, где переменные . Учитывая, что якобиан отображения равен , получим  = . Можно ответ записать короче, заметив, что  - масса шара m.