Вычислите интегралы с параметром
Задача 9.3. 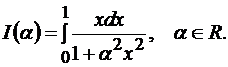 .
.
Решение. Отдельно рассмотрим случаи а)  и б)
и б)  .
.
а) При  интеграл имеет вид:
интеграл имеет вид: 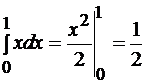 .
.
б) 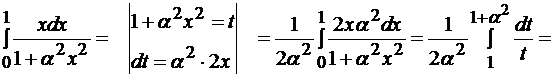
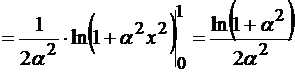 .
.
Ответ: 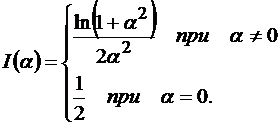
Задача 9.4. 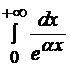 .
.
Решение. Интеграл является несобственным и сходящимся при  .
.
 Ответ:
Ответ: 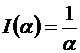 при
при 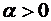 .
.
Задача 9.5. 
Решение. 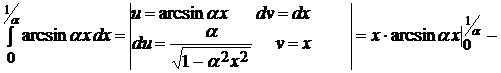

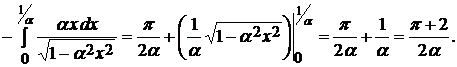
Ответ: 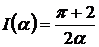 при
при 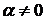 .
.
Задания для самостоятельной работы:
Задача 9.6. Найти 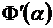 , если
, если  .
.
Занятие 10. Нахождение множества сходимости несобственного интеграла, зависящего от параметра.
Задача 10.1. При каких  интеграл
интеграл 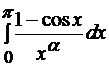 сходится?
сходится?
Решение. Подынтегральная функция имеет особенность в нуле и является неотрицательной. Сравним наш интеграл с интегралом
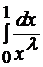 , который сходится при
, который сходится при  . Так как при
. Так как при 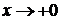 отношение функции
отношение функции 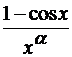 и
и 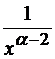 стремится к
стремится к 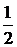 , приходим к выводу: наш интеграл сходится про
, приходим к выводу: наш интеграл сходится про  .
.
Ответ:  сходится при
сходится при  .
.
Задача 10.2. Исследовать на сходимость 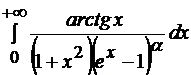 .
.
Решение. Так как интеграл имеет две особенности, разобьем его на два интеграла.
1)  Если
Если 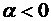 , то интеграл расходится, так как подынтегральная функция положительная и бесконечно большая при
, то интеграл расходится, так как подынтегральная функция положительная и бесконечно большая при 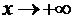 . Если
. Если  , то сходимость интеграла можно доказать, сравнивая его с интегралом вида:
, то сходимость интеграла можно доказать, сравнивая его с интегралом вида:  , который сходится при
, который сходится при 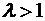 .
.
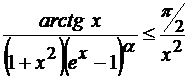 .
.
2) 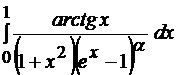 . В зависимости от значения
. В зависимости от значения 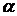 интеграл может быть оказаться обычным интегралом Римана или несобственным.
интеграл может быть оказаться обычным интегралом Римана или несобственным.
Подынтегральная функция имеет особенность в нуле и неотрицательна. Определим функцию эквивалентную ей в нуле.
 ~
~  ~
~  .
.
Интеграл сходится при 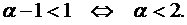
Множество сходимости интеграла 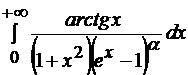 определяется как пересечение промежутков сходимости интегралов 1) и 2).
определяется как пересечение промежутков сходимости интегралов 1) и 2).
Ответ: 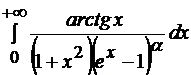 сходится при
сходится при 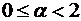 .
.
Задания для самостоятельной работы:
Определите множество сходимости интегралов.
Задача 10.3.  .
.
Задача 10.4. 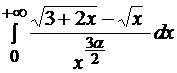 .
.
Исследование несобственных интегралов на равномерную сходимость по параметру.
Интеграл вида  равномерно сходится по параметру
равномерно сходится по параметру 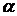 на множестве Y
на множестве Y  неравенство
неравенство 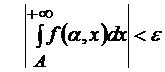 выполнено для
выполнено для 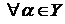 .
.
Задача 10.5. Доказать, что интеграл  является равномерно сходящимся при
является равномерно сходящимся при  .
.
Решение. Воспользуемся признаком Вейерштрасса:
Интеграл 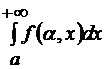 сходится равномерно на множестве Х если:
сходится равномерно на множестве Х если:
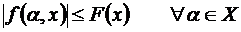 и
и  является сходящимся.
является сходящимся.
 сходится, так как
сходится, так как 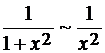 при
при 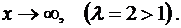
Интеграл является равномерно сходящимся по признаку Вейерштрасса.
Задача 10.6. Самостоятельно докажите равномерную сходимость интеграла  при
при 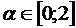 .
.
Задача 10.7. Вычислить  - предельную функцию интеграла
- предельную функцию интеграла 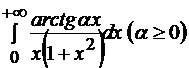 .
.
Решение. Несложно доказать по признаку Вейерштрасса, что интеграл является равномерно сходящимся по параметру.
Найдем производную предельной функции, продифференцировав подынтегральную по 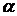 .
. 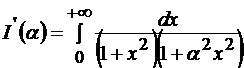 . Вычислим полученный интеграл методом разложения на простые дроби.
. Вычислим полученный интеграл методом разложения на простые дроби.
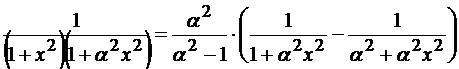 .
.
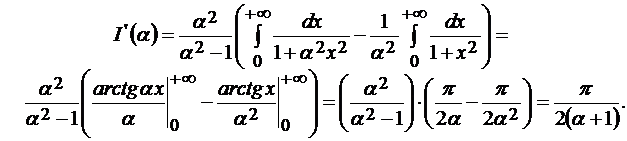
 . Константа
. Константа 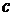 может быть определена из условия:
может быть определена из условия: 
Ответ: 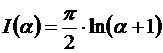 .
.
Задача 10.8. Самостоятельно вычислите предельную функцию интеграла 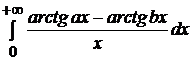 методом интегрирования по параметру.
методом интегрирования по параметру.
Указание:  .
.




