Степенной ряд - это функциональный ряд вида: 
, где 
- это числовая последовательность, называемая общим членом степенного ряда, 
центр степенного ряда. Интервал сходимости степенного ряда имеет вид 
, где 
- радиус сходимости, значение которого может быть вычислено по формуле Коши-Адамара. 
или 
.
Задача 5.1. Найти множество сходимости степенного ряда 
.
Решение. 
, 
. Находим радиус сходимости: 
Интервал сходимости имеет вид 
. Исследуем поведение ряда в граничных точках интервала. При 
имеем числовой ряд 
- знакочередующийся, сходится по признаку Лейбница. При 
ряд имеет вид 
расходящийся гармонический ряд 
.
Множеством сходимости степенного ряда является промежуток 
.
Задача 5.2. Разложить в степенной ряд функцию 
в окрестности точки 0.
Решение. Воспользуемся методом почленного интегрирования степенного ряда: 
. При разложении подынтегральной функции в степенной ряд воспользуемся формулой суммы геометрической прогрессии: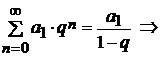 
.
Проинтегрируем почленно полученный степенной ряд.
.
Полученный степенной ряд сходится на отрезке 
.
Задача 5.3. Разложить в степенной ряд функцию 
в окрестности точки -2.
Решение. Воспользуемся методом почленного дифференцирования ряда: 
. а) Разложим в степенной ряд функцию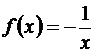 
и б) полученный ряд продифференцируем.
а) 
.
б) 
.
Задача 5.4. Найдите сумму степенного ряда 
.
Решение. Ряд сходится при 
. Для нахождения его суммы проинтегрируем степенной ряд:
.
Задача 5.5. Найдите сумму ряда 
.
Решение. Ряд сходится при 
. Продифференцируем степенной ряд.
.
Задача 5.6. Найдите сумму числового ряда. 
Решение. Данный числовой ряд является значением степенного ряда 
при 
.
.
При значение предельной функции равно 
.
Задания для самостоятельной работы:
Разложите функцию в степенной ряд в окрестности указанной точки.
Задача 5.7. 
Задача 5.8. 
Задача 5.9.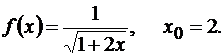 
Суммировать степенные ряды и найти множество сходимости:
Задача 5.10. 
Задача 5.11. 
Задача 5.12. 
Занятие 6. Ряд Тейлора
Бесконечно дифференцируемая в некоторой окрестности точки 
функция представляется степенным рядом Тейлора вида 
. Если 
, то ряд называется рядом Маклорена.
Разложения основных элементарных функций в ряд Маклорена.
1. Показательная функция:
.
2. Тригонометрические функции:
.
.
3. Степенная функция:
, где
.
4. Логарифмическая функция:
.
Задача 6.1. Разложить в ряд Маклорена функцию 
.
Решение. Воспользуемся стандартным разложением степенной функции при 
.
Задача 6.2. Разложить функцию 
в ряд Тейлора в окрестности точки .
Решение. Сделаем замену переменной и воспользуемся разложением Маклорена для показательной функции.
.
Разложить функции в ряд Тейлора в окрестности точки .
Задача 6.3.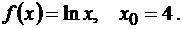 
Задача 6.4. 
Ряды Фурье.
