Введение
Стратегическим направлением модернизации и оптимизации высшего образования является увеличение времени на самостоятельную работу студентов. И это понятно: современные условия диктуют необходимость непрерывного образования, когда от студентов и, в дальнейшем, от выпускников университета требуется постоянное совершенствование знаний. Выпускник должен быть ориентирован на большую инициативу и самостоятельность, должен обладать способностью работать в различных рабочих командах, иметь высокую мотивацию к переобучению.
Одним из основных факторов, обеспечивающих большую эффективность процесса обучения, и позволяющих достигнуть более высокого качества обучения, является сокращение аудиторной нагрузки, замена пассивного слушания лекций возрастанием доли самостоятельной работы студентов. Объем самостоятельной работы студентов определяется ФГОС и учебным планом направления подготовки 010300 «Фундаментальная информатика и информационные технологии».
Дисциплина «Кратные интегралы и ряды» относится к математическому и естественно-научному циклу. Это обязательный курс для студентов 2 курса, читается в 3 семестре. На изучение дисциплины отводится 144 часа, из которых 36 часов лекционных и 36 часов практических занятий. Остальные часы так или иначе связаны с самостоятельной подготовкой. Объем информации по этой дисциплине (полный набор вопросов приведен в приложении) весьма значителен. Отсюда совершенно естественно следует, что большая часть работы переносится на самостоятельную подготовку.
В предлагаемом учебном пособии приводятся методические материалы по дисциплине «Кратные интегралы и ряды»: для каждой темы приведены необходимые теоретические сведения и примеры решения задач, представлены варианты контрольных заданий, приведен список экзаменационных вопросов. Все эти материалы призваны оказать помощь по организации самостоятельной работы, облегчить и оптимизировать внеаудиторную самостоятельную работу.
При подготовке были использованы материалы задачников
Кудрявцев Л.Д., Кутасов А.Д., Чехлов В.И., Шабунин М.И. Сборник задач по математическому анализу. Том 2, 3.
Демидович Б.П. Сборник задач и упражнений по математическому анализу.
Функциональные последовательности и ряды
Занятие 1. Предельная функция функциональной последовательности. Равномерная сходимость функциональных последовательностей
Функциональной последовательностью 
называется последовательность элементами которой являются функции. Если числовая последовательность 
сходится, то говорят, что последовательность функций 
сходится в точке 
.
Последовательность , сходящуюся в каждой точке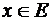 
, называют сходящейся на множестве 
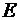. В этом случае на множестве 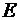определена функция 
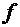, значение которой в точке 
равно пределу последовательности . Эту функцию называют предельной функцией последовательности и пишут 
, .
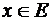Найдите предельную функцию функциональной последовательности:
Задача 1.1.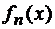 
= 
.
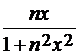Решение. 
.
Задача 1.2. =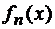 
.
Решение. При вычислении воспользуемся следствием из второго замечательного предела
.
= 
.
Задача 1.3. =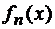 
, 
.
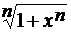Решение. 
Рассмотрим три случая. 
Таким образом: 
Задача 1.4. =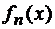 
.
Решение. 
Данный предел может быть вычислен с помощью правила Лопиталя:
Задача 1.5. 
=
Решение. 
Рассмотрим три случая:
при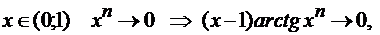 
при 
при 
Окончательно:
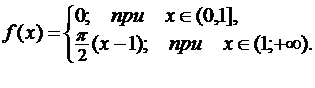
Задача 1.6. =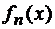 
.
Решение. 
Воспользуемся разложением по формуле Тейлора:
Задача 1.7. =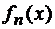 
.
Решение.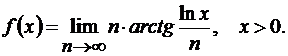 
Воспользуемся заменой на эквивалентную бесконечно малую: 
Задача 1.8. =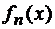 
Решение. 
Сделаем замену переменной 
и воспользуемся правилом Лопиталя:
.
Задача 1.9. = 
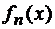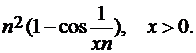
Решение. f(x)= 
Воспользуемся разложением 
по формуле Тейлора: 
.
.
Задача 1.10. =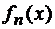 
Решение. f(x)=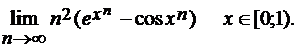 
Так как 
сделаем замену переменной 
и воспользуемся разложением по формуле Тейлора:
Следовательно 
.
Задания для самостоятельной работы:
Задача 1.11.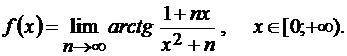 
Задача 1.12.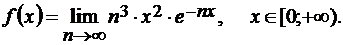 
Задача 1.13. 
Задача 1.14. 
Задача 1.15. 
