Глава 1. Общие положения
1. Учебная программа разработана в соответствии с Государственным общеобязательным стандартом среднего образования (начального, основного среднего, общего среднего образования), утвержденным постановлением Правительства Республики Казахстан от 23 августа 2012 года №1080.
2. Цель обучения – обеспечение качественного усвоения содержания предмета «Геометрия», формирование функциональной грамотности обучающихся, в том числе в интеграции с другими предметами, развитие интеллектуального уровня учащихся на основе общечеловеческих ценностей и лучших традиций национальной культуры.
3. Задачи:
1) способствовать формированию и развитию математических знаний, умений и навыков по подразделам программы: « Понятие о геометрических фигурах », « Взаимное расположение геометрических фигур », « Метрические соотношения », « Векторы и преобразования»;
2) содействовать применению математического языка и основных математических законов, количественных отношений и пространственных форм для решения задач в различных контекстах;
3) направлять знания обучающихся на создание математических моделей с целью решения задач, интерпретировать математические модели, которые описывают реальные процессы;
4) формировать элементарные навыки применения математических методов для исследования и решения задач по физике, химии, биологии и в других теоретических областях и практической деятельности, навыки, необходимые для самостоятельного изучения и продолжения образования в будущей выбранной профессии;
5) развивать логическое и критическое мышление, творческие способности для подбора подходящих математических методов при решении практических задач, оценки полученных результатов иустановления их достоверности;
6) развивать коммуникативные навыки, в том числе способность передавать информацию точно и грамотно, использовать информацию из различных источников, включая публикации и электронные средства;
7) развивать личностные качества, такие, как независимость, ответственность, инициативность, настойчивость, терпение и толерантность, необходимые как для самостоятельной работы, так и для работы в команде;
8) знакомить с историей развития математики, с историей возникновения математических понятий;
9) развивать навыки использования информационно-коммуникационных технологий (ИКТ) в процессе обучения геометрии;
10) обеспечить понимание значимости математики для общественного прогресса.
Глава 2. Организация содержания учебного предмета «Геометрия»
4. Объем учебной нагрузки по учебному предмету «Геометрия» составляет:
1) в 7-ом классе – 2 часа в неделю, 68 часов в учебном году;
2) в 8-ом классе – 2 часа в неделю, 68 часов в учебном году;
3) в 9-ом классе – 2 часа в неделю, 68 часов в учебном году.
5. Базовое содержание учебного предмета геометрии 7 класса включает следующие разделы:
1) «Начальные геометрические сведения».Основные понятия геометрии. Простейшие фигуры геометрии. Аксиома и теорема. Равенство фигур. Доказательство теоремы. Метод доказательства от противного. Смежные и вертикальные углы и их свойства. Биссектриса угла. Перпендикуляр.
2) «Треугольники». Треугольник и его виды. Равенство треугольников. Признаки равенства треугольников. Равнобедренный треугольник. Медиана, биссектриса, высота, средняя линия треугольника.
3) «Взаимное расположение прямых». Углы, образованные при пересечении двух прямых секущей. Признаки параллельности прямых. Свойства параллельных прямых. Сумма углов треугольника. Внешний угол треугольника. Неравенство треугольника. Признаки равенства прямоугольных треугольников. Свойства прямоугольного треугольника. Перпендикулярные прямые. Наклонная и ее проекция. Единственность перпендикуляра к прямой.
4) «Окружность. Геометрические построения». Окружность, круг, их элементы и части. Центральный угол. Взаимное расположение прямой и окружности, двух окружностей. Касательная к окружности. Свойства касательных к окружности. Окружности, описанная и вписанная в треугольник. Задачи на построение.
5) Повторение курса геометрии7 класса.
6. Базовое содержание учебного предмета геометрии 8 класса включает следующие разделы:
1) Повторение курса геометрии7 класса.
2) «Многоугольники. Исследование четырехугольников». Многоугольник. Выпуклый многоугольник. Сумма внутренних углов многоугольника. Внешний угол многоугольника. Сумма внешних углов многоугольника. Параллелограмм и его свойства. Признаки параллелограмма. Прямоугольник, ромб, квадрат, их свойства и признаки. Теорема Фалеса. Пропорциональные отрезки. Трапеция. Равнобедренная и прямоугольная трапеции и их свойства. Средняя линия треугольника. Средняя линия трапеции. Замечательные точки треугольника. Свойство медиан треугольника.
3) «Соотношения между сторонами и углами прямоугольного треугольника». Синус, косинус, тангенс и котангенс острого угла прямоугольного треугольника. Теорема Пифагора. Основное тригонометрическое тождество и его следствия. Значение синуса, косинуса, тангенса и котангенса углов 300, 450, 600. Решение прямоугольных треугольников. Тригонометричекие функции углов  и (
и (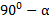 ).
).
4) «Площади». Понятие площади. Равновеликость и равносоставленность фигур. Площади квадрата, прямоугольника, параллелограмма, ромба, треугольника, трапеции.
5) «Прямоугольная система координат на плоскости». Координаты точки на плоскости. Координаты середины отрезка. Расстояние между двумя точками. Уравнение окружности. Уравнение прямой. Взаимное расположение прямых и окружностей, заданных уравнениями. Применение координат к решению задач.
6) Повторение курса геометрии8 класса.
7. Базовое содержание учебного предмета «Геометрия» 9 класса включает следующие разделы:
1) Повторение курса геометрии8 класса.
2) «Векторы на плоскости». Понятие вектора. Нулевой вектор. Единичный вектор. Коллинеарные векторы. Длина (модуль) вектора. Равенство векторов, сложение векторов и его свойства, вычитание векторов, умножение вектора на число. Разложение вектора на плоскости по двум неколлинеарным векторам. Координаты вектора. Действия над векторами в координатной форме. Критерий коллинеарности векторов. Радиус-вектор точки. Связь между координатами точек и векторов на плоскости. Угол между векторами. Скалярное произведение векторов. Применение векторов к решению задач.
3) «Преобразования плоскости».Преобразование плоскости, движение и его свойства. Композиция (произведение) преобразований. Равенство фигур и его свойства. Осевая и центральная симметрия, параллельный перенос, поворот как движение плоскости. Гомотетия, преобразование подобия и его свойства. Подобные фигуры. Признаки подобия треугольников. Подобие прямоугольных треугольников.
4) «Решение треугольников».Теоремы синусов и косинусов. Решение треугольников. Решение задач практического содержания. Формулы для нахождения радиуса окружности с использованием площади вписанных или описанных треугольников.
5) «Окружности. Правильные многоугольники».Вписанный угол и его свойства. Теорема о пропорциональности отрезков хорд и секущих окружности. Свойства вписанных и описанных четырехугольников. Правильные многоугольники и их свойства. Длина дуги окружности. Площадь сектора и сегмента. Формулы, связывающие стороны, периметр, площадь многоугольника и радиусы вписанной и описанной окружностей. Построение правильных многоугольников.
6) Повторение курса геометрия7-9 классов.
8. Содержание учебного предмета включает один раздел: «Геометрия».
9. Раздел «Геометрия» включает следующие подразделы:
1) Понятие о геометрических фигурах;
2) Взаимное расположение геометрических фигур;
3) Метрические соотношения;
4) Векторы и преобразования.
Глава 3. Система целей обучения
10. Цели обучения в программе представлены кодировкой. В коде первое число обозначает класс, второе и третье числа –раздел и подраздел программы, четвёртое число показывает нумерацию учебной цели. Например, в кодировке 7.1.1.4 «7» – класс, «1.1» –раздел и подраздел, «4» – нумерация учебной цели.
11. Обучающийся должен:
| Раздел 1. Геометрия | ||||||||
| 1. Понятие о геометри-ческих фигурах | 7.1.1. | 8.1.1. | 9.1.1. | |||||
| 7.1.1.1 - знать основные фигуры планиметрии: точка, прямая; 7.1.1.2 - знать и применять аксиомы принадлежности точек и прямых; 7.1.1.3 - понимать, чем отличается аксиома оттеоремы;выделять условие и заключение теоремы; 7.1.1.4 - знать методы доказательства теорем: прямой метод и метод «от противного»; 7.1.1.5 - знать определения отрезка, луча, угла, треугольника, полуплоскости; 7.1.1.6 - знать и применять аксиомы измерения отрезков и углов; 7.1.1.7 - знать и применять определение и свойства равныхфигур; 7.1.1.8 - знать и применять аксиомы откладывания отрезков и углов; 7.1.1.9 - знать определения смежных и вертикальных углов; 7.1.1.10 - доказывать и применять свойства вертикальных и смежных углов; 7.1.1.11 - знать аксиому существования треугольника, равного данному; 7.1.1.12 - знать определение медианы, биссектрисы, высоты, серединного перпендикуляра и средней линии треугольника и изображать их; 7.1.1.13 - различать виды треугольников; 7.1.1.14 - знать элементы равностороннего, равнобедренного и прямоугольного треугольников; 7.1.1.15 - сравнивать расположение высот в остроугольном, прямоугольном и тупоугольном треугольниках; 7.1.1.16 - доказывать теорему о сумме внутренних углов треугольника и следствияиз неё; 7.1.1.17 - применять теорему о сумме внутреннихуглов треугольника и следствия из неё при решении задач; 7.1.1.18 - знать определение внешнего угла треугольника и доказывать теорему о внешнем угле треугольника; 7.1.1.19 - применять теорему о внешнем угле треугольника; 7.1.1.20 - знать соотношение между сторонами и углами треугольника и применять его при решении задач; 7.1.1.21 - знать и доказывать признаки равенства треугольников; 7.1.1.22 - применять признаки равенства треугольников при решении задач на вычисление и на доказательство; 7.1.1.23 - применять свойства и признаки равнобедренного треугольника; 7.1.1.24 - применять свойстваравностороннего треугольника при решении задач; 7.1.1.25 - доказывать признаки равенства прямоугольных треугольников; 7.1.1.26 - применять признаки равенства прямоугольных треугольников при решении задач; 7.1.1.27 - применять свойства прямоугольного треугольника; 7.1.1.28 - знать определения окружности икруга, их элементов (центр, радиус, диаметр, хорда); 7.1.1.29 - знать и применять определение и свойства центрального угла; 7.1.1.30 - доказывать и применять теоремы о перпендикулярности диаметра и хорды; 7.1.1.31 - знать определение геометрического места точек; 7.1.1.32 - знать понятие о перпендикуляре; | 8.1.1.1 - знать определения многоугольника, выпуклого многоугольника,элементов многоугольника; 8.1.1.2 - выво- дить формулы суммы внутренних углов и суммы внешних углов многоугольника; 8.1.1.3 - знать определение параллелограмма, 8.1.1.4 - выво- дить и применять свойства параллелограмма; 8.1.1.5 - выво- дить и применять признаки параллелограмма; 8.1.1.6 - знать определения прямоугольника, ромба и квадрата, выводить их свойства и признаки; 8.1.1.7 - знать и применять теорему Фалеса; 8.1.1.8 - знать и применять теорему о пропорциональных отрезках; 8.1.1.9 - делить отрезок на nравных частей с помощью циркуля и линейки; 8.1.1.10 - строить пропорциональные отрезки; 8.1.1.11 - знать определение, виды и свойстватрапеции; 8.1.1.12 - доказывать и применять свойство средней линии треугольника; 8.1.1.13 - доказывать и применять свойство средней линии трапеции;
| 9.1.1.1 - выводить и применять формулу длины дуги; 9.1.1.2 - выводить и применять формулу площади сектора, сегмента; 9.1.1.3 - знать определение вписанного угла и его свойства; 9.1.1.4 - знать и применять теоремы о пропорциональности отрезков в круге | ||||||
| 2. Взаимноерасполо-жениегеометри-ческих фигур | 7.1.2. | 8.1.2. | 9.1.2. | |||||
| 7.1.2.1 - знать и применять аксиомы расположения точек на прямой и на плоскости (аксиома порядка); 7.1.2.2 - знать аксиому параллельности прямых; 7.1.2.3- распознавать углы, образованныепри пересечении двух прямых секущей; 7.1.2.4 - доказывать признаки параллельности прямых; 7.1.2.5 - применять признаки параллельности прямых при решении задач; 7.1.2.6 - доказывать свойства параллельных прямых; 7.1.2.7 - применять свойства параллельных прямых при решении задач; 7.1.2.8 - усвоить понятие перпендикуляра, наклонной и проекции наклонной; 7.1.2.9 - доказывать и применять теорему о единственности перпендикуляра к прямой; 7.1.2.10 - знать и применять свойства перпендикулярных прямых; 7.1.2.11 - знатьопределения касательной и секущей к окружности; 7.1.2.12 - анализировать случаи взаимного расположения прямой и окружности, двух окружностей; 7.1.2.13 - знать и применять свойства касательной к окружности при решении задач; 7.1.2.14 - знатьопределения окружностей, вписанной в треугольник и описанной околотреугольника; 7.1.2.15 - объяснять расположениецентров окружностей,вписанной в треугольник и описанной около треугольника; 7.1.2.16 - строить угол, равный данному, биссектрису угла, делить отрезок пополам; 7.1.2.17 - строить серединный перпендикуляр к отрезку, прямую, перпендикулярную к данной прямой; 7.1.2.18 - строить треугольник по заданным элементам; | 9.1.2.1 - знать и применять свойства и признаки вписанных и описанных четырёхугольников; 9.1.2.2 - знать определение и свойства правильных многоугольников; 9.1.2.3 - строить правильные многоугольники; 9.1.2.4 - знатьи применять связь междурадиусами вписанной и описанной окружностей правильного многоугольника; 9.1.2.5 - знатьи применять формулы, связывающие стороны, периметр, площадь правильного многоугольника и радиусывписанной и описанной окружностей правильного многоугольника; 9.1.2.6 - знать и применять свойства медиан треугольника; | |||||||
| 3.Метри- ческие соотноше- ния | 7.1.3. | 8.1.3 | 9.1.3. | |||||
| 7.1.3.1 - знать и применять неравенство треугольника;
| 8.1.3.1 - знать и применять свойства медиан, биссектрис, высот и серединных перпендикуляров к сторонам треугольника; 8.1.3.2 - знать определениясинуса, косинуса, тангенса и котангенса углов через отношения сторон в прямоугольном треугольнике; 8.1.3.3 - доказывать и применять теорему Пифагора; 8.1.3.4 - доказыватьи применять свойства высоты в прямоугольном треугольнике, опущенной из вершины прямого угла на гипотенузу; 8.1.3.5 - строить угол по известному значению его синуса, косинуса, тангенса или котангенса; 8.1.3.6 - использовать прямоугольный треугольник для вывода значений синуса, косинуса, тангенса и котангенса углов 300, 450, 600; 8.1.3.7 - применять значения синуса, косинуса, тангенса и котангенса углов 300, 450, 600 для нахождения элементов прямоугольного треугольника; 8.1.3.8 - находить стороны и углы прямоугольного треугольника по двум заданным элементам; 8.1.3.9 - знать определение площади многоугольника и ее свойства; 8.1.3.10 - знать определения равновеликих и равносоставленных фигур; 8.1.3.11 - выводить и применять формулыплощади параллелограмма, ромба; 8.1.3.12 - выводитьи применять формулы площади треугольника; 8.1.3.13 - выводить и применять формулы площади трапеции; 8.1.3.14 - вычислять расстояние между двумя точками на плоскостипо их координатам; 8.1.3.15 - находить координаты середины отрезка; 8.1.3.16 - находитькоординаты точки, делящей отрезок в заданном отношении; 8.1.3.17 - знать уравнение окружности с центром в точке (a,b) и радиусом r:
8.1.3.18 - строить окружность по заданному уравнению; 8.1.3.19 - записывать общее уравнение прямой и уравнение прямой, проходящей через две заданные точки:
8.1.3.20 - решение простейших задач в координатах; 8.1.3.21 - выводить формулу 8.1.3.22 - выводить и применять основные тригонометрические тождества; 8.1.3.24 - находить значения
| 9.1.3.1 - находить координаты вектора;
9.1.3.2 - находить длину вектора;
9.1.3.3 - выпол-
нять действия над векторами в координатах;
9.1.3.4 - знать и применять скалярное произведение векторов и его свойства;
9.1.3.5 – вычис-
лять угол между векторами;
9.1.3.6 - знать и применять теорему косинусов;
9.1.3.7 - знатьи применять теорему синусов;
9.1.3.8 - знать и применять формулы площади вписанного треугольника (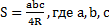 - стороны треугольника, R-радиус описанной окружности), площади описанного многоугольника
( - стороны треугольника, R-радиус описанной окружности), площади описанного многоугольника
(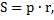 где где  – радиус вписанной окружности, – радиус вписанной окружности,  - полупериметр многоугольника);
9.1.3.9 - знать и применять формулы для нахождения радиуса окружности, используя площади вписанных и описанных треугольников;
9.1.3.10 - при-
менять теоремы синусов и косинусов для решения треугольников и прикладных задач; - полупериметр многоугольника);
9.1.3.9 - знать и применять формулы для нахождения радиуса окружности, используя площади вписанных и описанных треугольников;
9.1.3.10 - при-
менять теоремы синусов и косинусов для решения треугольников и прикладных задач;
| ||||||
| 4. Векторы и преобразо- вания | 7.1.4. | 8.1.4. | 9.1.4. | |||||
|
| 9.1.4.1 - знать определения вектора, коллинеарных векторов, равных векторов, нулевого вектора, единичного вектора и длины вектора; 9.1.4.2 - знать и применять правила сложения векторов и умножения вектора на число; 9.1.4.3 - применять условие коллинеарности векторов; 9.1.4.4 - раскладывать вектор по двум неколлинеарным векторам; 9.1.4.5 - знать определение угла между двумя векторами; 9.1.4.6 - находить скалярное произведение векторов; 9.1.4.7 - решатьзадачи векторным методом; 9.1.4.8 - знать виды, композициидвижений иих свойства; 9.1.4.9 - строить образы фигур при симметриях, параллельном переносе, повороте; 9.1.4.10 - решать задачи с применениемпреобразований плоскости; 9.1.4.11 - знать определение и свойства гомотетии; 9.1.4.12 - строить образы различных фигур при гомотетии; 9.1.4.13 - знать определение и свойства подобных фигур; 9.1.4.14 - знать и применять признаки подобия треугольников; 9.1.4.15 - знать и применять подобие прямоугольных треугольников; 9.1.4.16 - знать и применять свойство биссектрисы треугольника; 9.1.4.17 - знать формулу зависимости между площадями подобных фигур и коэффициентом подобия; 9.1.4.18 - знать симметрии правильных многоугольников; 9.1.4.19 - применять векторы к решению задач. | |||||||
12. Настоящая учебная программа реализуется в соответствии с Долгосрочным планом к Типовой учебной программе по учебному предмету «Геометрия» для 7-9 классов уровня основного среднего образования по обновленному содержанию.
13. Распределение часов в четверти по разделам и внутри разделов варьируется по усмотрению учителя.
Приложение
к Типовой учебной программе
по учебному предмету «Геометрия»
для 7-9 классов уровня основного
среднего образования по
обновленному содержанию
Долгосрочный планпо реализации Типовой учебной программы





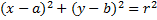 ;
;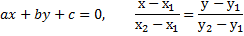
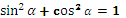 , используя теорему Пифагора и применять при решении задач;
, используя теорему Пифагора и применять при решении задач;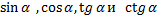 по данному значению одного из них;
по данному значению одного из них;
