Найти:
0) фазу колебания;
2) модуль скорости;
3) модуль ускорения;
4) длину волны.
| 0 | 2 | 3 | 4 |
| 1,05 | 1,05×10-2 | 1,90×10-2 | 180 |
В А Р И А Н Т 17
|
 |
1) начальную фазу в радианах;
2) амплитуду колебаний.
В момент времени t = 4 с найти:
4) кинетическую энергию точки;
5) потенциальную энергию точки.
| 1 | 2 | 4 | 5 |
| 3,14 | 0,255 | 2×10-4 | 0 |
Точка участвует в двух колебаниях одного направления одинаковой частоты 2 Гц. Амплитуды: А1 = 5 см, А2 = 3 см, начальные фазы: j1 = 00,
j2 = - 900.
Найти:
6) координату точки в начальный момент (в см);
9) в какой момент координата будет впервые иметь значение -5 см?
| 6 | 9 |
| 5 | 0,25 |
Уравнение колебаний имеет вид:
Х = 0,1 × sin 
×t м.
Скорость распространения колебаний 300 м/с. Написать уравнение волны и для точки, отстоящей на расстоянии 600 м от источника колебаний в момент времени 4 с найти:
0) смещение от положения равновесия;
1) скорость;
3) фазу колебания;
5) длину волны.
| 0 | 1 | 3 | 5 |
| 0 | - 0,157 | 3,14 | 1,2×103 |
В А Р И А Н Т 18
 |
График зависимости ускорения от времени для колеблющейся точки массой 5 г имеет вид
Найти в момент времени t = 2 с:
7) величину смещения точки от положения равновесия;
8) величину скорости;
9) величину возвращающей силы.
| 7 | 8 | 9 |
| 4,056×10-2 | 0 | 5×10-4 |
Точка участвует одновременно в колебаниях вдоль осей Х и Y:
Х = 10 × sin (200 pt) см
Y = -20 × cos (200 pt) см.
Найти:
7) минимальное удаление точки от начала координат (в см);
8) какой угол (в градусах) составляет вектор скорости с осью Х в момент времени t = 0?
9) Какова скорость точки в этот момент?
| 7 | 8 | 9 |
| 10 | 0 | 62,8 |
Волна с периодом 2 с и амплитудой 0,04 м распространяется со скоростью 300 м/с. Написать уравнение волны и для точки, отстоящей от источника колебаний на расстоянии 75 м в момент времени 0,5 с после начала колебаний найти:
1) модуль скорости;
2) модуль ускорения;
3) фазу колебания;
4) длину волны.
| 1 | 2 | 3 | 4 |
| 0,0889 | 0,279 | 0,785 | 600 |
В А Р И А Н Т 19
По графику колебаний точки массой 5 г найти:
7) кинетическую энергию точки в момент времени t = 2 с;
8) полную энергию точки;
9) величину максимальной возвращающей силы.
| 7 | 8 | 9 |
| 1,5405×10-5 | 1,5405×10-5 | 6,1625×10-4 |
Точка участвует в двух однонаправленных колебаниях с частотой
200 Гц, причем А1 = 10 см, А2 = 5 см, j1 = 900, j2 = 1800.
Найти:
7) координату точки при t = 0 (в см);
9) в какой момент времени координата будет впервые иметь значение 10 см?
| 7 | 9 |
| -5 | 3,75×10-3 |
Волна с периодом 1,2 с и амплитудой колебаний 2 см распространяется со скоростью 15 м/с. Написать уравнение бегущей волны и для точки, находящейся на расстоянии 45 м от источника волны через 4 с от начала колебаний найти:
0) фазу колебания;
1) модуль смещения от положения равновесия;
2) модуль скорости;
3) модуль ускорения;
4) длину волны.
| 0 | 1 | 2 | 3 | 4 |
| 5,24 | 1,73×10-2 | 5,24×10-2 | 0,474 | 18 |
В А Р И А Н Т 20
Зависимость ускорения от времени для колеблющейся точки массой 10 г имеет вид:
|
 |
Найти:
6) начальную фазу колебаний в радианах;
8) величину максимальной возвращающей силы;
9) потенциальную энергию в момент времени t = 4 с.
| 6 | 8 | 9 |
| 1,57 | 10-3 | 2,028×10-5 |
Точка участвует в колебаниях вдоль осей Х и Y:
Х = 5 × cos (100 pt) см
Y = 3 × sin (100 pt) см.
Найти:
7) минимальное удаление точки от начала координат (в см);
8) в какой момент времени точка впервые пройдет это положение?
9) чему равен модуль скорости точки в этот момент (в м/с)?
| 7 | 8 | 9 |
| 3 | 0,005 | 15,70 |
Уравнение колебаний источника имеет вид:
Х = 3 × sin 20 pt см.
Скорость распространения волны 200 м/с. Написать уравнение бегущей волны и для точки, находящейся на расстоянии 5 м от источника колебаний через 0,1 с после начала колебаний найти:
0) период колебаний;
1) фазу колебаний;
4) ускорение;
5) длину волны.
| 0 | 1 | 4 | 5 |
| 0,1 | 4,71 | 118 | 20 |
В А Р И А Н Т 21
Используя график зависимости ускорения колеблющейся точки от времени, найти:
a,см/с2
Найти в момент времени t = 4 с:
3) фазу колебания в градусах;
4) величину смещения точки от положения равновесия;
5) скорость точки.
| 3 | 4 | 5 |
| 270 | 8,113×10-2 | 0 |
Точка участвует в двух колебаниях одного направления с периодами 1 с, причем А1 = А2 = 5 см, j1 = 00, j2 = 900.
Найти:
6) максимальное значение координаты точки (в см);
7) минимальное (по модулю) значение координаты (см);
8) в какой момент времени координата в первый раз примет это минимальное значение?
9) Какова координата точки через 1,5 с после начала колебаний? Ответ выразить в сантиметрах.
| 6 | 7 | 8 | 9 |
| 7,07 | 0 | 0,125 | -5 |
Уравнение колебаний имеет вид:
Х = 0,02 × sin 
×t м.
Скорость распространения колебаний 600 м/с. Написать уравнение бегущей волны и для точки, отстоящей от источника волн на расстоянии 75 м через 1,125 с после начала колебаний найти:
0) фазу колебания;
3) ускорение;
5) длину волны.
| 0 | 3 | 5 |
| 1,05 | -1,9×10-2 | 3 600 |
В А Р И А Н Т 22
Частица массой 10 г совершает колебания согласно графику:
 |
Найти в момент времени t = 4 с:
0) величину возвращающей силы;
1) полную энергию;
4) момент времени, когда модуль ускорения впервые достигает максимума.
| 0 | 1 | 4 |
| 0 | 2,776×10-6 | 2 |
Точка участвует в двух колебаниях одного направления с частотой 100 Гц, причем А1 = 5 мм, А2 = 2 мм, j1 = 00, j2 = 900.
Найти:
8) координату точки в начальный момент (в мм);
9) в какой момент координата будет впервые равна -2 мм?
| 8 | 9 |
| 5 | 2,5×10-3 |
Поперечная волна распространяется в упругой среде со скоростью 26 м/с, период колебаний точек среды 2 с, амплитуда 0,03 м. Для точки, отстоящей на расстоянии 78 м от источника волн в момент времени 3,5 с, найти:
0) фазу колебаний;
2) модуль скорости;
3) модуль ускорения;
4) длину волны;
5) расстояние между ближайшими точками волны, колеблющимися в противофазе.
| 0 | 2 | 3 | 4 | 5 |
| 1,57 | 0 | 0,296 | 52 | 26 |
В А Р И А Н Т 23
Для частицы массой 5 г график зависимости скорости от времени имеет вид:
 |
Найти:
0) частоту колебаний;
1) амплитуду;
2) начальную фазу в радианах.
| 0 | 1 | 2 |
| 0,25 | 0,0637 | 3,14 |
Точка участвует в двух однонаправленных колебаниях с частотой
100 Гц, причем А1 = 2 мм, А2 = 4 мм, j1 = - 900, j2 = 00.
Найти:
6) координату точки при t = 0 (в мм);
7) в какой момент координата будет впервые равна - 4 мм?
8) Какова амплитуда колебаний (в мм)?
9) В какой момент будет достигнуто впервые амплитудное значение Х?
| 6 | 7 | 8 | 9 |
| 4 | 0,005 | 4,472 | 7,341×10-4 |
Уравнение колебаний имеет вид:
Х = 0,01 × sin 2,5 pt м.
Скорость распространения плоской волны 100 м/с. Написать уравнение волны. Для точки, находящейся на расстоянии 20 м от источника колебаний через 1 с после начала колебаний найти:
1) фазу колебания;
4) ускорение;
5) длину волны.
| 1 | 4 | 5 |
| 6,28 | 0 | 80 |
В А Р И А Н Т 24
По графику колебаний материальной точки массой 3 г определить:
6) начальную фазу колебаний в радианах;
7) циклическую частоту;
8) величину максимальной возвращающей силы.
 |
| 6 | 7 | 8 |
| 1,57 | 1,57 | 1,479×10-4 |
Точка участвует во взаимно-перпендикулярных колебаниях:
Х = 5 × sin (200 pt) см
Y = 10 × cos (200 pt) см.
Найти:
7) максимальное удаление точки от начала координат (в см);
8) минимальное удаление (в см);
9) в какой момент впервые достигается минимальное удаление?
| 7 | 8 | 9 |
| 10 | 5 | 2,5×10-3 |
Поперечная волна распространяется вдоль упругого шнура со скоростью 45 м/с, период колебаний точек шнура 1 с, амплитуда 0,05 м. Написать уравнение бегущей волны и для точки, отстоящей на расстоянии 90 м от источника волны в момент времени 2,5 с найти:
0) фазу колебания;
1) модуль смещения точки от положения равновесия;
3) модуль ускорения;
4) длину волны.
| 0 | 1 | 3 | 4 |
| 3,14 | 0 | 0 | 45 |
В А Р И А Н Т 25
Математический маятник, колеблющийся с амплитудой 2 см, обладает энергией 9,86×10-6 Дж. Масса маятника 5 г.
Найти:
0) частоту колебаний;
1) длину маятника;
2) максимальную скорость колебаний маятника. (Принять g = p2).
| 0 | 1 | 2 |
| 0,5 | 1 | 6,28×10-2 |
Точка участвует в двух однонаправленных колебаниях вдоль оси Х с частотой 20 Гц, причем А1 = 3 см, А2 = 4 см, j1 = 900, j2 = 1800.
Найти:
7) максимальное смещение точки от положения равновесия (в см);
8) координату точки при t = 0 (в см);
9) в какой момент координата впервые будет равна 4 см?
| 7 | 8 | 9 |
| 5 | - 4 | 2,5×10-2 |
Уравнение плоской звуковой волны:
x = 6×10-6 cos (1900 t + 5,72 L) м.
Найти:
0) частоту колебаний;
1) длину волны;
2) скорость ее распространения;
3) расстояние между ближайшими точками волны, колеблющимися в противофазе.
| 0 | 1 | 2 | 3 |
| 302 | 1,10 | 332 | 0,55 |
В А Р И А Н Т 26
Используя график зависимости ускорения колеблющейся точки от времени, найти:
 |
Найти в момент времени 2 с:
4) фазу колебаний в радианах;
5) смещение точки от положения равновесия (модуль);
6) скорость точки.
| 4 | 5 | 6 |
| 4,71 | 0,04056 | 0 |
Точка участвует во взаимно-перпендикулярных колебаниях:
Х = 10 × cos (20 pt) см
Y = 5 × sin (20 pt) см.
Найти:
7) максимальное удаление точки от начала координат (в см);
8) в какой момент времени точка будет впервые двигаться по направлению, противоположному оси Х?
9) Чему равен модуль скорости в этот момент?
| 7 | 8 | 9 |
| 10 | 0,025 | 6,28 |
Уравнение колебаний имеет вид:
Х = 0,05 sin 
×t м.
Скорость распространения колебаний 100 м/с. Написать уравнение бегущей волны и для точки, отстоящей от источника колебаний на расстоянии 25 м в момент времени 2,25 с после начала колебаний.
Найти:
0) фазу колебания;
1) ускорение;
2) период колебания;
3) длину волны.
| 0 | 1 | 2 | 3 |
| 1,57 | -3,08×10-2 | 8 | 800 |
В А Р И А Н Т 27
На рисунке представлен график зависимости ускорения от времени для частицы массой 5 г.
Найти:
0) циклическую частоту;
1) амплитуду колебаний.
|
Найти также в момент времени 2 с:
3) кинетическую энергию частицы;
4) ее потенциальную энергию.
| 0 | 1 | 3 | 4 |
| 1,57 | 4,056×10-2 | 0 | 1,014×10-5 |
Точка участвует во взаимно-перпендикулярных колебаниях:
Х = 4 × sin (100 pt) см
Y = -3 × sin (100 pt) см.
Найти:
5) амплитуду колебаний (в см);
7) в какой момент времени смещение будет впервые равно 2 см.
| 5 | 7 |
| 5 | 1,31×10-3 |
Уравнение колебаний имеет вид:
Х = 0,02×sin pt м.
Скорость распространения плоской волны 50 м/с. Написать уравнение бегущей волны и для точки, находящейся на расстоянии 100 м от источника колебаний в момент времени 2,5 с после начала колебаний найти:
0) фазу колебания;
1) смещение точки от положения равновесия;
2) ускорение;
3) расстояние между ближайшими точками волны, колеблющимися в противофазе.
| 0 | 1 | 2 | 3 |
| 1,57 | 0,02 | 0,197 | 50 |
В А Р И А Н Т 28
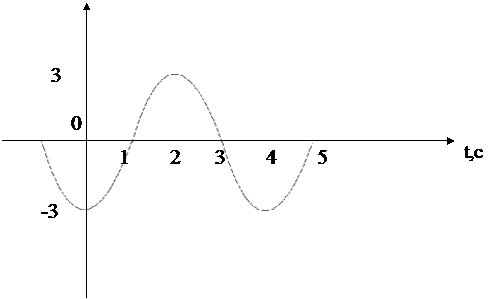Тело массой 10 г совершает колебания по закону, представленному на графике:
В момент времени 3 с найти:
6) фазу колебаний в радианах;
8) кинетическую энергию тела;
9) его полную энергию.
| 6 | 8 | 9 |
| 3,14 | 1,109×10-5 | 1,109×10-5 |
Точка участвует в двух взаимно-перпендикулярных колебаниях:
Х = 4 × sin (200 pt) см
Y = 3 × cos (200 pt) см.
Найти:
4) максимальное смещение точки от начала координат (в см);
5) в какой момент оно достигается впервые? Ответ дать в миллисекундах.
6) Какой угол (в градусах) образует вектор скорости с осью Y в этот момент?
| 4 | 5 | 6 |
| 4 | 2,5 | 180 |
Поперечная волна распространяется в упругой среде со скоростью 39 м/с, период колебаний точек среды 4 с, амплитуда 0,05 м. Для точки, отстоящей на расстоянии 19,5 м от источника волн в момент времени 1,5 с найти:
0) фазу колебания;
1) модуль ускорения;
2) длину волны;
3) расстояние между ближайшими точками волны, колеблющимися в одной фазе.
| 0 | 1 | 2 | 3 |
| 1,57 | 0,123 | 156 | 156 |
В А Р И А Н Т 29
По графику зависимости скорости частицы от времени найти:
6) начальную фазу в радианах;
7) амплитуду колебаний;
8) модуль ускорения частицы в момент времени t = 4 с.
| 6 | 7 | 8 |
| 3,14 | 0,255 | 0 |
Точка участвует в двух колебаниях одного направления, причем
А1 = 5 см, А2 = 3 см, j1 = 1800, j2 = - 900.
Найти:
8) координату точки в начальный момент (в см);
9) амплитуду колебаний (в см).
| 8 | 9 |
| - 5 | 5,83 |
Уравнение плоской волны:
x = 0,04×sin (94,2 t – 63 L) м.
Найти:
0) частоту колебания;
1) период колебания;
2) длину волны;
3) скорость ее распространения;
4) расстояние между ближайшими точками волны, колеблющимися в одинаковых фазах.
| 0 | 1 | 2 | 3 | 4 |
| 15 | 0,667 | 0,10 | 1,5 | 0,10 |
В А Р И А Н Т 30
По графику зависимости ускорения конца ножки камертона от времени найти:
0) циклическую частоту колебаний камертона;
1) амплитуду колебаний конца ножки;
2) максимальный угол (в радианах) отклонения ножки от положения
равновесия, если ее длина 10 см. Ножку в процессе колебаний считать прямой.
| 0 | 1 | 2 |
| 1000 | 4×10-6 | 4×10-5 |
Точка участвует в двух колебаниях одного направления с частотой 20 Гц, причем А1 = А2 = 3 см, j1 = 900, j2 = 1800.
Найти:
7) амплитуду колебаний (в см);
8) координату точки в начальный момент (в см);
9) в какой момент координата будет впервые равна 3 см?
| 7 | 8 | 9 |
| 4,24 | - 3 | 2,5×10-2 |
Волна с периодом 1,6 с и амплитудой колебания 3 см распространяется со скоростью 25 м/с. Написать уравнение бегущей волны и для точки, находящейся на расстоянии 75 м от источника волны через 3,8 с после начала колебаний найти:
0) фазу колебания;
1) модуль смещения от положения равновесия;
2) модуль ускорения;
3) длину волны.
| 0 | 1 | 2 | 3 |
| 3,14 | 0 | 0 | 40 |
